Displacement

Section 4.2 Displacement

One of the characteristics of a moving object is that its position changes with time. The position of a point particle traces out a trajectory in space as it moves from one point to the next. To describe this change, we define a quantity called the displacement vector or simply displacement. Displacement gives overall movement of an object between two instants in time as illustrated in Figure 4.6.

An arrow from \(i\) to \(f\text{.}\) — Figure 4.6. A displacement vector from point labeled \(i\) to another point labeled \(f\text{.}\)

We can write displacement vector in terms of the position vectors of the initial and final points. Let \(\vec r_i\) be the position at when the particle is at \(i\) and \(\vec r_f\) when at \(f\text{.}\) From the vector triangle \(Oif\) in Figure 4.7, it is clear that \(\vec r_i + \Delta \vec r \) equals \(\vec r_f \text{,}\) since both take you from \(O \) to the final location. Therefore, displacement vector, \(\Delta \vec r\) will be

\begin{equation} \Delta \vec r = \vec r_f - \vec r_i. \tag{4.10} \end{equation}

An important thing to note about the displacement vector is that it does not depend on physical location of the origin since the subtraction in \(\vec r_f - \vec r_i\) cancels the location of the starting point for each vector out.

Figure 4.7. Displacement vector, \(\Delta \vec r\text{,}\) and the position vectors \(\vec r_i\) and \(\vec r_f\text{.}\)

It is easier to do the algebra of subtraction using the coordinate representations of the two position vectors. Let

\begin{align*} \vec r_i \amp = x_i\hat i + y_i\hat j + z_i\hat k \equiv (x_i,\ y_i,\ z_i),\\ \vec r_f \amp = x_f\hat i + y_f\hat j + z_f\hat k\equiv (x_f,\ y_f,\ z_f). \end{align*}

Then, the displacment vector \(\Delta \vec r\) has the following components form.

\begin{align*} \Delta \vec r \amp = \left( x_f-x_i,\ y_f-y_i,\ z_f- z_i \right), \end{align*}

Its convenient to write the changes in coordinates as \(\Delta x,\ \Delta y,\ \Delta z\text{.}\)

\begin{equation} \Delta \vec r = \left(\Delta x,\ \Delta y,\ \Delta z \right),\tag{4.11} \end{equation}

with

\begin{equation*} \Delta x = x_f-x_i,\ \ \Delta y = y_f-y_i,\ \ \Delta z = z_f- z_i. \end{equation*}

An example of the resolution of a displacement vector in the \(xy\)-plane is displayed in Figure 4.8.

\begin{align*} \amp \vec r_1 = 1\hat u_x + 3\hat u_y\ [\text{cm}]\\ \amp \vec r_2 = 4\hat u_x + 1\hat u_y \ [\text{cm}]\\ \amp \vec s_{12} = (4-1)\hat u_x + (1-3)\hat u_y.\ [\text{cm}] \end{align*}

Figure 4.8. Displacement vector in terms of the Cartesian unit vectors.

Note that regardless of the placement of the displacement vector, the projections of the beginning and ending of the displacement vector on the Cartesian axes give the length of vectors along the Cartesian axes that make up the original displacement vectors. You can say that \((x_2 -x_1) \hat u_x\) along the \(x\)-axis and \((y_2-y_1) \hat u_y\) along the \(y\)-axis add up to the displacement vector shown in the figure.

Subsection 4.2.1 Independence of Displacement Vectors from Coordinate System

We have already mentioned that the displacement vector does not require any reference point for its definition. We demonstrate here by analytic means that the displacement vector is independent of coordinate system as shown in Figure 4.9. If you pick another place for the origin, say the point \(O'\) [read O-prime], and use a different orientation for the coordinate axes than the one for the origin \(O\text{,}\) then you will get different numerical values for the coordinates for points \(P_1\) and \(P_2\text{.}\)

Let us denote the two coordinates systems by \(Oxyz\) and \(O'x'y'z'\) respectively. The coordinates for points \(P_1\) and \(P_2\) in the \(O'x'y'z'\) system will be \((x'_1,y'_1,z'_1)\) and \((x'_2,y'_2,z'_2)\) respectively, which will be different from the coordinates \((x_1,y_1,z_1)\) and \((x_2,y_2,z_2)\) for the same points in the \(Oxyz\) system. However, you will find that the difference in the coordinates in the two coordinate systems will be the same:

\begin{equation*} (x'_1 -x'_1,\ y'_2-y'_1,\ z'_2-z'_1) = (x_2 -x_1,\ y_2-y_1,\ z_2-z_1). \end{equation*}

Figure 4.9. The displacement vector \(\vec s_{12}\) from point \(P_1\) to point \(P_2\) from the perspectives of two different coordinate systems. The triangle of vectors in triangles \(\triangle OP_1P_2\) and \(\triangle O'P_1P_2\) show that, even though the pairs \{ \(\vec r_1\text{,}\) \(\vec r_2\) \} and \{ \(\vec r^{\prime}_1\) \(\vec r^{\prime}_2\) \} may be different, the displacement vector from \(P_1\) to \(P_2\) is the same in the two coordinate systems: \(\vec s_{12} = \vec r_2 - \vec r_1 = \vec r^{\prime}_2 - \vec r^{\prime}_1\text{.}\)

You can also see this directly in terms of the triangle of vectors in triangles \(\triangle OP_1P_2\) and \(\triangle O'P_1P_2\text{.}\) The vector addition shows that, even though the pairs \{ \(\vec r_1\text{,}\) \(\vec r_2\) \} and \{ \(\vec r_1^{\prime}\text{,}\) \(\vec r_2^{\prime}\) \} may be different, the displacement vector from \(P_1\) to \(P_2\) is the same in the two coordinate systems:

\begin{equation} \vec s_{12} = \vec r_2 - \vec r_1 = \vec r_2^{\prime} - \vec r_1^{\prime}.\tag{4.12} \end{equation}

Example 4.10. Displacement Vector for 1D Motion.

A box moves a distance of \(2\, \text{ m}\) towards East. A coordinate system is chosen which has the \(x \) axis pointed towards East. (a) What are the components of the displacement vector in the given coordinate system? (b) Write the displacement vector using unit vectors along the Cartesian axes.

Answer.

(a) \(\Delta x = 2 \text{ m}, \Delta y = 0, \Delta z = 0.\) (b) \(\Delta \vec r = 2\text{ m }\hat i.\)

Solution 1. a

Suppose, the initial point is at the origin, then since the \(x\) axis is in the direction of movement, the final coordinate would be \((2\, \text{ m}, 0, 0)\text{.}\) Therefore, the \(x\text{,}\) \(y\text{,}\) and \(z\) components of the displacement vector are \(2\text{ m}\text{,}\) \(0\text{,}\) and \(0\) respectively.

Solution 2. b

With \(\hat i \) the unit vector towards positive \(x\) axis, the displacement vector will be \(\Delta \vec r = 2\text{ m }\hat i\text{.}\)

Example 4.11. Calculating Displacement Vector in a Plane.

Your coordinates with respect to some Cartesian coordinate system is \((200 \text{ m}, 300\text{ m}) \text{.}\) After you have biked for \(5 \) minutes on a flat ground, your coordinates are \((-1000 \text{ m}, 1300\text{ m}) \text{.}\) What is your displacement during the \(5 \) minutes? Present your answer in (a) component form, and (b) magnitude-direction form with angle to be given with respect to \(x \) axis.

Answer.

(a) \(\left(-1200\text{ m}, 1000\text{ m} \right)\text{,}\) (b) \(1562\text{ m}\text{,}\) \(39.8^{\circ}\) clockwise from the negative \(x \) axis.

Solution 1. a

Note: I will leave units out from calculations, but put the units back at the end. We note that the motion is in the \(xy \) plane with \(z_i = 0 = z_f \text{.}\) With that we find the displacement vector’s components to be

\begin{equation*} \Delta \vec r = \left(-1000-200, 1300-300 \right) = \left(-1200\text{ m}, 1000\text{ m} \right). \end{equation*}

Solution 2. b

We convert component form to magnitude-angle forms by the same formulas that relate \((x,y) \) to \((r, \theta)\text{.}\)

\begin{align*} \amp \Delta r =\sqrt{1200^2 + 1000^2} = 1562\text{ m}.\\ \amp \theta = \tan^{-1}\left( \dfrac{1000}{-1200}\right) = - 39.8^{\circ} \end{align*}

Since the point \((-1200, 1000) \) is in the second quadrant. Therefore, the direction is \(39.8^{\circ}\) clockwise (since negative value) from the negative \(x \) axis.

Example 4.12. Direction of Displacement Vector in a Plane from Components.

You walk around in a room, and, after some time, the change in your coordinates with respect to a particular Cartesian coordinate system is given as \(( 3\, \text{ m}, 4\, \text{ m}, 0) \text{.}\) What is your displacement? Find both magnitude and direction.

Answer.

\(5\text{ m} \text{,}\) \(53^{\circ}\) counterclockwise from positive \(x\) axis.

Solution.

Note that the given information allows you to obtain the components of the displacement vector since we are already told that \(\Delta x = 3\, \text{ m}\) and \(\Delta y = 4\, \text{ m}\text{,}\) and \(\Delta z = 0\text{.}\) This gives the magnitude of the displacment to be

\begin{equation*} d = \sqrt{(\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2} = \sqrt{3^2 + 4^2} = 5. \end{equation*}

Putting the units back, we find the magnitude of displacement = \(5\text{ m} \text{.}\)

Since only \(x\) and \(y\) components of the displacment vector are non-zero, the vector is in the \(xy\)-plane. Therefore, we can specify the direction by the angle the vector makes with the \(x \) axis alone. This can be obtained by the arctangent formula.

\begin{equation*} \theta = \arctan{\left(\dfrac{4}{3}\right)} \approx 53^{\circ}. \end{equation*}

This says that the direction of the vector is in the \(xy\)-plane of the gives coordinate system at an angle counter-clockwise from the positive \(x\) axis.

Direction requires description. Note again that the angle itself is not the direction - if you choose to give the angle with respect to the positive \(y \) axis, the value will be \(-37^{\circ} \) for the same direction in the plane. So, the value of angle, in itself, is not the full information about the direction - you need to state what the angle means in the real space. Minus in \(-37^{\circ} \) refers to the clockwise direction as you look down from the positive \(z \) axis.

Example 4.13. Adding Displacement Vectors.

You travel from your home to the base of a mountain, and then, climb the mountain. The coordinates of your home, base of the mountain and the top of the mountain in a particular coordinate system are: home \((0,0,0) \text{,}\) base \((4000 \text{ m}, 3000 \text{ m}, 0)\text{,}\) peak \((4500 \text{ m}, 2500 \text{ m}, 800 \text{ m} )\text{.}\)

Find the magnitude and direction of the net displacement from your home to the peak (a) directly, and (b) by adding the two displacements, from home to the base and from base to the peak. (c) Draw a vector diagram to show the relationship between three displacements: from home to the base, from base to the peak, and from home to the peak.

Answer.

(a) and (b) \(5210\text{ m}\text{.}\)

Solution 1. a

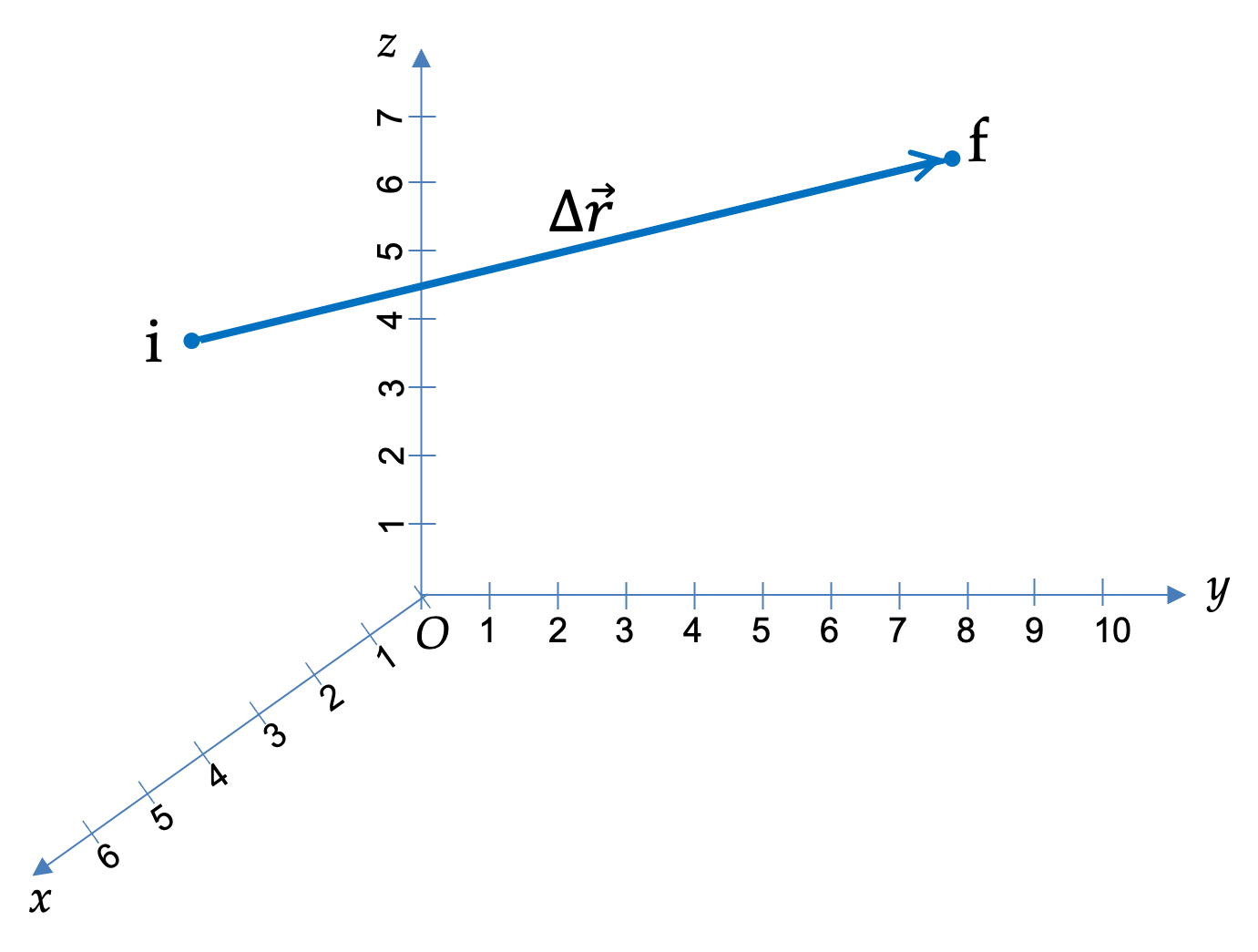
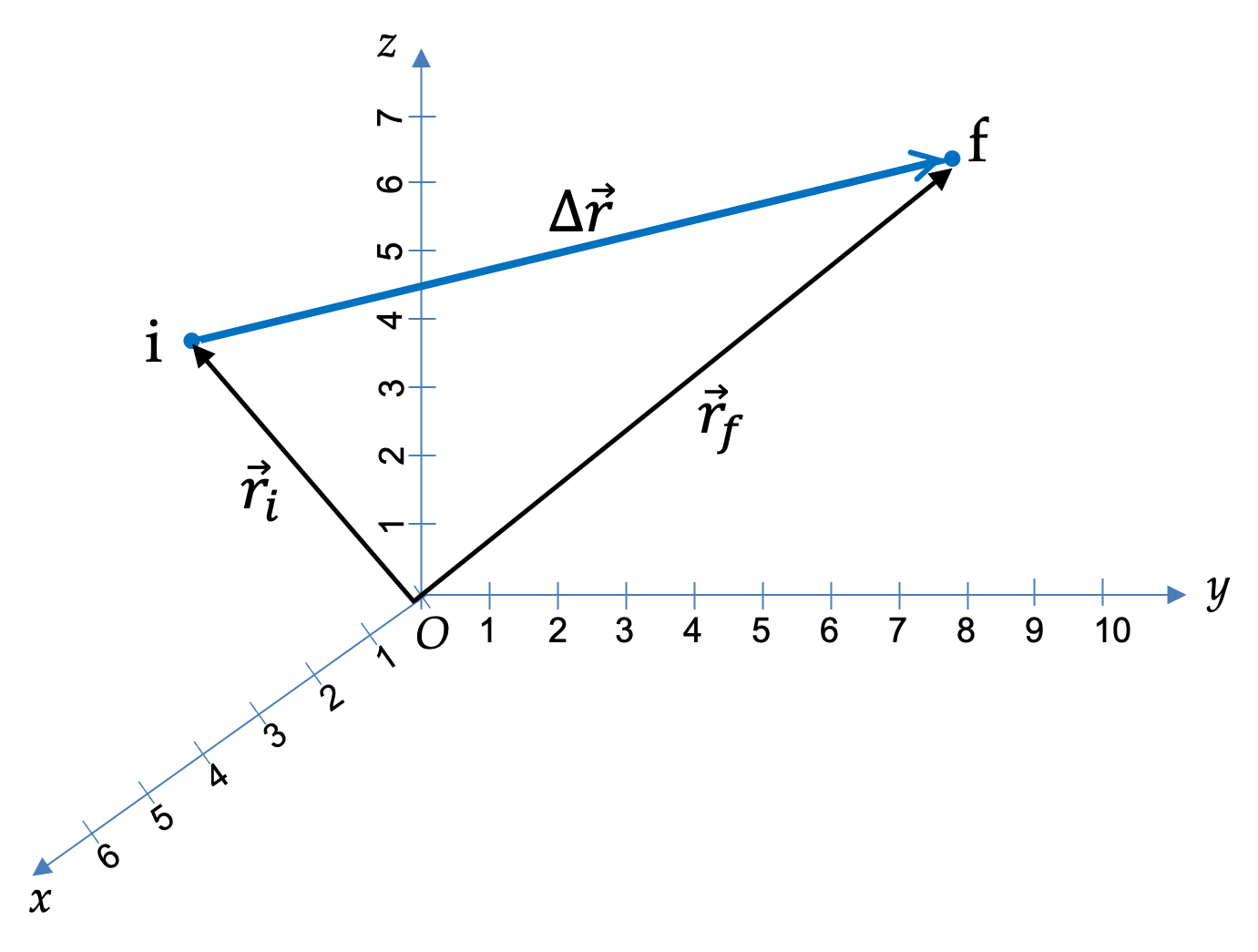
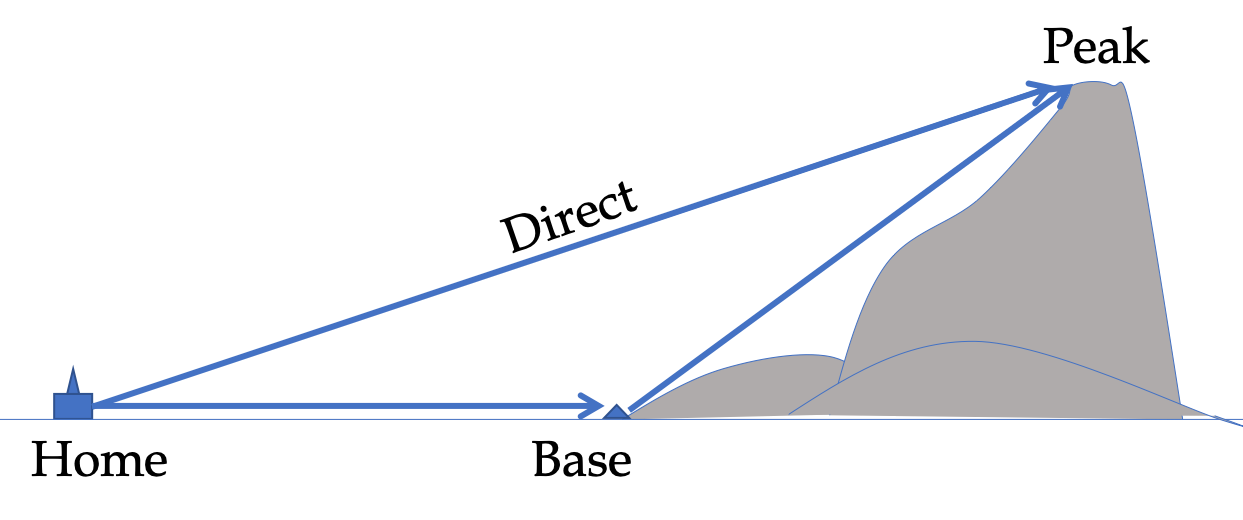
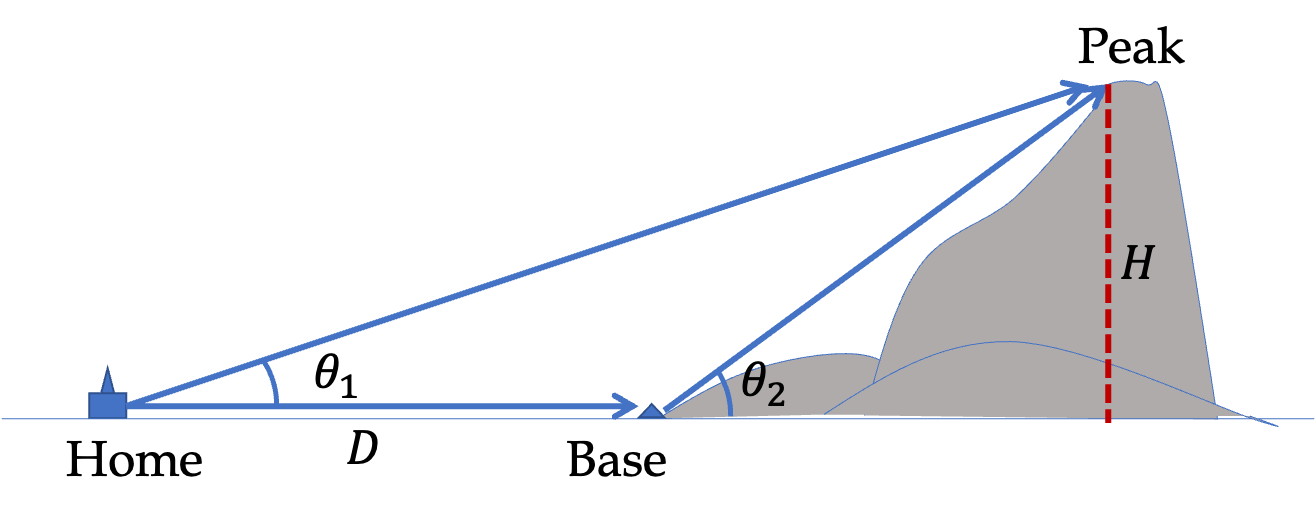
To find the displacement directly, we can use the coordinates of the home and the peak. We will suppress writing units in calculations and put the units back in at the end. The net displacement written in terms of the components along the Cartesian axes are

\begin{align*} \Delta \vec r_{\text{net}} \amp = (x_f-x_i, y_f-y_i, z_f-z_i) \\ \amp = [(4500-0), (2500-0), (800-0)] = (4500, 2500, 800). \end{align*}

Therefore, the components of the displacement vectors are

\begin{equation*} \Delta x = 4500\text{ m}, \Delta y = 2500\text{ m}, \Delta z = 800\text{ m}. \end{equation*}

Magnitude. From these components, we can determine the magnitude \(d_{\text{net}}\text{.}\)

\begin{align*} d \amp = \sqrt{(\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2}\\ \amp = \sqrt{4500^2 + 2500^2 + 800^2} \approx 5210 \end{align*}

Therefore, the magnitude of the net displacment from home to the peak is \(5210\text{ m} \text{.}\)

Direction for 3-dimensional vector. Unlike the two-dimensional situaiton, now we need to specify two angles. We will choose the spherical coordinate angles, which are the polar angle \(\theta \) with respect to the positive \(z \) axis, and azimuth angle \(\phi \) that the projection of the vector in the \(xy\)-plane makes with the \(x \) axis.

\begin{align*} \theta \amp = \arctan\left( \dfrac{(\Delta x)^2 + (\Delta y)^2}{\sqrt{(\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2}} \right) \\ \amp = \arctan\left( \dfrac{\sqrt{4500^2 + 2500^2}}{5210} \right) \approx 81^{\circ}\\ \phi \amp = \arctan\left( \dfrac{\Delta y}{\Delta x} \right) \\ \amp = \arctan{\left(\frac{2500}{4500}\right)} \approx 29^{\circ} \end{align*}

Since, the polar angle and azimuthal angles are in the first octant, we do not need to make any adjustments. The angles can be read off to say that the direction of the projection of the peak in the \(xy\) plane is \(\approx 29^{\circ} \) counterclockwise from the positive \(x \) axis and and \(\approx 81^{\circ} \) towards the \(xy\)-plane from the \(z \) axis.

Other ways of specifying direction. One can also find the direction of a vector by working out two of the angles, \(\theta_x \text{,}\) \(\theta_y \text{,}\) and \(\theta_z \text{,}\) the vector makes with the \(x \text{,}\) \(y \text{,}\) and \(z \) axes respectively by using the direction cosines.

\begin{align*} \amp \cos\, \theta_x = \dfrac{\Delta x}{ \sqrt{(\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2} }\\ \amp \cos\, \theta_y = \dfrac{\Delta y}{ \sqrt{(\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2} }\\ \amp \cos\, \theta_z = \dfrac{\Delta z}{ \sqrt{(\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2} } \end{align*}

Solution 2. b

Let us use subscripts 1, 2, and 3 to denote home, base, and peak. The two displacements from home to base and from base to the peak are

\begin{align*} \Delta \vec r_{12} \amp = [(4000-0), (3000-0), (0-0)] \\ \Delta \vec r_{23} \amp = [(4500-4000), (2500-3000), (800-0)] \end{align*}

The vector equation for the net displacement \(\Delta \vec r_{text{net}} \) is

\begin{align*} \Delta \vec r_{text{net}} \amp = \Delta\vec r_{12} + \Delta\vec r_{23} \\ \amp = [ 4000 + 500, 3000 -500, 0 + 800] \\ \amp = (4500, 2500, 800 ) \end{align*}

This is the same vector as found in part (a) by using direct method between home and the peak.

Solution 3. c

The figure for this part is in Figure 4.14

Figure 4.14. Figure for Example 4.13(c).

Exercises 4.2.2 Exercises

1. Finding the Final Position from Initial Position and Displacement.

A particle moves a distance of \(5.5\text{ mm} \) parallel to the \(y \) in the direction of positive \(y \) axis over a duration of \(1.5\, \mu\text{s}\) from a position of coordinates \((10.0\text{ mm}, 9.5\text{ mm}) \) in the \(xy\)-plane. At what position did the particle end up?

Hint.

\(\vec r_f = \vec r_i +\Delta\vec r\text{.}\)

Answer.

\(\vec r_f = (10.0\text{ mm}, 15.0\text{ mm}) \text{,}\) or, \(18.0\text{ mm}\) in \(56.3^{\circ}\) counterclockwise from the positive \(x \) axis.

Solution.

The problem statement gives us the initial position and the displacement, and we need to find the final position.

\begin{equation*} \Delta\vec r = \vec r_f - \vec r_i\Longrightarrow \vec r_f = \vec r_i +\Delta\vec r. \end{equation*}

We can add the two vectors on the right side by writing them in component form.

\begin{equation*} \vec r_i = (10.0\text{ mm}, 9.5\text{ mm}),\ \ \Delta\vec r = (0, 5.5\text{ mm}). \end{equation*}

Therefore,

\begin{equation*} \vec r_f = (10.0\text{ mm}, 15.0\text{ mm}) \end{equation*}

We can write this in the magnitude-direction as well.

\begin{align*} \amp r_f = \sqrt{10^2 + 15^2} = 18.0\text{ mm}.\\ \amp \theta = \tan^{-1}(15/10) = 56.3^{\circ}. \end{align*}

Since the point \((10.0\text{ mm}, 15.0\text{ mm}) \) is in the first quadrant, the angle is the counterclockwise direction from the positive \(x \) axis.

2. Finding the Initial Position from the Final Position and Displacement.

A boxer’s fist moved a distance of \(50 \text{ cm}\) parallel to the \(x \) axis but in the opposite direction to the direction of the positive \(x \) axis. The punch landed on the face of his opponent, where the coordinates is \((0, 30\text{ cm}, 168\text{ cm}) \text{.}\) Where was the boxer’s fist before he launched the punch?

Hint.

\(\vec r_i = \vec r_f -\Delta\vec r\text{.}\)

Answer.

\(\vec r_i = (50 \text{ cm}, 30\text{ cm}, 168\text{ cm})\text{.}\)

Solution.

The problem statement gives us the final position and the displacement, and we need to find the initial position.

\begin{equation*} \Delta\vec r = \vec r_f - \vec r_i\Longrightarrow \vec r_i = \vec r_f - \Delta\vec r. \end{equation*}

We can perform the subtraction on the right side by writing the vectors in component form.

\begin{equation*} \vec r_f = (0, 30\text{ cm}, 168\text{ cm}) ,\ \ \Delta\vec r = (-50 \text{ cm}, 0, 0). \end{equation*}

Therefore,

\begin{equation*} \vec r_i = (50 \text{ cm}, 30\text{ cm}, 168\text{ cm}). \end{equation*}

If we wish to write this as magnitude and direction, we would need two angles for the direction. I wouldn’t do that here.

3. Practice with a Friend: How high is the mountain?

The angles subtended by the direct sight to the mountain top from home and anothe location a distanc \(D\) closer to the mountain are \(\theta_1\) and \(\theta_2\text{,}\) respectively, as shown in Figure 4.15. Find the height of the mountain.

Answer check: Your answer will be in terms of \(D,\, \theta_1, \,\theta_2\text{.}\) For \(D=5.0\text{ km}\text{,}\) \(\theta_1=10^\circ\text{,}\) and \(\theta_2=15^\circ\text{,}\) \(H=2.6\text{ km}\text{.}\)

Prev Top Next