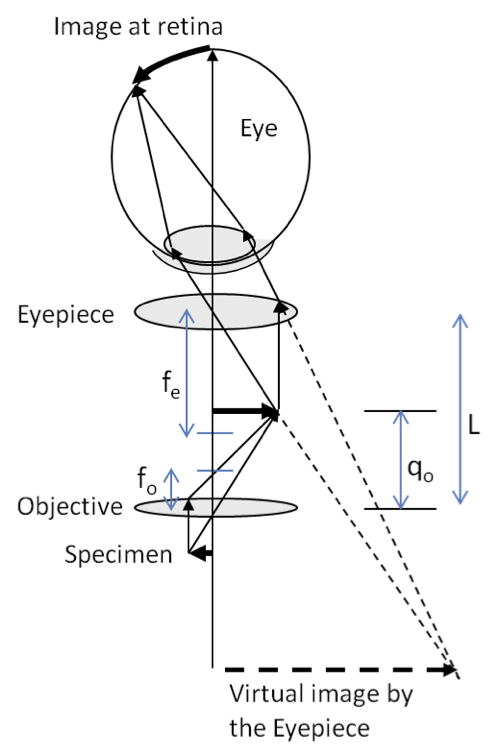
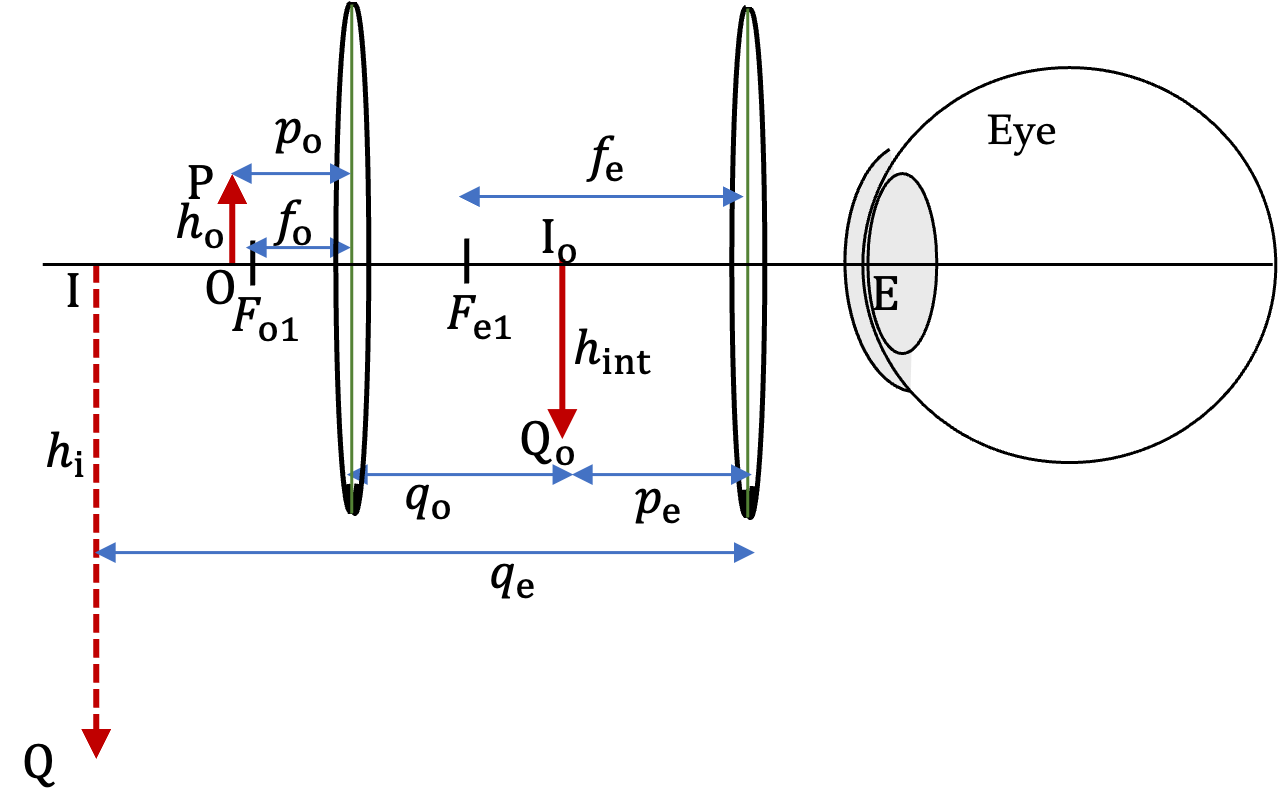
1. Perceived Size of a Microscopic Specimen in a Compound Microscope.
The objective and eyepiece of a compound microscope have focal lengths \(2.5\text{ cm}\) and \(10.0\text{ cm}\) respectively. You use this microscope to observe a \(70\, \mu\text{m}\) specimen placed \(3.0\text{ cm}\) from the objective. Assuming your near point is \(25\text{ cm}\) from your eye, how large is would be the image you would perceive?
Hint.
Work out the magnification first. Since \(p_\text{o}\ne f_\text{o}\text{,}\) its best to find magnification of the objective by using \(m=-q/p\text{.}\)
Answer.
\(1.23\text{ mm}\text{.}\)
Solution.
We need to find \(q_0\) to find the magnification. We do that from the lens equation applied to the objective.
\begin{align*}
q_\text{o} \amp = \frac{p_\text{o}\, f_\text{o}}{p_\text{o} - f_\text{o}} \\
\amp = \frac{3 \times 2.5}{3- 2.5} = 15\text{ cm}.
\end{align*}
This gives objective to be magnifying by a factor of
\begin{equation*}
m_\text{obj} = - q_\text{o}/p_\text{o} = -5.
\end{equation*}
That is the objective is \(5\times\text{.}\) The magnification of the eyepiece/eye is
\begin{equation*}
M_\text{eyepiece} = 1 + \frac{n_p}{f_\text{e}} = 1 + \frac{25\text{ cm}}{10\text{ cm}} = 3.5.
\end{equation*}
That is the eyepiece is \(3.5\times\text{.}\) Now, we multiply the two to get Therefore,
\begin{align*}
M_\text{microscope} \amp = -5\times 3.5 = -17.5.
\end{align*}
Therefore, the size perceived will be \(70\times 17.5\) \(= 1225\,\mu\text{m}\) \(= 1.23\text{ mm}\text{.}\)