Example 6.35. A Box on Floor Pushed Against a Wall.
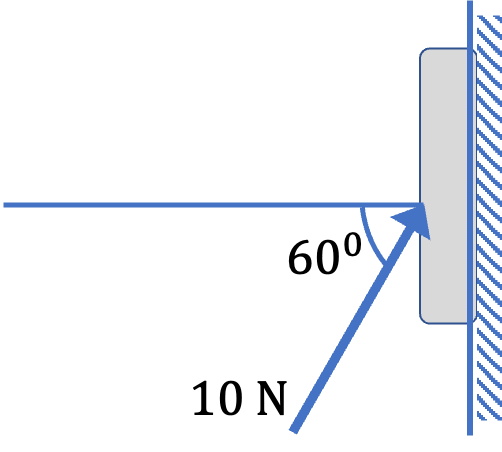
A 50-kg box is pushed against a wall by a force that acts horizontally and has magnitude \(200\text{ N}\text{.}\) Ignore any friction forces for this problem. What are the magnitudes and directions of all forces on the box?
Answer.
\(N_w = 200\text{ N},\ \ N_f=490.5\text{ N}. \)
Solution.
System: the 50-kg box.
Identifying forces on the system:
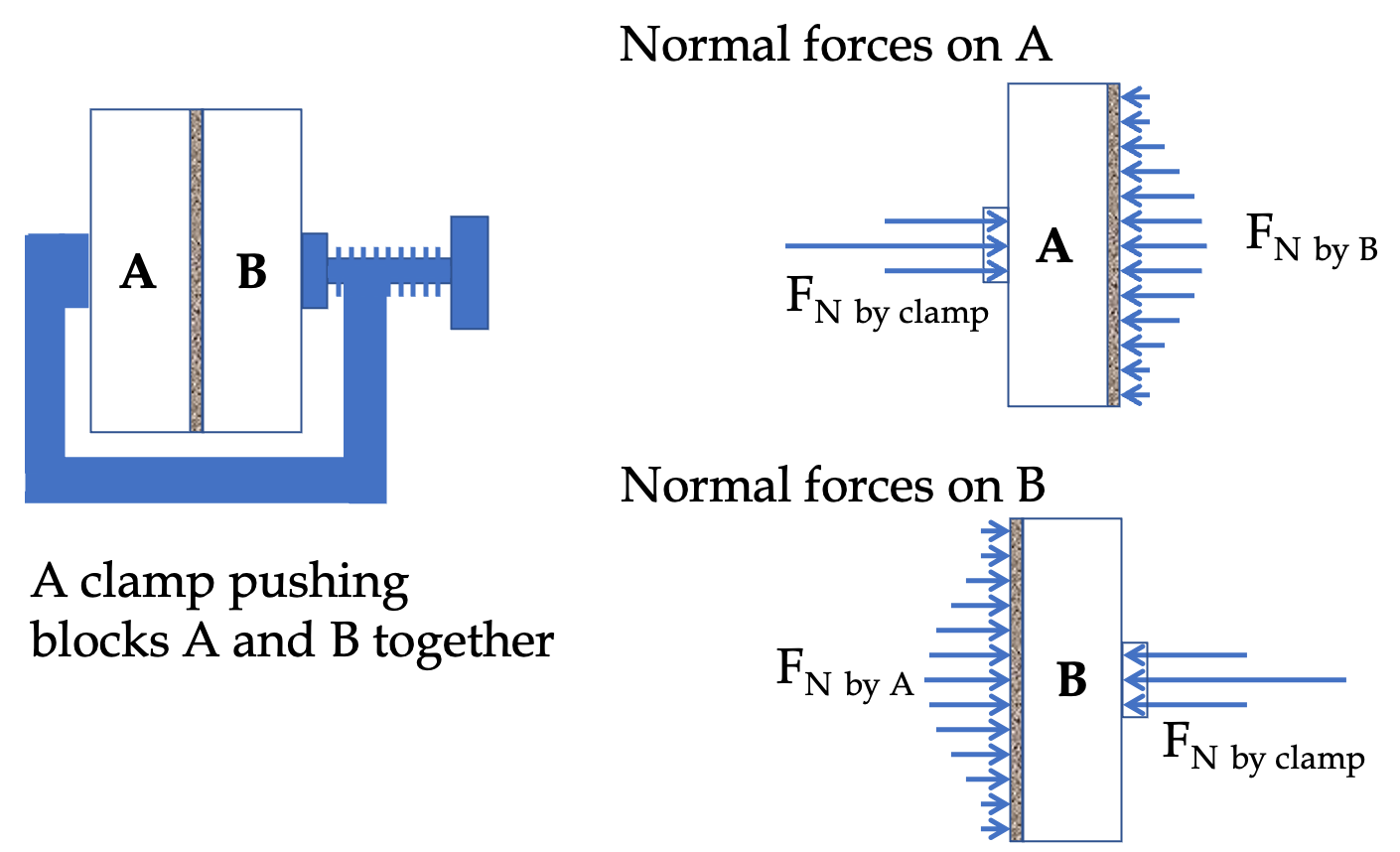
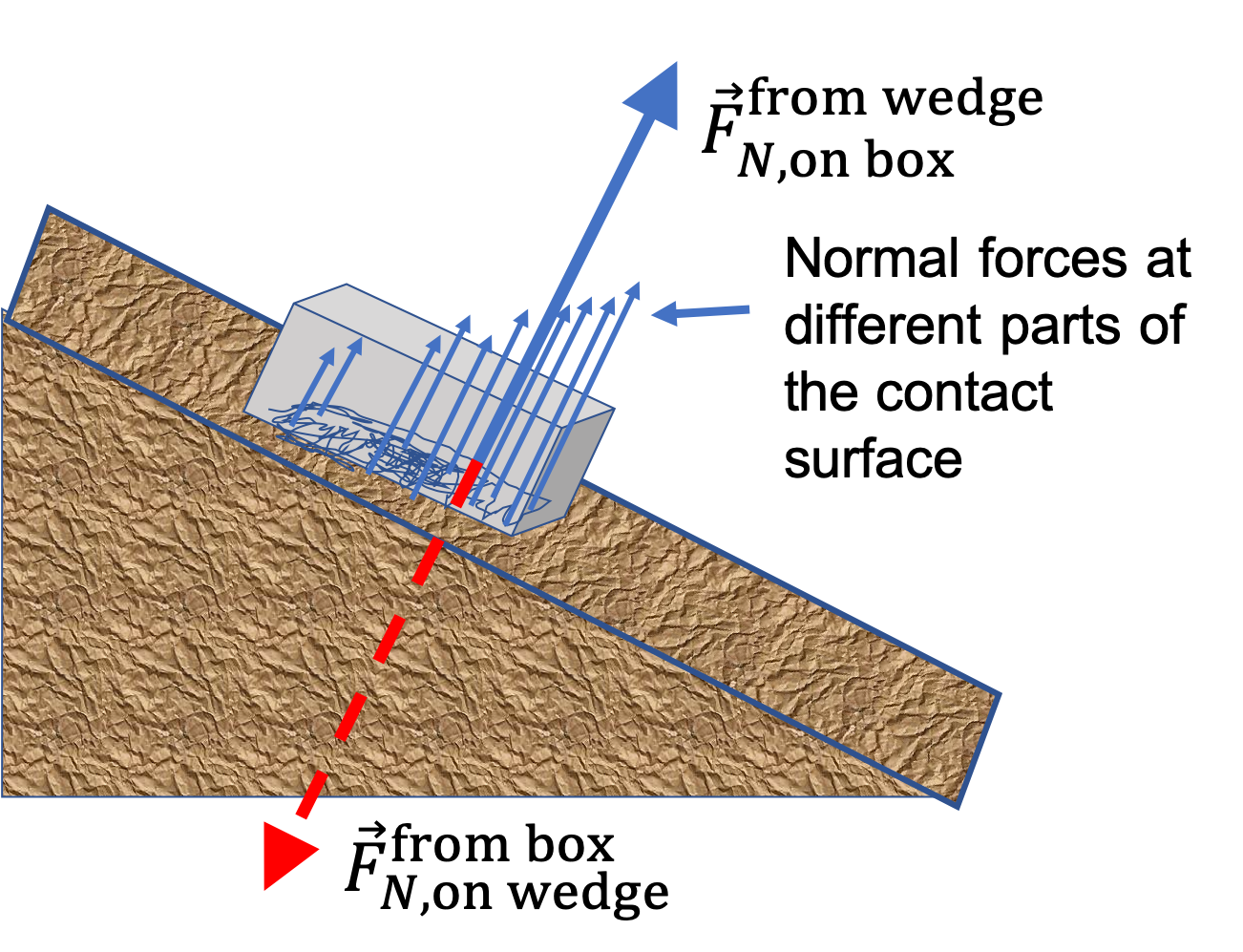
We first try to identify forces on the box. Usually a diagrram such as shown in Fig. (a) helps. Force on the box will come from other objects in the environment, either through a contact with them or through non-contact forces, such as gravity.
The objects in the environment are: Agent doing the pushing, Earth, Floor, and Wall. Each of them will apply force(s) on the box. Assuming no friction forces, we identify the following forces.
- Push, \(\vec F \text{,}\)
- Force of weight by Earth, \(\vec W\text{,}\)
- Normal Force from the floor, \(\vec F_N^{\text{from floor}}\text{,}\)
- Normal Force from the wall, \(\vec F_N^{\text{from wall}}\text{.}\)
If we were not given the instruction that friction force could be ignored, we would have two more forces.
- Static Friction Force from the floor, \(\vec F_s^{\text{from floor}} = 0\text{,}\)
- Static Friction Force from the floor, \(\vec F_s^{\text{from wall}} = 0\text{.}\)
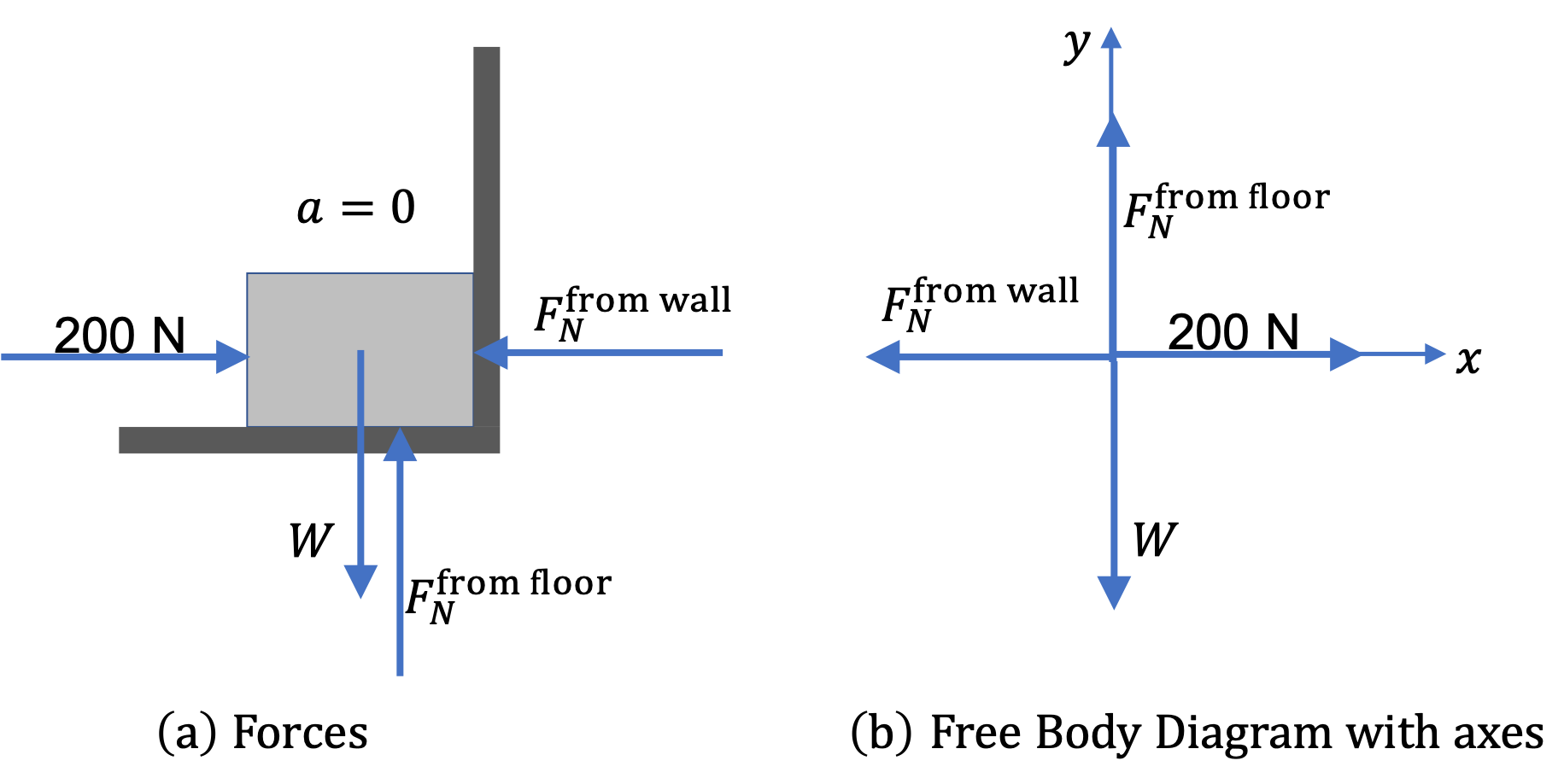
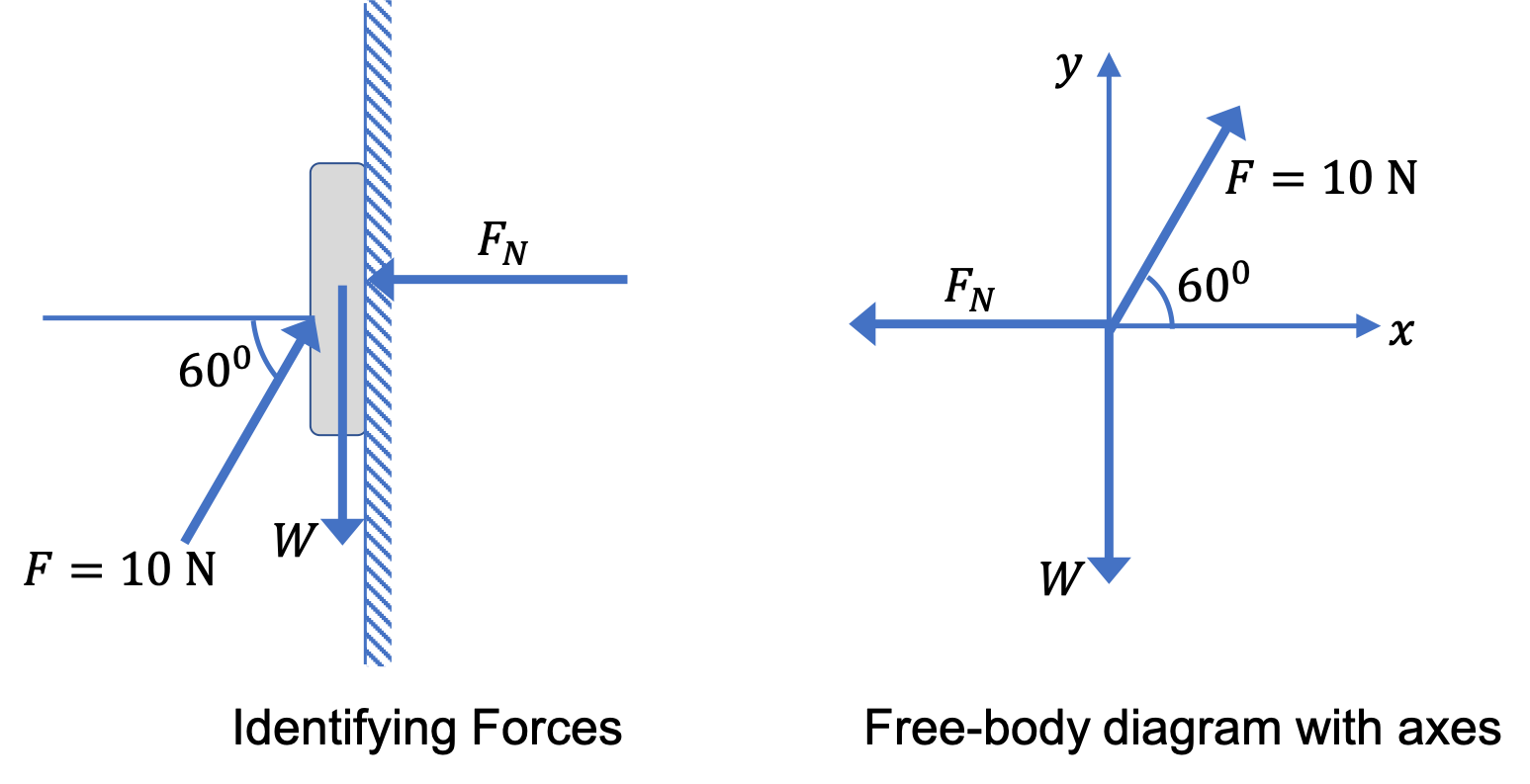
The Free-Body Diagram:
It is almost always very helpful to strip away the details and redraw a sketch of just the forces as in Figure 6.37(b). In this simplified picture, called the free-body diagram, we draw the force vectors with tails of all forces placed at the same point. We take the point where tails are located as the origin of a Cartesian coordinate system.
Choosing Cartesian Axes:
In this step, if we expect acceleration, then it is almost always helpful to point one of the Cartesian axes in the direction of the acceleration. But, if the acceleration is zero, or the direction of acceleration is unknown, then we prefer to draw axes that would simplify the computation of net force, which happens when most of the forces are along the axes.
Here, the acceleration is zero. Furthermore, we notice in Fig. Figure 6.37(a) that if we use axes horizontally and vertically, every force will be along the Cartesian axes. This will make computation of components of \(\vec F_{\text{net}}\) easier.
Generating equations of motion:
Since \(\vec a = 0 \text{,}\) our equation of motion is:
\begin{equation*}
\vec F_{\text{net}} = 0,
\end{equation*}
which would result in two equations, one along each Cartesian direction.
Although not necessary, sometimes it is helpful to collect the components in a table form. Let us use simpler symbols \(N_f \) and \(N_w \) for the magnitudes of the normal forces from the floor and from the wall respectively.
| Force | \(x\)-component | \(y\)-component |
| Weight | \(0\) | \(-490.5\text{ N}\) |
| Applied Force | \(200\text{ N}\) | \(0\) |
| Normal from the floor | 0 | \(N_f\) |
| Normal from the wall | -N_w | \(0\) |
The \(x \) component of the net force will be just the sum of the \(x \) components of all the forces. Similarly for the \(y \) component of the net force.
\begin{align*}
\amp F_{x}^{\text{net}} = 0 + 200 + 0 - N_w,\\
\amp F_{y}^{\text{net}} = -490.5 + 0 + N_f + 0.
\end{align*}
Since \(\vec F_{\text{net}} = 0\text{,}\) we get the following two equations.
\begin{align*}
\amp 0 + 200 + 0 - N_w = 0\\
\amp -490.5 + 0 + N_f + 0 = 0.
\end{align*}
Solve for the desired quantities:
This turns out to be easy here since each of the two equations of motion has only one unknown.
\begin{equation*}
N_w = 200\text{ N},\ \ N_f=490.5\text{ N}.
\end{equation*}
Interpret the result:
We have found the magnitudes of the two normal forces on the box. The normal force from the floor has magnitude \(490.5\text{ N}\) and pointed up, and the normal force from the wall has magnitude \(200\text{ N}\) and pointed away from the wall and perpendicular to the wall.