The practical importance of the resonance phenomenon is seen dramatically in the choice of the frequency of the driving power source in delivering power to the rest of the circuit. The energy at any instant is stored in the capacitor and the inductor, but only the resistor in the circuit dissipates energy. Therefore, the average energy used by the circuit during an interval will be equal to the product of the instantaneous power into the resistor and the interval of time. Thus, the energy deposited in the resistor in an interval of time between \(t\) to \(t+dt\) will be given by
\begin{equation*}
P(t) dt = I(t) V_R(t),
\end{equation*}
where \(I(t)\) is the current through the resistor and \(V_R\) is the voltage drop across the resistor. From Ohm’s law we can replace \(V_R\) by \(I R\) and obtain
\begin{equation*}
P(t) dt = I_0^2 R\cos^2(\omega t+\delta),
\end{equation*}
where \(\delta\) is the phase of the current relative to the phase of the driving EMF. The energy deposited in the resistor per cycle is obtained by integrating this expression over a period, \(T = 2\pi/\omega\text{.}\)
\begin{equation*}
\textrm{Energy(one cyle)}=\int_0^{T}P(t) dt = \frac{1}{2}I_0^2 RT.
\end{equation*}
Therefore, the average rate at which the energy is dissipated in the resistor will be \(\frac{1}{2}I_0R^2\text{.}\) This is the average power dissipated.
\begin{equation}
P_{\textrm{ave}} = \frac{\textrm{Energy(one cyle)}}{T} = \frac{1}{2}I_0^2R.\tag{40.45}
\end{equation}
Since the peak current
\(I_0\) is a function of the driving frequency
\(\omega\text{,}\) the average power delivered would also be a function of the frequency
\(\omega\) of the EMF source. Thus, the average power is maximum at the same frequency at which the peak current is maximum. We saw above that the peak current was maximum when the source EMF was oscillating at the same frequency as the natural frequency of the circuit.
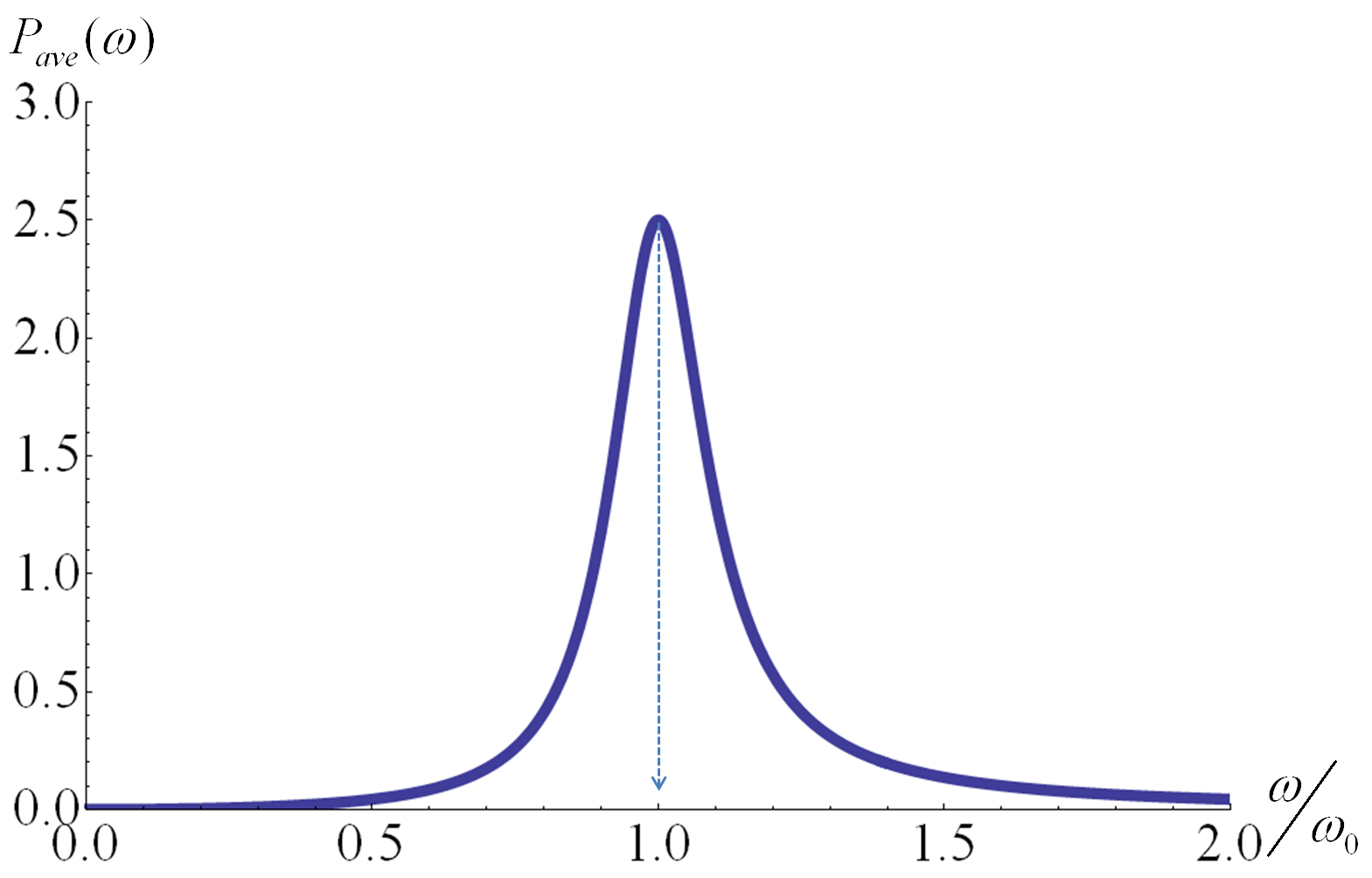
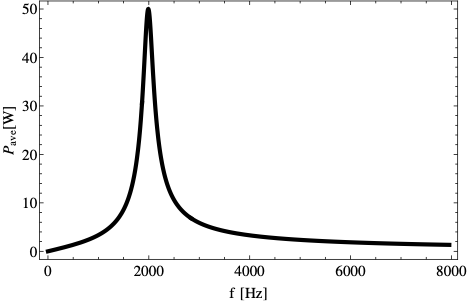
Figure 40.45 shows the resonance curve of average power.
The curve shows that the maximum power is delivered to the circuit when the circuit is driven at the natural frequency. Denoting the resonance frequency of power as \(\omega_R\) we have
\begin{equation*}
\omega_R = \omega_0 = \frac{1}{\sqrt{LC}}\ \ \ \textrm{(Resonance of Power.)}
\end{equation*}
This formula for the average power in the resistor differs from the power for the constant current circuit we had found in an earlier chapter. There, we had found that the power dissipated in a resistor is \(I^2R\text{,}\) but here we find that the average power is \(\frac{1}{2}I_0^2R\) where \(I_0\) is the amplitude of the oscillating current, which changes between \(-I_0\) and \(+I_0\) sinusoidally in time. It is possible to define an averaged current, called the {\bf root-mean squared current}, or the {\bf RMS-current}, \index{RMS current} we can rewrite the average power \(P_{\textrm{ave}}\) as a formula that is similar to a DC circuit.
\begin{equation*}
I_{\textrm{rms}} = \frac{I_0}{\sqrt{2}}
\end{equation*}
This will give the average power dissipated as
\begin{equation*}
P_{\textrm{ave}} = R\: I_{\textrm{rms}}^2.
\end{equation*}