Section 3.8 Chapter Summary
A vector has both direction and magnitude and adds to other vectors of the same kind by the parallelogram law of addition. The addition of vectors can be done graphically or analytically. In the graphical addition, one places vectors in a tip-to-tail fashion mindful of the direction of each vector in space. The vector from the tail of the first vector to the tip of the last vector is equal to the sum.
Analytically, vectors are decomposed into Cartesian components.
\begin{equation*}
\vec A = A_x \hat u_x + A_y \hat u_y + A_z \hat u_z \equiv A_x \hat i + A_y \hat j + A_z \hat k.
\end{equation*}
The components along each axis add separately from the components along other axes. Thus, the sum of the \(x\)-components of all vectors gives the \(x\)-component of the sum, and similarly for the \(y\) and \(z\)-components. For \(\vec C = \vec A + \vec B\text{,}\) we have
\begin{equation*}
C_x \hat i + C_y \hat j + C_z \hat k = (A_x + B_x)\, \hat i + (A_y + B_y)\, \hat j + (A_z + B_z)\, \hat k
\end{equation*}
Pythagoras theorem can be used to find the magnitude of a vector from its components and simple trigonometry is used to find the direction in space.
\begin{equation*}
A = \sqrt{A_x^2 + A_y^2 + A_x^2}.
\end{equation*}
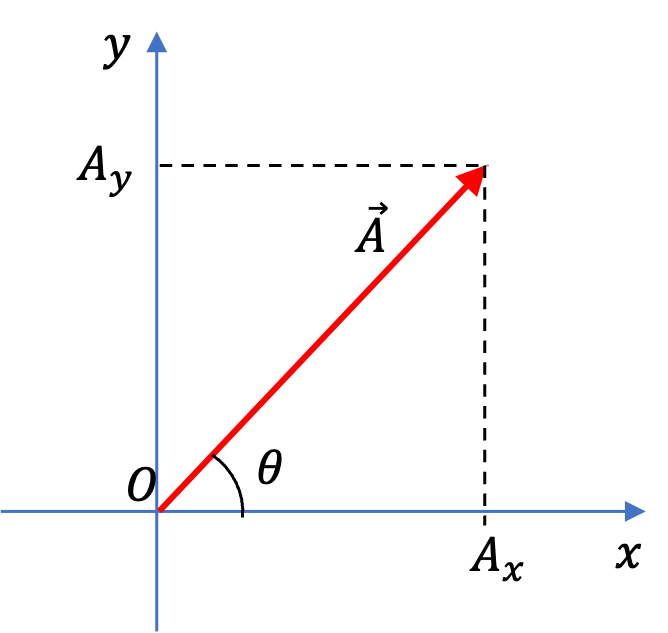
If a vector is in \(xy\) plane, we get a simpler case.
\begin{equation*}
\vec A = A_x \hat i + A_y \hat j.
\end{equation*}
Then, magnitude is simply \(A = \sqrt{A_x^2 + A_y^2}\text{.}\)
The direction in \(xy\)-plane is indicated by the angle the vector makes with respect to the \(x\)-axis.
\begin{equation*}
\theta = \tan^{-1}\left( \frac{A_y}{A_x} \right),
\end{equation*}
where the positive angle is counterclockwise with respect to the \(x\)-axis in first or third quadrant and if the angle is negative, it the clockwise angle into the second or the fourth quadrant.
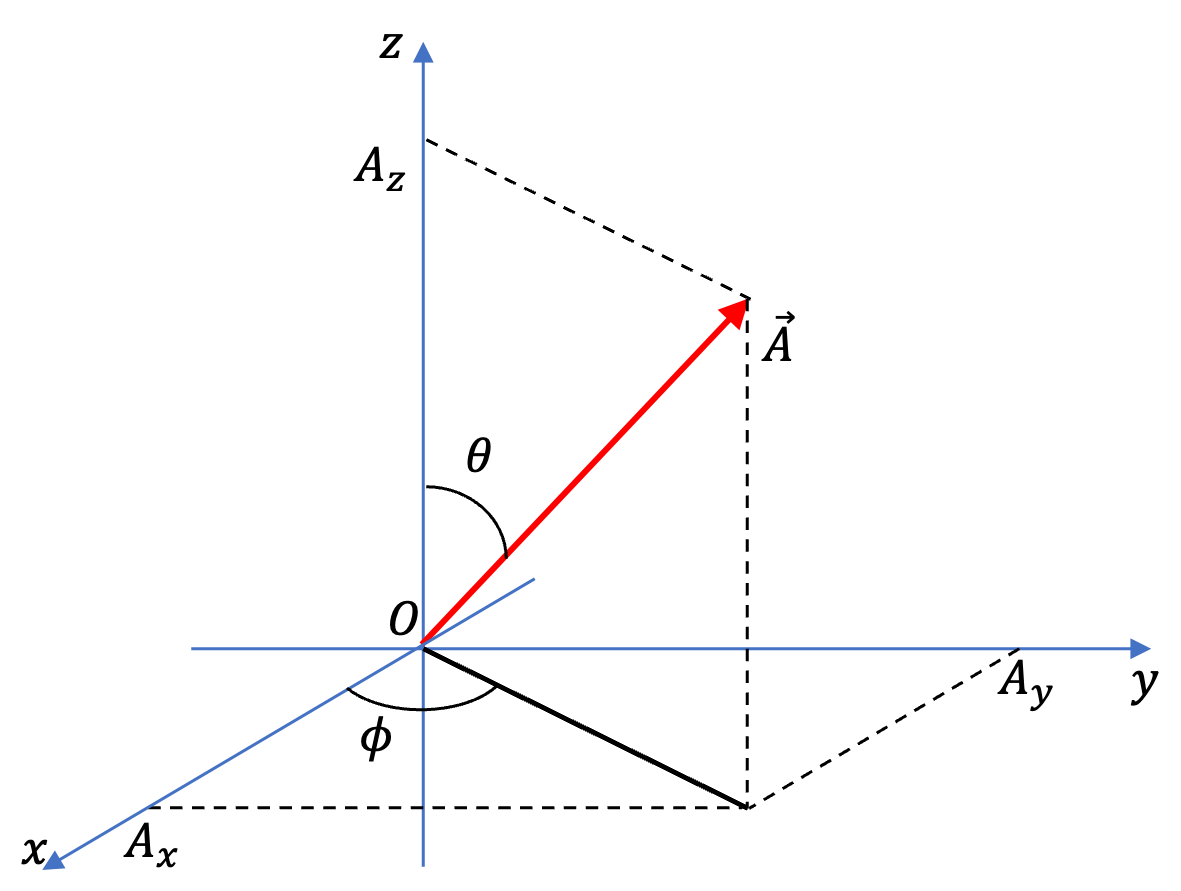
For a vector in three-dimensional space, we often use the spherical coordinate angles to indicate the directions. The polar angle \(\theta\) and the azimuthal angle \(\phi\) shown in Figure 3.98 are computed by
\begin{align*}
\amp \theta = \cos\left(\frac{A_z}{A} \right) \\
\amp \phi = \tan^{-1}\left( \frac{A_y}{A_x} \right)
\end{align*}
Vectors can be multiplied by ordinary real numbers. A positive number only scales the size of the vector, but a negative number also reverses the direction of the vector. We studied in detail the rules of two different types of multiplication of a vector with another vector. In the scalar multiplication, also called dot product, the result is a scalar number. The resulting number is equal to the product of the magnitudes of the two vectors and the cosine of the angle between them. The scalar product written in analytic form is equal to the sum of products of the Cartesian components of the vectors.
\begin{equation*}
\vec A\cdot \vec B = A B \cos\theta = A_xB_x + A_yB_y + A_zB_z.
\end{equation*}
The vector product, also called the cross product, gives rise to another product whose magnitude is equal to the the product of the magnitudes of the two vectors and the sine of the angle between them, and the direction is in the direction to the normal to the plane of the two vectors. The direction of the cross product vector is obtained by a right-hand rule. The cross product written in analytic form gives the components of the product in terms of the components of the vectors multiplied.
\begin{align*}
\amp (\vec A \times \vec B)_x = A_y B_z - A_z B_y,\\
\amp (\vec A \times \vec B)_y = A_z B_x - A_x B_z,\\
\amp (\vec A \times \vec B)_z = A_x B_y - A_y B_x,
\end{align*}

