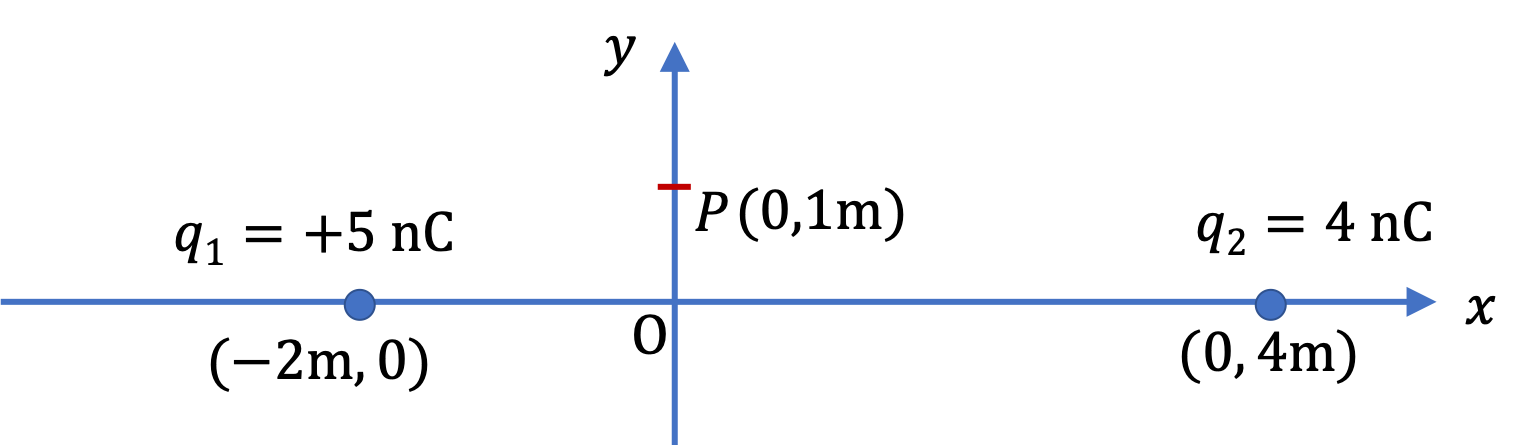
Example 29.30. Electric Field of Two Charges at a Point on Line Joining the Charges.
Find the electric field at the origin.
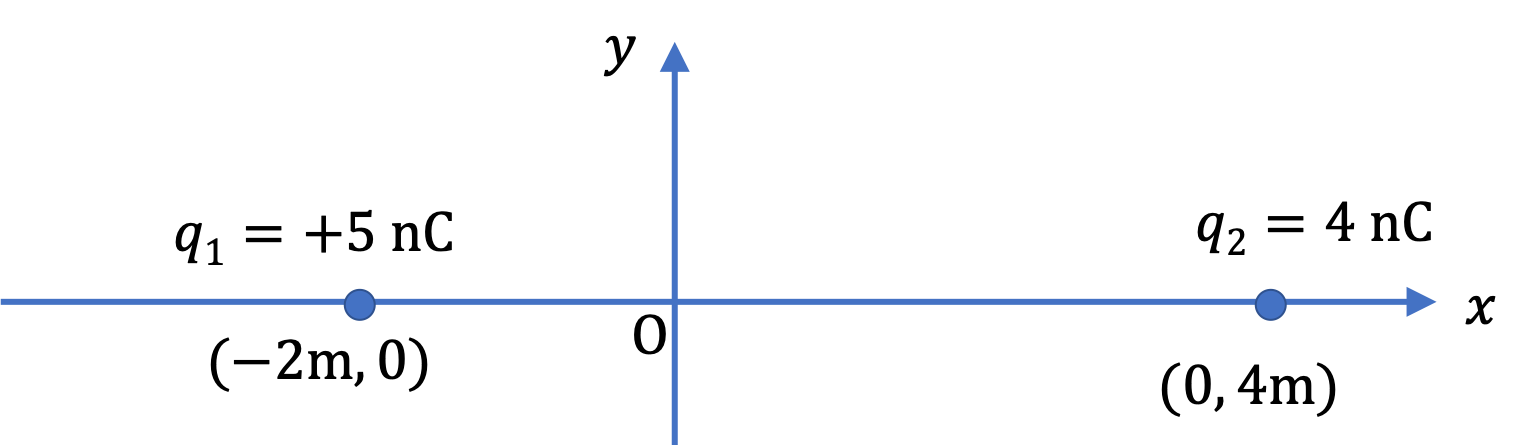
Answer.
\(9\text{ N/C}\) in the positive \(x\) direction.
Solution.
The following figure shows the electric field of the two charges at the origin are along the \(x\) axis, but they are in the opposite direction. We will compute \(x\) components of the two fields so that we can deal with their addition through the sign of the components.
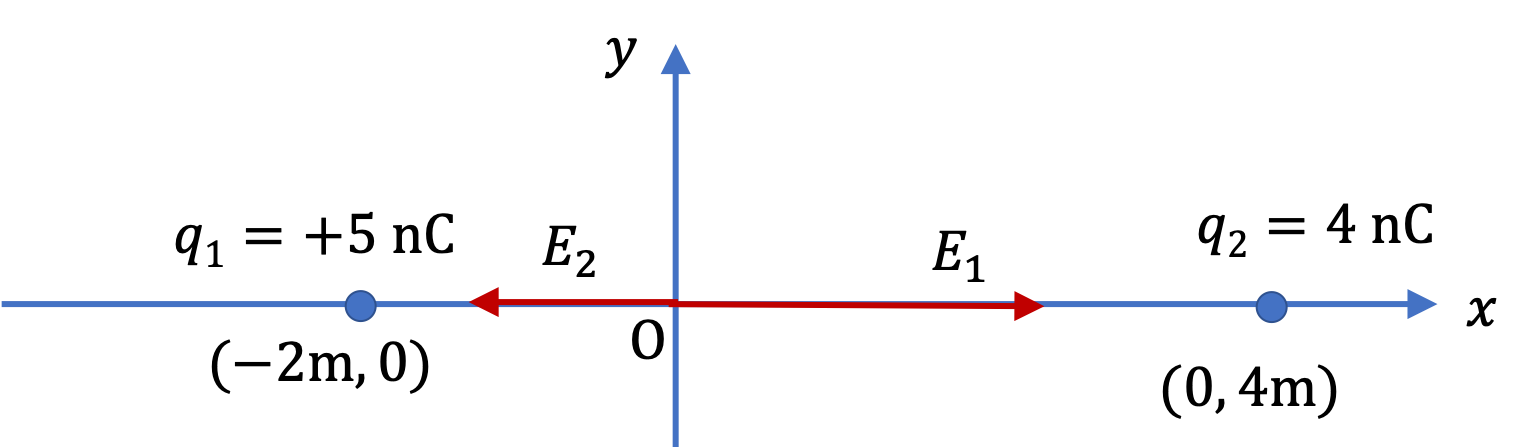
The \(x\) component of the fields are
\begin{align*}
E_{1x} \amp = + k\dfrac{|q_1|}{r_1^2} = 9\times 10^{9} \times \dfrac{5\times 10^9}{2^2} = 11.25\text{ N/C}, \\
E_{2x} \amp = - k\dfrac{|q_2|}{r_2^2} = -9\times 10^{9} \times \dfrac{4\times 10^9}{4^2} = -2.25\text{ N/C}.
\end{align*}
Therefore, \(x\) component of the net electric field at origin is
\begin{equation*}
E_x = E_{1x} + E_{2x} = 11.25 + (- 2.25) = 9\text{ N/C}.
\end{equation*}
This is the only non-zero component of the field. Therefore, electric field at origin has magnitude \(9\text{ N/C}\) and direction in the positive \(x\) direction.