Unit Vectors and Components

Section 3.2 Unit Vectors and Components

Unit vectors are special types of vectors that have magnitude 1, no units, and are pointed in a specified direction in space. In this section, we will learn to find unit vectors in the direction of another given vector. We will also learn to use unit vectors that point in the direction of Cartesian axes to decompose any vector in terms of its Cartesian components. We will also learn how to build a vector from its Cartesian components.

Subsection 3.2.1 Definition

Given any vector \(\vec A\text{,}\) we can obtain a vector, called unit vector in the direction of \(\vec A\) that has the same direction as \(\vec A\) but has unit magnitude by simply dividing \(\vec A\) by its length \(A\text{.}\) We will often denote the unit vector corresponding to a vector by placing a carat symbol \(\wedge \) over the symbol of the vector in place of arrow. We may also use alternative symbol built with \(\wedge \) over letter \(u\) wubscripted by the symbol of the vector.

\begin{equation} \hat u_A \equiv \hat{A} = \frac{\vec A}{|\vec A|}.\tag{3.8} \end{equation}

It’s important to note that unit vector has the same direction as the original vector from which it is formed since dividing by a positive number does not change the direction. Another thing to note is that since we divide by the same unit as the unit of \(\vec A\text{,}\) the unit vector DOES NOT HAVE ANY UNTIS.

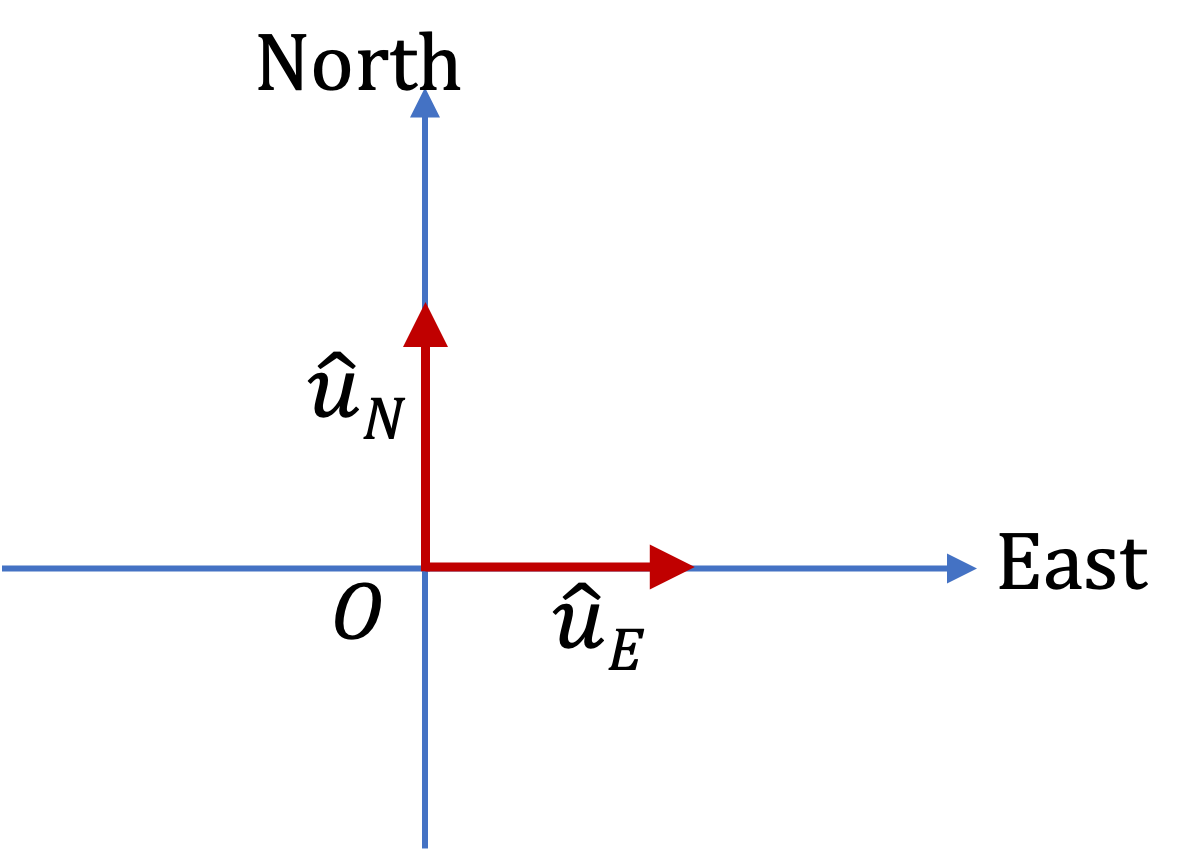
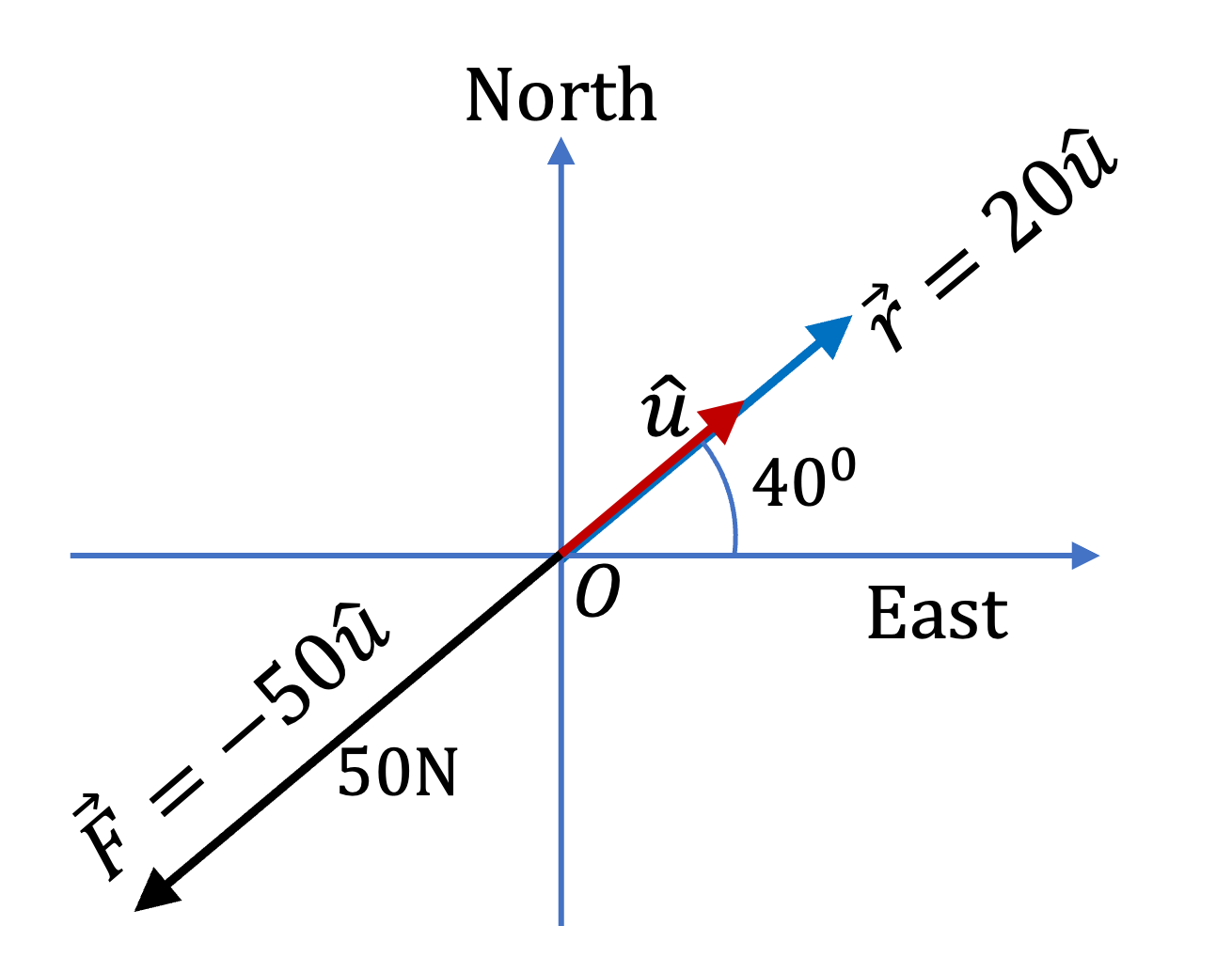
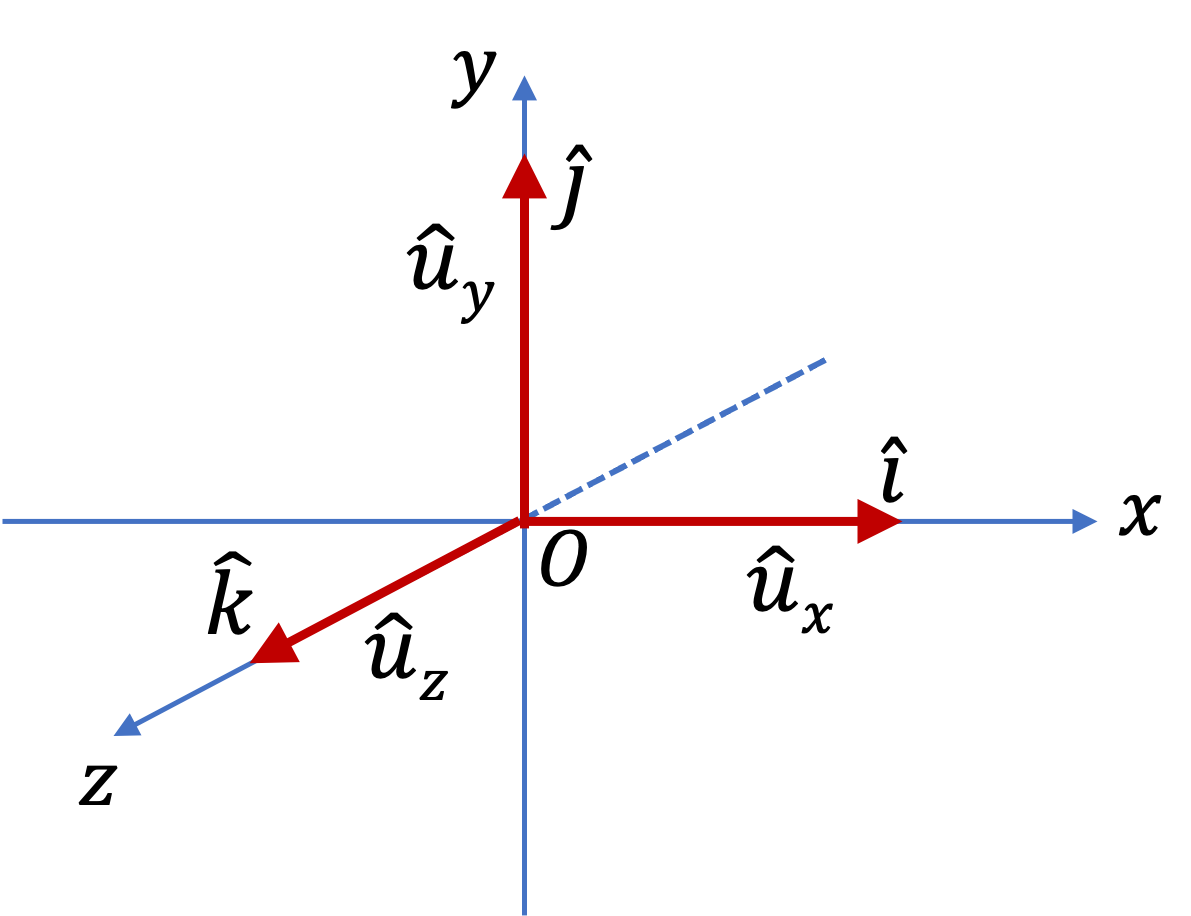
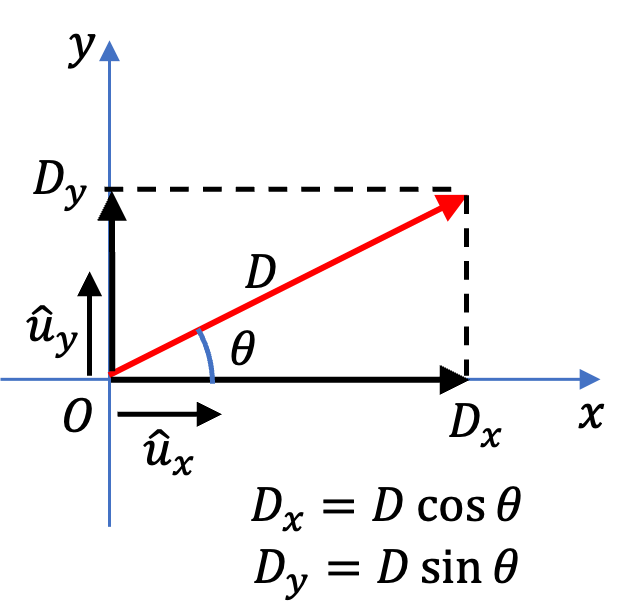
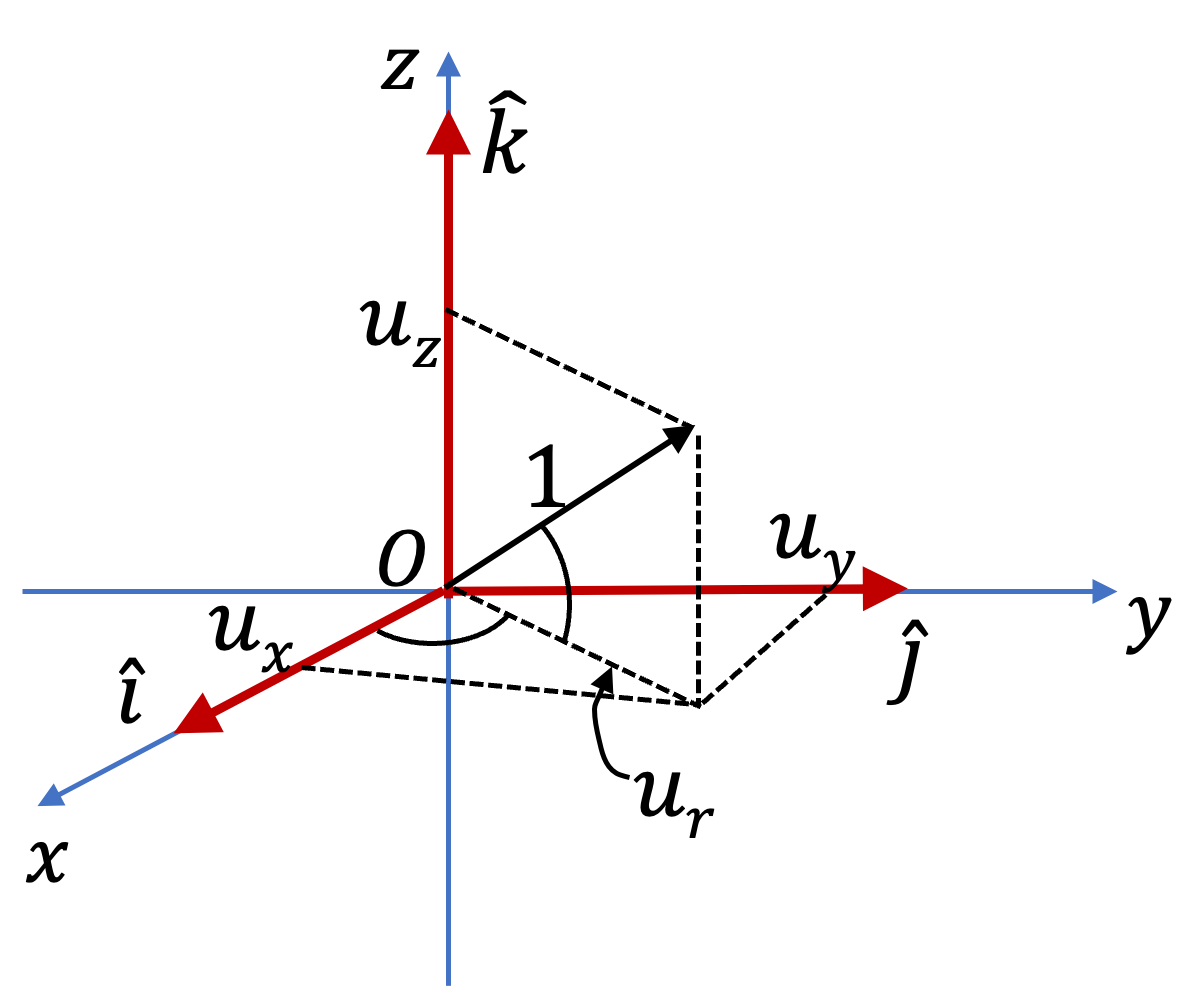
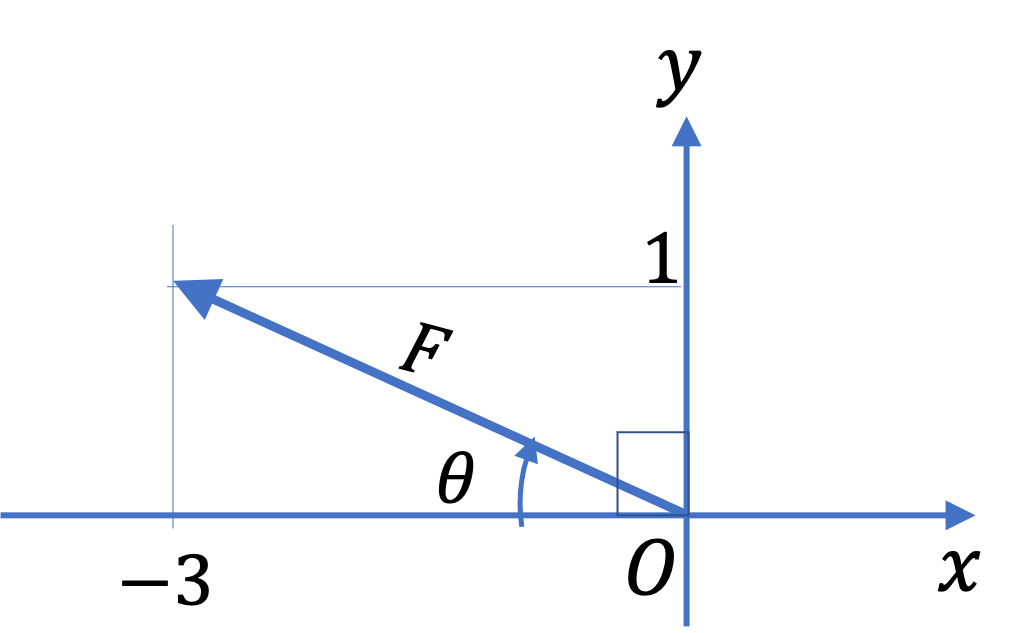
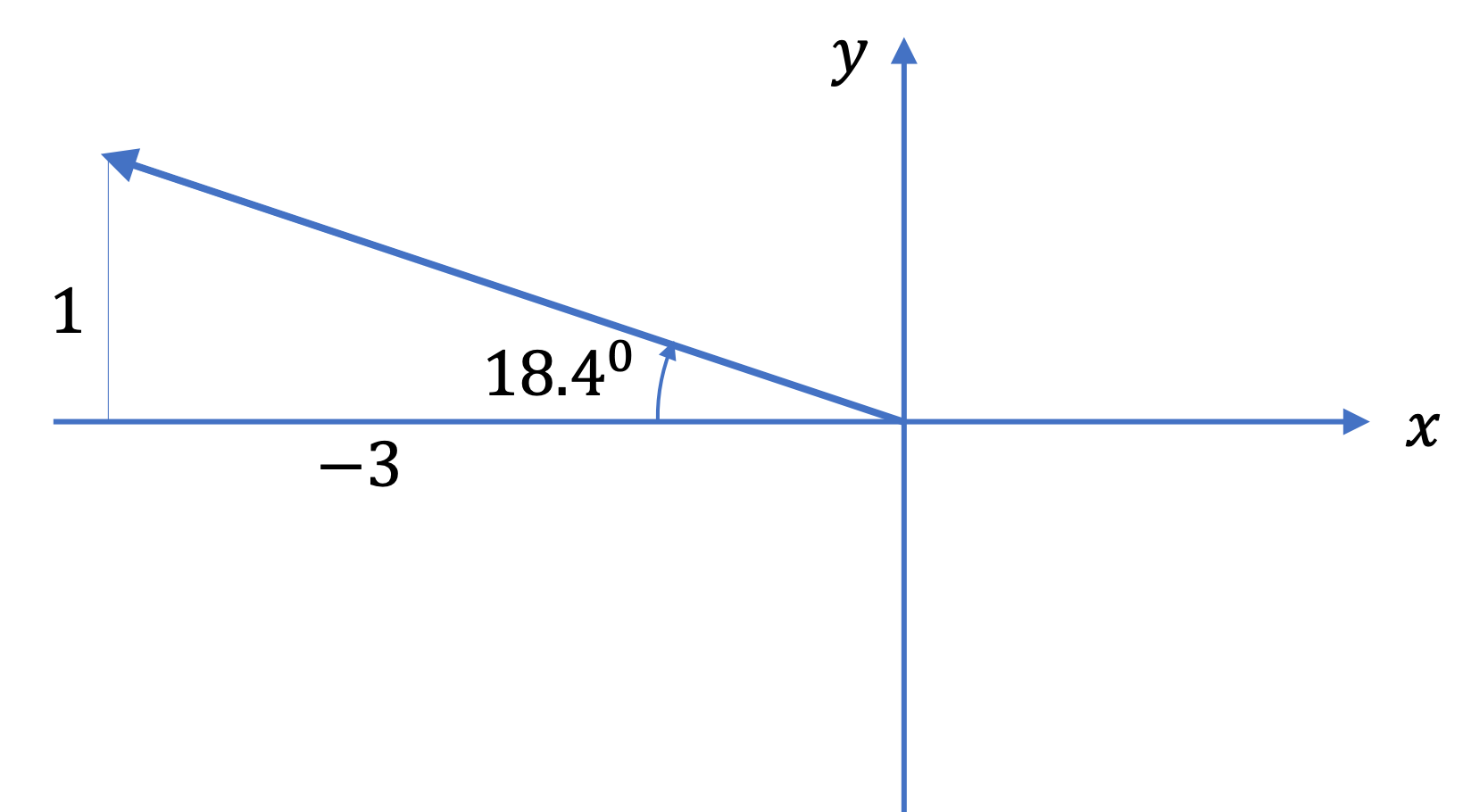
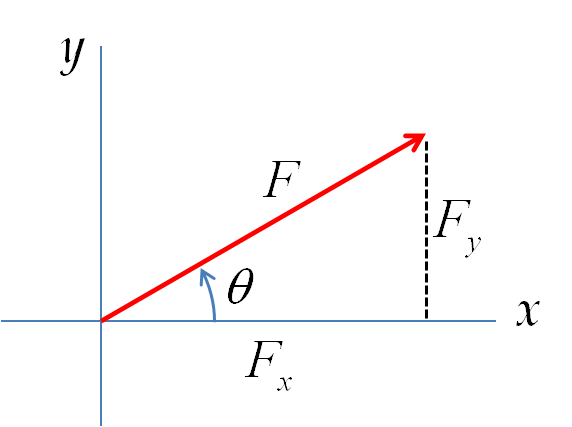
Example 3.30. Find Unit Vector in the Direction of a Given Vector.

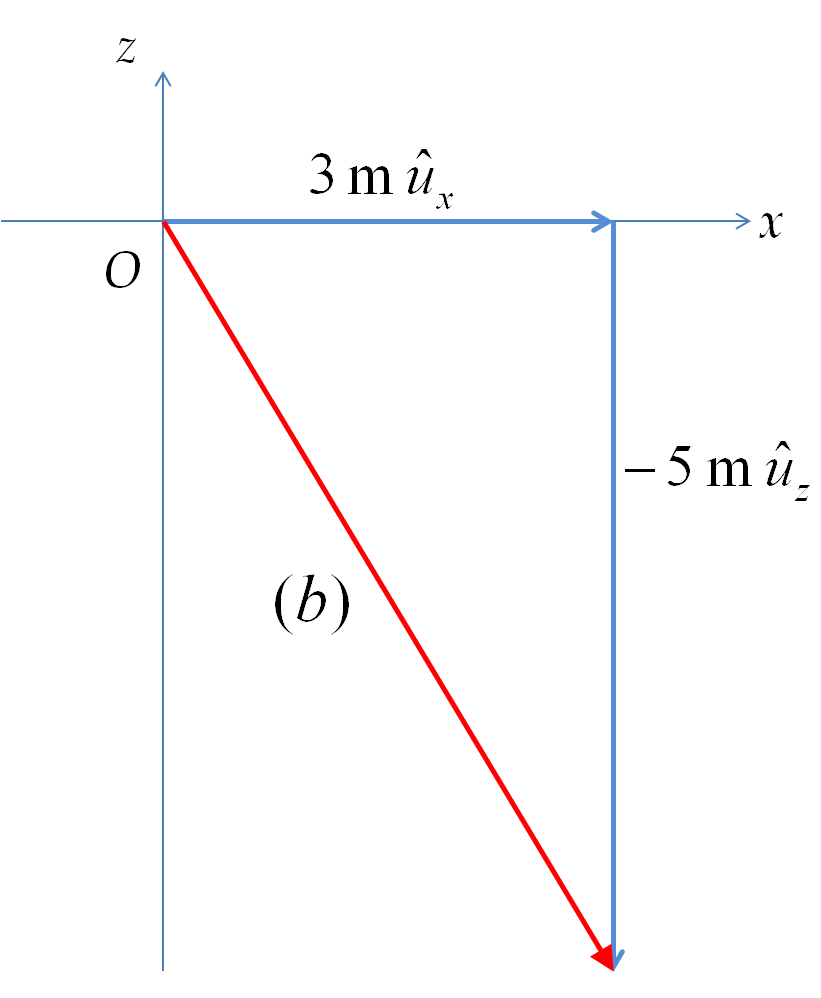
Find unit vectors in the directions of the following vectors. (a) \((10\ \textrm{N})\ \hat u_x + (-5\ \textrm{N})\ \hat u_y\text{,}\)

Solution.

The magnitude of the given vector = \(\sqrt{(10\ \textrm{N})^2 + (-5\ \textrm{N})^2} = 11.2\ \textrm{N}\text{.}\) Therefore, a unit vector \(\hat u\) in the direction of this vector is

\begin{equation*} \hat u = \frac{(10\ \textrm{N})\ \hat u_x + (-5\ \textrm{N})\ \hat u_y}{11.2\ \textrm{N}} = 0.89 \ \hat u_x + (- 0.45)\ \hat u_y. \end{equation*}

Since I have rounded off the answer, the magnitude of this unit vector may not be exactly 1. Let us check the magnitude of this unit vector.

\begin{equation*} |\hat u | = \sqrt{0.89^2 + (- 0.45)^2} = 0.997, \end{equation*}

which is approximately 1 if we round to two digits. Note that the unit vector does not have any units.

Subsection 3.2.2 Using Multiples of Unit Vectors

Let’s first get a unit vector pointed in the North direction and learn to use it to build arbitrary vectors that point either in North or South directions.

Say, you have a position vector \(\vec r \) with magnitude, \(r=10 \) cm, pointed in the direction North. To get unit vector in the direction North, which we can denote by \(\hat u_N\) we will just divide \(\vec r \) by the magnitude \(r=10 \) cm.

\begin{equation*} \hat u_N = \dfrac{ (10\text{ cm}, \text{ North}) } { 10 \text{ cm} } = (1, \text{ North}). \end{equation*}

Figure 3.31. Unit vectors towards East and towards North.

Since multiplying a vector by a number just scales the vector, multiplying a unit vector by a number will give a vector that is as many times bigger or smaller. For example, \(\frac{1}{2} \hat u_N \) will be a vector that has length \(\frac{1}{2} \) and the direction same as the direction of \(\hat u_N\text{.}\) The \(2 \hat u_N \) will be a vector that has length \(2 \) and the direction same as the direction of \(\hat u_N\text{.}\) A \(-\hat u_N \) will be a vector that has length \(1 \) but the direction opposite to the direction of \(\hat u_N\text{.}\)

Thus, you can write any vector along North or South direction as a product of its magnitude and the \(\hat u_N \) vector. Say, you want a velocity vector \(\vec v\) of magnitude \(20 \) m/s pointed North, you can write it analytically as

\begin{equation*} \vec v = (20 \text{ m/s} )\, \hat u_N, \end{equation*}

and if you want a velocity vector of magnitude \(20 \) m/s pointed South, you would do the following

\begin{equation*} \vec v = -(20 \text{ m/s} )\, \hat u_N, \end{equation*}

where the negative sign will just flip the direction of the unit vector, i.e., \((-\hat u_N)\) is a vector with magnitude 1 and pointed towards South.

There is nothing special about the direction North, and our discussion above using the example of \(\hat u_N \) can be generalized to a unit vector in any arbitrary direction, such as East/West vectors, or any other vectors.

Example 3.33. Using Unit Vectors to Write Vectors Analytically.

Say, you have a unit vector \(\hat u \) in some direction, e.g., \(40^{\circ}\) North of East. Then, any vector in the \(40^{\circ}\) North of East direction or in exactly opposite direction can be written in as a number (with appropriate units and sign) times \(\hat u \text{.}\)

For instance, if we have a displacement vector \(\vec r\) of \(20 \text{ m}\) in the direction of the \(\hat u \) vector, then \(\vec r = 20\text{ m } \hat u\text{.}\) If you have a force vector \(\vec F\) of \(50 \text{ N}\) in the opposite direction, then \(\vec F = -50\text{ N } \hat u\text{.}\)

You can see that a unit vector provides a universal way of writing vectors which incorporates the direction information analytically rather than having to specify the direction in words and diagrams.

Subsection 3.2.3 Cartesian Unit Vectors

See Section 3.7 for a more complete treatment of Cartesian unit vectors. Here we will introduce basic definitions. The unit vectors towards positive \(x\text{,}\) positive \(y\text{,}\) and positive \(z\) axes are very helpful in working with vectors. We will see here that due to the parallelogram law of addition of vectors, any arbitrary vector can be written as a sum of three vectors, each along the three Cartesian axes.

The figure on the right shows a right-handed Cartesian system of axes with the three unit vectors pointed towards the corresponding positive axis directions. We will often denote these unit vectors by \(\hat u_x \text{,}\) \(\hat u_y \text{,}\) and \(\hat u_z \) respectively. At other times, we will denote them by their traditional symbols \(\hat i \text{,}\) \(\hat j \text{,}\) and \(\hat k \) respectively.

Now, let us see how any arbitrary vector can be written using these unit vectors. First let us consider a displacement vector \(\vec D_1\) of length \(10\text{ cm}\) pointed towards positive \(x\)-axis. This will be simply:

\begin{equation*} \vec D_1 = (10\text{ cm})\,\hat u_x. \end{equation*}

What if we had a displacement vector \(\vec D_2\) of length \(10\text{ cm}\) pointed towards NEGATIVE \(x\)-axis? We just need to use \(-\hat u_x\) in place of \(\hat u_x\text{.}\)

\begin{equation*} \vec D_2 = (10\text{ cm})\,(-\hat u_x), \end{equation*}

which we can also write as

\begin{equation*} \vec D_2 = -(10\text{ cm})\,\hat u_x. \end{equation*}

Example 3.36. Vector in \(xy\)-Plane.

Let us now consider a vector \(\vec D\) of length \(10\text{ cm}\) pointed at an angle \(30^\circ\) counterclockwise from the positive \(x\)-axis towards the \(y\)-axis. This vector is said to lie in the \(xy\)-plan. From the trigonometry of the right-angled triangle, it is easy to see that

\begin{align*} \amp X = 10\, \cos 30^\circ = 5\text{ cm}.\\ \amp Y = 10\, \sin 30^\circ = 5\sqrt{3}\text{ cm}. \end{align*}

Analytically, we write \(\vec D = 5\text{ cm} \hat i + 5\sqrt{3}\text{ cm} \hat j\text{.}\)

Now, we form Cartesian vectors \(\vec D_x \equiv \overrightarrow{OD_x} = D_x\, \hat u_x\) and \(\vec D_y \equiv \overrightarrow{OD_y} = D_y\, \hat u_y\text{.}\) We notice that \(\vec D_x\) and \(\vec D_y\) form the sides of a parallelogram (here rectangle) and the full vector is along the diagonal as shown in Figure 3.37. That means the full vector is just the sum of the two vectors along the axes.

\begin{equation*} \vec D = \vec D_x + \vec D_y = D_x\, \hat u_x + D_y\, \hat u_y. \end{equation*}

The numerical values multiplying the unit vectors are called Cartesian components of the vector. Thus, the number \(D_x\) is called the \(x\)-component of vector \(\vec D\text{,}\) which is itself not a number but a vector. And, \(D_y\) is called the \(y\)-component of vector \(\vec D\)

In general, an arbitrary vector \(\vec A \) with coordinate components \(A_x, A_y, A_z\) is often written as a sum of vectors along the Cartesian axes.

\begin{equation*} \vec A = A_x \hat u_x + A_y \hat u_y + A_z \hat u_z. \end{equation*}

Example 3.38. Position vector in xy-plane.

Here we will use \(\hat i\) and \(\hat j\) for unit vectors \(\hat u_x\) and \(\hat u_y\) respectively. For instance, say, we want a position vector \(\vec r = ( x=2 \text{ m}, y=-5 \text{ m}) \) in the \(xy\)-plane. Then, you can see that this vector will be a sum of two vectors: \(\vec r_1 = 2 \text{ m } \hat i \) and \(\vec r_2 = -5 \text{ m } \hat j \text{.}\) We write this as

\begin{equation*} \vec r = 2 \text{ m } \hat i - 5 \text{ m } \hat j. \end{equation*}

Example 3.40. Example of a Force Vector.

For example, if we have a force \(\vec F \text{,}\) say of magnitude \(50\text{ N} \) in the \(30^{\circ} \) North of East direction, then we will draw an arrow of appropriate size.

If we use a scale of \(1\text{ cm representing } 5\text{ N} \text{,}\) then we will draw a \(10\text{ cm}\)-long arrow, starting at origin and pointing in the direction of \(30^{\circ} \) counteclockwise to the positive \(x \) axis where I assume \(x \) axis is pointed towards East and \(y \) axis is towards North.

This will give the following component form of this force vector \(F_x = 50\text{ N }\cos\, 30^{\circ} = 43.3 \text{ N}\) and \(F_y = 50\text{ N }\sin\, 30^{\circ} = 20\text{ N}\text{.}\)

Example 3.42. Draw Vectors Written in Component Form.

Draw the following vectors written in component form. Here m is the unit meter.

\((2\ \text{m})\ \hat u_x + (4\ \text{m})\ \hat u_y\text{.}\)
\((3\ \text{m})\ \hat u_x + (-5\ \text{m})\ \hat u_z\text{.}\)
\((-1\ \text{m})\ \hat u_y + (4\ \text{m})\ \hat u_z\text{.}\)

Solution.

(a)

(b)

(c)

Example 3.46. Find Components of a Vector in Two Frames.

(a) Find the components of the vector given in Figure 3.47 with respect to the axes \(Oxyz\) and \(Ox'y'z'\text{.}\) The \(z\) and \(z'\)-axes are perpendicular to the given figure. Assume the given vector is entirely in the \(xy\)-plane of the two coordinate systems.

(b) Write the vector using the unit vectors along axes in the two different coordinates - you should have two answers, one for each coordinate system.

(c) Since there are two different representations for the same vector in the two different coordinates, and since the choice of coordinate system is arbitrary, what physical content do the values of components have for the vector?

Solution 1. a

Using the angle \(\theta = 30^{\circ}\) with respect to \(Ox\) direction, we can determine the \(x\)- and \(y\)-components, \((F_x,F_y)\) of the given vector \(\vec F\text{.}\)

\begin{align*} \amp F_x = (20\ \text{N})\ \cos(30^{\circ}) = 17 \ \text{N}\\ \amp F_y = (20\ \text{N})\ \sin(30^{\circ}) = 10 \ \text{N} \end{align*}

Similarly, using the angle \(\theta' = 40^{\circ}\) with respect to \(Ox'\) direction, we can determine the \(x\)- and \(y\)-components, \((F_x',F_y')\) of the given vector \(\vec F\text{.}\)

\begin{align*} \amp F_x' = (20\ \text{N})\ \cos(40^{\circ}) =15 \ \text{N}\\ \amp F_y' = (20\ \text{N})\ \sin(40^{\circ}) = 13 \ \text{N} \end{align*}

Solution 2. b

Let us use the same notation for the unit vectors that point towards the positive axes. The vector \(\vec F\) can be written as

\begin{equation*} \vec F = (17 \ \text{N})\ \hat u_x + (10 \ \text{N})\ \hat u_y\ \ \text{or}\ \ \vec F = (15 \ \text{N})\ \hat u_x^{\prime} + (13 \ \text{N})\ \hat u_y^{\prime} \end{equation*}

Solution 3. c

This exercise shows you that the physical information is in the magnitude and the direction of the vector, which do not depend upon your choice of coordinates. The values of the components do depend upon the choice of the coordinate directions. From the components we can construct the physical information contained in them.

Subsection 3.2.4 Direction Cosines

We have mentioned before that the direction of a vector in a three-dimensional space is often given by drawing the vector with its tail at the origin and then using the spherical coordinates \(\theta\) and \(\phi\text{,}\) the so-called polar and azimuthal angles. In the case of Earth, we use related latitude and longitude angles.

There is another way to state the direction. Again, we draw the vector with its tail at the origin and then we find the angle the vector makes with each of the Cartesian coordinate axes. The cosines of these angles are called direction cosines. Of course, these angles can be used to tell the direction of the vector as well.

In Figure 3.48, the direction cosines of vector \(\vec A\) are \(\cos\theta_x\text{,}\) \(\cos\theta_y\text{,}\) and \(\cos\theta_z\text{.}\) These angles, \(\theta_x\text{,}\) \(\theta_y\text{,}\) and \(\theta_z\text{,}\) are frequently referred to as \(\alpha\text{,}\) \(\beta\text{,}\) and \(\gamma\text{,}\) respectively.

After we discuss dot product of vector I will show that direction cosines are not all independent. Rather, they are related by the following identity.

\begin{equation} \cos^2\theta_x + \cos^2\theta_y + \cos^2\theta_z = 1.\tag{3.9} \end{equation}

Figure 3.48. Angles for direction cosines.

Checkpoint 3.49. Derive.

Derive Eq. (3.9).

Example 3.50. Angle Vectors Make with the Cartesian Axes.

Find the angles the following vector makes with positive \(x\text{,}\) \(y\) and \(z\)-axes: \(3\hat u_x +2 \hat u_y + 4\hat u_z\text{.}\)

Solution.

The angle of a vector with respect to the \(x\)-axis is obtained from the result \(\vec A\cdot \vec B = A B \cos\theta\) by picking one of the vectors as \(\hat u_x\text{.}\) similarly for other angles with the axes. We ill denote angles with \(x\)-, \(y\)-, and \(z\)-axes by letters \(\alpha\text{,}\) \(\beta\text{,}\) \(\gamma\text{,}\) respectively.

\(\cos\alpha = \frac{3}{\sqrt{3^2+2^2+4^2}} = 0.557\text{,}\) which gives \(\alpha = 56^{\circ}\text{.}\)

Similarly, \(\cos\beta = \frac{2}{\sqrt{3^2+2^2+4^2}} = 0.371\text{,}\) which gives \(\beta = 68^{\circ}\text{,}\) and \(\cos\gamma = \frac{4}{\sqrt{3^2+2^2+4^2}} = 0.742\text{,}\) which gives \(\gamma = 42^{\circ}\text{.}\)

Example 3.51. Unit Vector in an an Arbitrary Direction.

Suppose you are told that the velocity of a projectile is \(25\text{ m/s}\) in the direction of \(30^{\circ}\) above the direction of East. Let positive \(x \) axis be towards the East and the positive \(y \) axis be pointed up.

(a) Find \(x\) and \(y\) components of a unit vector in the stated direction.

(b) Write the given velocity vector in terms of the unit vector you found.

Answer.

(a) \(\hat u = \dfrac{\sqrt{3}}{2}\, \hat i + \dfrac{1}{2}\, \hat j\text{,}\) \(25\text{ m/s}\, \hat u\text{.}\)

Solution 1. a

We want a vector \(\hat u \) of unit magnitude in the direction described. We need to just find its \(x\) and \(y \) components.

\begin{align*} \amp u_x = 1\times \cos\, 30^{\circ} = \dfrac{\sqrt{3}}{2}\\ \amp u_x = 1\times \sin\, 30^{\circ} = \dfrac{1}{2}. \end{align*}

Therefore,

\begin{equation*} \hat u = \dfrac{\sqrt{3}}{2}\, \hat i + \dfrac{1}{2}\, \hat j. \end{equation*}

Solution 2. b

When we multiple a unit vector by a positive number we get a vector of the new length and the same direction, so, all we have to do to get the velocity in that direcion is just multiply the unit vector by the magnitude of the velocity.

\begin{equation*} \vec v = 25\text{ m/s}\, \hat u. \end{equation*}

Of course, this is same as

\begin{equation*} \vec v = 25\text{ m/s}\, \left( \dfrac{\sqrt{3}}{2}\, \hat i + \dfrac{1}{2}\, \hat j\right) \end{equation*}

Example 3.53. Unit Vector in the Direction of a Vector.

Suppose you want a unit vector in the same direction as the velocity vector given to you as \(\vec v = (3.0 \text{ m/s})\hat i + (4.0 \text{ m/s})\hat j\text{.}\) Find this unit vector.

Answer.

\(0.6\hat i + 0.8\hat j\)

Solution.

To get a unit vector, we just divide out the magnitude, which is

\begin{equation*} v = \sqrt{3^2 + 4^2} = 5 \end{equation*}

Now, we divide the original vector \(\vec v \) by its magnitude to get unit vector in the direciton of \(\vec v \text{.}\)

\begin{equation*} \hat u = \dfrac{ 3\hat i + 4 \hat j}{5} = 0.6\hat i + 0.8\hat j. \end{equation*}

Example 3.54. Unit Vector in Three Dimensions.

Suppose you want a unit vector in the direction of a star that is \(30^\circ\) above horizon above \(40^\circ\) North of East direction. Find a unit vector in the direction in terms of unit vectors along East, North, and Up.

Answer.

\(\hat u = 0.66 \hat i + 0.56 \hat j + 0.5 \hat k.\)

Solution.

Let us use \(\hat i\) towards East, \(\hat j\) towards North, and \(\hat k\) towards Up. First we project a unit vector in the plane containing Up and “\(40^\circ\) N of E” directions. We will call them as \(u_z\) and \(u_r\text{,}\) respectively. We get

\begin{align*} \amp u_z = 1\, \sin(30^\circ) = \frac{1}{2}.\\ \amp u_r = 1\, \cos(30^\circ) = \frac{\sqrt{3}}{2}. \end{align*}

Now, we project \(u_r\) on \(x\) and \(y\) directions to get

\begin{align*} \amp u_x = u_r\, \cos(40^\circ) = 0.66.\\ \amp u_y = u_r\, \sin(40^\circ) = 0.56. \end{align*}

Therefore, our unit vector has the following representation.

\begin{equation*} \hat u = 0.66 \hat i + 0.56 \hat j + 0.5 \hat k. \end{equation*}

We should verify that it has magnitude of 1 by

\begin{equation*} \sqrt{0.66^2 + 0.56^2 + 0.5^2}, \end{equation*}

which is indeed 1 within the tolerance of the rounding. My answer is a little different than exact 1 since I had rounded off earlier.

Example 3.56. Magnitude and Direction of Force in First Quadrant.

A suitcase is draged by applying a force on the strap attached to the suitcase.

With respect to a Cartesian coordinate system that has the \(x \) axis along the horizontal direction and the \(y \) axis vertically up, the components of the force are \((F_x, F_y) = (12.0\text{ N}, 5.0\text{ N}) \text{,}\) where N stands for the unit Newton.

What are the magnitude and direction of the force? You can use the symbol \(F \) for the magnitude and \(\theta \) for the angle with respect to the \(x \) axis.

Answer.

\(F = 13.0\text{ N and } \theta = 22.6^{\circ} \text{ or } 0.395 \text{ rad}.\)

Solution.

Let \(F \) denote the magnitude of the force, i.e., equivalent of \(r \) of the polar form of the vector.

\begin{equation*} F = \sqrt{F_x^2 + F_y^2} = \sqrt{12.0^2 + 5.0^2} = 13.0 \end{equation*}

Putting the units back, we get the magnitude of the force, \(F = 13.0\text{ N}\text{.}\)

Leaving units out when doing calculations:

\begin{equation*} \tan\theta = \dfrac{F_y}{F_x} = \dfrac{5.0}{12.0} = 0.42 \end{equation*}

Inverting this, we get \(\theta = 22.6^{\circ} \text{ or } 0.395 \text{ rad}\text{.}\)

Example 3.58. Direction in the Second Quadrant.

A vector has \((A_x, A_y) = (-3, 1) \text{.}\) What is the direction of this vector with respect to the negative \(x \) axis?

Answer.

\(18.4^{\circ}\) clockwise from the negative \(x\)-axis.

Solution.

The angle using the arctangent formula gives the following.

\begin{align*} \theta \amp = \tan^{-1} \dfrac{A_y}{A_x} \\ \amp = \tan^{-1}\dfrac{1}{-3} = -18.4^{\circ}. \end{align*}

The negative sign refers to the clockwise direction into the second quadrant from the negative \(x \) axis direction as shown in the figure.

Example 3.61. Direction in the Third Quadrant.

A vector has \((A_x, A_y) = (-3, -2) \text{.}\) What is the direction of this vector with respect to the negative \(x \) axis?

Note arc-tangent will give you a positive angle, which is what you also get if the vector is pointed in the first quadrant. But, this vector is pointed in the third quardant. Therefore, you need to appropriately add or subtract \(180^{\circ}\text{.}\)

Answer.

\(33.7^{\circ}\) counterclockwise from the negative \(x\)-axis.

Solution.

The angle using the arctangent formula gives the following.

\begin{equation*} \theta = \tan^{-1} \dfrac{A_y}{A_x} = \tan^{-1}\dfrac{-2}{-3} = 33.7^{\circ}. \end{equation*}

Based on this calculation, if your answer is \(33.7^{\circ}\text{,}\) you would be implying that this angle is counterclockwise with respect to the positive \(x \)-axis, but that is wrong since the vector is pointed in the third quadrant, and the angle is with respect to the negative \(x\)-axis.

If you want to express the counterclockwise angle with respect to positive \(x\)-axis, you will need to add \(180^\circ\) to this value.

Example 3.64. Direction in the Fourth Quadrant.

A vector has \((A_x, A_y) = (3, -2) \text{.}\) What is the direction of this vector with respect to the positive \(x \) axis?

Note: the arc-tangent will give you a negative angle.

Answer.

\(33.7^{\circ}\) clockwise from the positiuve \(x\)-axis.

Solution.

The angle using the arctangent formula gives the following.

\begin{equation*} \theta = \tan^{-1} \dfrac{A_y}{A_x} = \tan^{-1}\dfrac{-2}{3} = -33.7^{\circ}. \end{equation*}

The negative sign refers to the clockwise direction into the fourth quadrant from the positive \(x \) axis direction as shown in the figure.

Exercises 3.2.5 Exercises

1. Magnitude and Direction of a Vector in 2D from Components.

The position of a box on the floor with respect to a corner of the room, taken to be the origin, and the walls which are taken to be \(x\) and \(y\)-axes, is given by the \((x,y) = (4.0\text{ m}, 3.0\text{ m})\text{.}\) What are the magnitude and direction of the position vector of the box?

Hint.

Just use the \((x,y) \rightarrow (r, \theta) \text{.}\)

Answer.

\(5.0\text{ m}, 36.9^{\circ}\text{ or } 0.644 \text{ rad} \) counterclockwise from \(+x\) axis.

Solution.

Let’s do the calculation leaving units out to get the magnitude.

\begin{equation*} r = \sqrt{x^2 + y^2} = \sqrt{4^2 + 3^2} = 5. \end{equation*}

Putting units back, the magnitude of the position vector will be be \(5.0\text{ m}\text{.}\)

For the direction, we compute angle \(\theta\) with \(x\)-axis.

\begin{equation*} \tan\theta = \dfrac{y}{x} = \dfrac{3}{4} = 0.75. \end{equation*}

Inverting this, we get \(36.9^{\circ}\text{ or } 0.644 \text{ rad}\text{.}\) Since point \((4,3)\) lies in the first quadrant, the direction is \(36.9^{\circ}\) counterclockwise with respect to the positive \(x\)-axis.

2. Components of a Vector from Magnitude and Direction in 2D.

A box is at a distance of \(5.0 \text{ m}\) from the origin. The direction of the location of the box makes an angle of \(30^{\circ} \) with respect to the direction of a wall taken to be the positive \(x \) axis. Another wall that is perpendicular to the \(x \) axis wall is taken to be the \(y \) axis. Find the \(x \) and \(y \) components of the position vector.

Hint.

Just use the \((r, \theta) \rightarrow (x,y) \text{.}\)

Answer.

\(x = 4.33\text{ m and } y = 2.50\text{ m}.\)

Solution.

Leaving units out, we have

\begin{equation*} x = r \cos\theta = 5.0 \cos 30^{\circ} = 4.33. \end{equation*}

Putting the units back, we get the \(x = 4.33\text{ m}\text{.}\) Similarly,

\begin{equation*} y = r \sin\theta = 5.0 \sin 30^{\circ} = 2.50. \end{equation*}

With units, \(y = 2.50\text{ m}\text{.}\)

3. Components of Velocity Vector of a Cricket Ball in a Horizontal-Vertical Plane.

A batsman strikes a cricket ball, which leaves the bat with a speed of \(20.0\text{ m/s}\text{,}\) and flies in the direction of \(60^{\circ}\) with respect to the horizontal direction. This means that the velocity vector has magnitude \(20.0\text{ m/s}\) and direction \(60^{\circ}\) with respect to the horizontal direction. Taking the horizontal direction as the \(x\)-axis and the vertical direction as the \(y \) axis, find \(x \) and \(y\) components of the velocity vector.

Hint.

Use the \((r, \theta) \rightarrow (x,y)\) transformation.

Answer.

\(v_x = 10.0\text{ m/s}\) and \(v_y = 17.3\text{ m/s}\text{.}\)

Solution.

Let \(\vec v \) be the symbol for the velocity vector, \(v \) the magnitude, \(\theta \) the angle with \(x\)-axis, and \(v_x \) and \(v_y\) the \(x \) and \(y\) components of the velocity vector. Doing the calculation leaving units out:

\begin{equation*} v_x = v \cos\theta = 20.0 \cos 60^{\circ} = 10.0. \end{equation*}

Putting the units back, we get the \(v_x = 10.0\text{ m/s}\text{.}\) Similarly, \(v_y = v \sin\theta\) gives \(v_y = 17.3\text{ m/s}\text{.}\)

4. Components of Velocity Vector of a Soccer Ball in a Horizontal-Vertical Plane.

A soccer ball is kicked in the direction \(30^{\circ}\) above the horizontal direction with speed \(15 \text{ m/s}\text{.}\) This means that the velocity vector of the ball has magnitude \(15 \text{ m/s}\) and direction \(30^{\circ}\) above the horizon. Find the coordinate representation of the velocity in a coordinate system in which \(x \) axis is along horizontal direction and positive \(y \) axis is pointed up.

Hint.

Use \(x = r\, \cos\, \theta\text{.}\)

Answer.

\(13 \text{ m/s}\text{,}\) \(7.5 \text{ m/s}\text{.}\)

Solution.

We just use the formulas that help us get components from magnitude and direction.

\begin{align*} \amp v_x = v\, \cos\, \theta = 15\text{ m/s}\, \cos\, 30^{\circ} = 13 \text{ m/s}.\\ \amp v_y = v\, \sin\, \theta = 15\text{ m/s}\, \sin\, 30^{\circ} = 7.5 \text{ m/s}. \end{align*}

5. Magnitude and Direction of Velocity from Components.

A velocity vector was found to have the following components, \(v_x = 30.0\text{ m/s}\) and \(v_y = 40.0\text{ m/s}\) with respect to a coordinate system in which \(x \) axis is along horizontal direction and positive \(y \) axis is pointed up. What are the magnitude and direction of the velocity vector? Describe your direction in words.

Hint.

Use \(r=\sqrt{x^2 + y^2} \) and \(\theta = \tan^{-1}(y/x) \text{.}\)

Answer.

\(\left( 50.0\text{ N},\ 53.1^{\circ} \right)\text{.}\) The direction is \(53.1^{\circ} \) above the horizon.

Solution.

Using the defining equations for magnitude \((v)\) and angle \((\theta)\) with \(x \) axis we get

\begin{align*} \amp v = \sqrt{v_x^2 + v_y^2} = \sqrt{30^2 + 40^2} = 50\text{ m/s},\\ \amp \theta = \tan^{-1}(v_y/v_x)= \tan^{-1}(40/30) = 53.1^{\circ}. \end{align*}

The angle is in the first quadrant since \(v_x >0 \) and \(v_y>0 \text{.}\) This means that the angle we found is above the horizon.

6. Magnitude and Direction of Velocity from Components - 2.

A velocity vector was found to have the following components, \(v_x = 30.0\text{ m/s}\) and \(v_y = -40.0\text{ m/s}\) with respect to a coordinate system in which the \(x \) axis is along horizontal direction and the positive \(y \) axis is pointed up. What are the magnitude and direction of the velocity vector? Describe your direction in words.

Hint.

Use \(r=\sqrt{x^2 + y^2} \) and \(\theta = \tan^{-1}(y/x) \text{.}\)

Answer.

\(\left( 50.0\text{ N},\ -53.1^{\circ} \right)\text{.}\) The direction is \(53.1^{\circ} \) below the horizon.

Solution.

Using the defining equations for magnitude \((v)\) and angle \((\theta)\) with \(x \) axis we get

\begin{align*} \amp v = \sqrt{v_x^2 + v_y^2} = \sqrt{30^2 + 40^2} = 50\text{ m/s},\\ \amp \theta = \tan^{-1}(v_y/v_x)= \tan^{-1}(-40/30) = -53.1^{\circ}. \end{align*}

The angle is in the fourth quadrant since \(v_x \gt 0 \) and \(v_y \lt 0 \text{.}\) This means that the angle we found is below the horizon. The arctan value came out negative - which means the angle is clockwise from the \(x \) axis as in the figure.

7. Practice Computing Magnitudes and Stating Directions.

Clearly, if you have the \((x,y) \) of an object, you can get the position vector by computing the \(r \) and \(\theta \text{.}\)

Draw position vectors of objects at the following coordinates and find their magnitudes and directions.

\((-1\text{ m}, 2\text{ m}) \text{,}\)
\((-3\text{ m}, -2\text{ m}) \text{,}\)
\((3\text{ m}, -1\text{ m}) \text{.}\)

Hint.

Use \((x,y) \rightarrow (r, \theta) \) equations.

Answer.

(a) \(\sqrt{5}\text{ m}, 63.4^{\circ} \) clockwise from the negative \(x \) axis, (b) \(\sqrt{13}\text{ m}, 33.7^{\circ} \) counterclockwise from the negative \(x \) axis, (c) \(\sqrt{10}\text{ m}, 18.3^{\circ} \) clockwise from the positive \(x \) axis.

Solution 1. a

The drawing is shown in the figure.

\begin{align*} \amp r = \sqrt{x^2 + y^2} = \sqrt{1^2 + 2^2} = \sqrt{5}\text{ m}.\\ \amp \theta = \tan^{-1}\left( \dfrac{y}{x}\right) = \tan^{-1}\left( \dfrac{2}{-1}\right) = -63.4^{\circ}. \end{align*}

The negative in the angle says that the angle is clockwise from the \(x \) axis. Since the \((-1, 2) \) is in the second quadrant, this angle will be with respect to the negative \(x \) axis. Therefore, the direction is \(63.4^{\circ} \) clockwise from the negative \(x \) axis.

Solution 2. b, c

Do them similarly. Make sure you state the direction as clockwise and counterclockwise from either positive or negative \(x \) axis.

8. Components of a Force Vector from Magnitude and Direction in First Quadrant.

A force vector \(\vec F \) has magnitude \(50\text{ N} \) and is pointed in the direction \(30^{\circ} \) North of East. Let \(x \) axis be pointed towards East and \(y \) axis towards North.

(a) Draw a figure to display this vector, stating the scale you used in your drawing.

(b) Find the \(x \) and \(y \) components, \(F_x \) and \(F_y \text{,}\) of this vector.

Hint.

The \((F_x, F_y) \) have the same relation to \((F, \theta) \) as do \((x,y)\) to \((r, \theta) \text{.}\)

Answer.

(b) \(43.3\text{ N},\ 25.0\text{ N} \)

Solution.

(a) The figure shows the drawing.

(b) The \((F_x, F_y) \) have the same relation to \((F, \theta) \) as do \((x,y)\) to \((r, \theta) \text{.}\)

\begin{align*} \amp F_x = 50\times \cos\, 30^{\circ} = 43.3\text{ N}.\\ \amp F_y = 50\times \sin\, 30^{\circ} = 25.0\text{ N}. \end{align*}

9. Components of a Force Vector from Magnitude and Direction in the Fourth Quadrant.

A force vector \(\vec F \) has magnitude \(50 \) N and is pointed in the direction \(30^{\circ} \) South of East. Let \(x \) axis be pointed towards East and \(y \) axis towards North.

(a) Draw a figure to display this vector, stating the scale you used in your drawing.

(b) Find the \(x \) and \(y \) components, \(F_x \) and \(F_y \text{,}\) of this vector.

Hint.

The \((F_x, F_y) \) have the same relation to \((F, \theta) \) as do \((x,y)\) to \((r, \theta) \text{.}\) Be mindful the quadrant and take care of signs of components accordingly.

Answer.

(b) \(43.3\text{ N},\ -25.0\text{ N} \)

Solution.

(a) Figure 3.70 shows the drawing.

(b) The \((F_x, F_y) \) have the same relation to \((F, \theta) \) as do \((x,y)\) to \((r, \theta) \text{.}\)

When you have a vector in a quadrant other than the first quadrant, you need to make sure you take care of the sign of resulting components by observing where the vector projects on the axes.

Here, since the vector is in the fourth quadrant, it will project on the positive \(x \) and on the negative \(y\text{.}\) That will mean \(F_x \gt 0 \) and \(F_y \lt 0\text{.}\)

\begin{align*} \amp F_x = 50\times \cos\, 30^{\circ} = 43.3\text{ N}.\\ \amp F_y = -50\times \sin\, 30^{\circ} = -25.0\text{ N}. \end{align*}

10. Magnitude and Direction of a Force Vector from Components in the Second Quadrant.

The \(x \) and \(y\) components of a force vector are given to be \(F_x = -30\text{ N}\) and \(F_x = 40\text{ N}\text{.}\) What are the magnitude and direction of this force?

Hint.

use \((x,y)\) to \((r, \theta)\) and interpret the angle.

Answer.

\(F = 50\text{ N}\text{,}\) \(53.1^{\circ}\) clockwise from the negative \(x \) axis

Solution.

The magnitude is

\begin{equation*} F = \sqrt{30^2 + 40^2} = 50\text{ N}. \end{equation*}

Since the point \(( -30, 40) \) is in the second quadrant, we will get angle with respect to the negative \(x \) axis.

\begin{equation*} \theta = \tan^{-1}\left( \dfrac{40}{-30}\right) = -53.1^{\circ}. \end{equation*}

The negative angle means we need to go clockwise. Thus, the direction is \(53.1^{\circ}\) clockwise from the negative \(x \) axis.

11. Detemining Components of Vectors.

Determine the \(x\) and \(y\)-components of the following vectors in the \(xy\)-plane of a particular coordinate system. Here, the terms counterclockwise and clockwise refer to the rotation direction as you look from the side of the positive \(z\)-axis.

A force of magnitude \(10\) N in the direction of \(30^{\circ}\) counterclockwise from the positive \(x\)-axis direction.
A force of magnitude \(10\) N in the direction of \(30^{\circ}\) clockwise from the negative \(x\)-axis direction.
A force of magnitude \(10\) N in the direction of \(30^{\circ}\) counter-clockwise from the positive \(y\)-axis direction.
A force of magnitude \(10\) N in the direction of \(30^{\circ}\) clockwise from the negative \(y\)-axis direction.

Solution 1.

The components of vectors with respect to Cartesian coordinates is best obtained by first drawing a diagram and be clear about the angles rather than using some canned formulas. You have to be very alert about positive and negative values of the components. Although the magnitude is always positive, the components can be positive or negative depending upon the projection on the axes as we will see in these exercises.

Solution 2. a

\begin{align*} \amp F_x = F \cos\theta = 8.66\ \textrm{N}\\ \amp F_y = F \sin\theta = 5\ \textrm{N} \end{align*}

Solution 3. b

\begin{align*} \amp F_x = -F \cos\theta = -8.66\ \textrm{N}\\ \amp F_y = F \sin\theta = 5\ \textrm{N} \end{align*}

Solution 4. c

\begin{align*} \amp F_x = -F \sin\theta = - 5\ \textrm{N}\\ \amp F_y = F \cos\theta = 8.66\ \textrm{N} \end{align*}

Solution 5. d

\begin{align*} \amp F_x = -F \sin\theta = - 5\ \textrm{N}\\ \amp F_y = -F \cos\theta = - 8.66\ \textrm{N} \end{align*}

12. Magnitudes and Directions from Components.

Determine the magnitudes and directions of the following vectors given in the component form with respect to a particular Cartesian coordinate system, where the positive \(x\)-axis points to the East, the positive \(y\)-axis points to the North and the positive \(z\)-axis points vertically up. Make sure you give the units for the magnitudes of the vectors if appropriate. From any angle(s) you calculate, state the physical direction in space for each vector. Here m is the unit meter.

\((3\ \textrm{m})\ \hat u_x + (4\ \textrm{m})\ \hat u_y\text{.}\)
\((-3\ \textrm{m})\ \hat u_x + (4\ \textrm{m})\ \hat u_y\text{.}\)
\((-3\ \textrm{m})\ \hat u_x + (-4\ \textrm{m})\ \hat u_y\text{.}\)
\((3\ \textrm{m})\ \hat u_x + (-4\ \textrm{m})\ \hat u_y\text{.}\)

Solution 1.

Finding magnitudes of the given vectors is quite straightforward and easily written by giving one number and the unit. But for the directions of the vectors we need to choose a convention. In these problems, since all the vectors are in the \(xy\)-plane, to indicate the direction I will choose the counterclockwise angle of the vector with respect to the positive \(x\)-axis as you look from the positige \(z\)-axis. In other planes, you can find similar angles. Let us denote the vectors by symbol \(\vec d\text{.}\)

Solution 2. a

The magnitude = \(\sqrt{d_x^2 + d_y^2} = 5\) m. Since the angle is in the first quadrant, no adjustment from the value obtained from the calculator is needed.

\begin{equation*} \theta =\tan^{-1} \left( \frac{4}{3} \right) \approx 53^{\circ}. \end{equation*}

Solution 3. b

The magnitude = \(\sqrt{d_x^2 + d_y^2} = 5\) m. To obtain the angle we can use the right-angled triangle shown in the figure. The arc-tangent will again be the trig function we need. Suppose we plug numbers in the calculator as

\begin{equation*} \theta = \tan^{-1} \left( \frac{4}{-3} \right) \approx - 53^{\circ}. \end{equation*}

We find that the angle is negative. We can state this angle several ways. One way os to state that the angle is \(53^{\circ}\) clockwise from the negative \(x\) axis. Another way to state this angle to convert this information to the counterclocwise angle with respect to the positive \(x\)-axis direction. If we want the counterclockwise angle with respect to the positive \(x\) axis, we will need to add \(180^{\circ}\) to this value. Let us call that angle \(\theta'\) to distinguish the two values.

\begin{equation*} \theta' = \ - 53^{\circ} + 180^{\circ} = 127^{\circ}. \end{equation*}

Solution 4. c

The magnitude = \(5\) m and the counterclockwise angle from the positive \(x\) axis direction \(\theta' = 233^{\circ}\text{.}\) [Verify these].

Solution 5. d

The magnitude = 5 m and the counterclockwise angle from the positive \(x\) axis direction \(\theta' = 307^{\circ}\text{.}\) [Verify these].

13. Magnitude and Directions of Three-Dimensional Vectors.

Determine the magnitudes and directions of the following vectors given in component form with respect to a particular Cartesian coordinate system, where the positive \(x\)-axis points to the East, the positive \(y\)-axis points to the North and the positive \(z\)-axis points vertically up. Make sure you give units for the magnitudes of the vectors if appropriate. From any angle(s) you calculate, state the physical direction in space for each vector. Here m is the unit meter.

\((3\ \textrm{m})\ \hat u_x + (4\ \textrm{m})\ \hat u_y + (12\ \textrm{m})\ \hat u_z\text{.}\)
\((-3\ \textrm{m})\ \hat u_x + (4\ \textrm{m})\ \hat u_y + (12\ \textrm{m})\ \hat u_z\text{.}\)
\((3\ \textrm{m})\ \hat u_x + (-4\ \textrm{m})\ \hat u_y + (12\ \textrm{m})\ \hat u_z\text{.}\)
\((3\ \textrm{m})\ \hat u_x + (4\ \textrm{m})\ \hat u_y + (-12\ \textrm{m})\ \hat u_z\text{.}\)
\((-3\ \textrm{m})\ \hat u_x + (-4\ \textrm{m})\ \hat u_y + (-12\ \textrm{m})\ \hat u_z\text{.}\)

Solution. a

In this exercise all the vectors are in three-dimensional space. We will need to specify two angles which are usually the polar (\(\theta\)) and azimuthal (\(\phi\)) angles of the spherical coordinate system associated with the given Cartesian coordinates. Let us denote the vectors by the symbol \(\vec d\text{.}\)

Magnitude, \(d = \sqrt{d_x^2 +d_y^2 + d_z^2} = 13\) m. The polar angle \(\theta\) for this vector is

\begin{equation*} \theta = \tan^{-1}\left( \frac{d_z}{\sqrt{d_x^2 + d_y^2}}\right) = 67.4^{\circ}, \end{equation*}

and the azimuthal angle is

\begin{equation*} \phi = \tan^{-1}\left( \frac{d_y}{d_x}\right) = 53^{\circ}. \end{equation*}

We leave the other exercises for the student to work out. Pay particular attention to different quadrants in the \(xy\)-plane for the azimuthal angle.

14. Practice with a Friend: Find Unit Vectors in the Direction of Given Vectors.

Find unit vectors in the directions of the following vectors. (a) \((100\ \textrm{N})\ \hat u_x + (-10\ \textrm{N})\ \hat u_y + (100\ \textrm{N})\ \hat u_z\text{,}\) (b) \((3\ \textrm{m})\ \hat u_x + (4\ \textrm{m})\ \hat u_z\text{,}\) (c) \((30\ \textrm{m})\ \hat u_y + (4\ \textrm{m})\ \hat u_z\text{,}\) (d) \((2\ \textrm{N})\ \hat u_x + (3\ \textrm{N})\ \hat u_y + (4\ \textrm{N})\ \hat u_z\text{.}\)

15. Practice with a Friend: Angles Vectors Make with Cartesian Axes.

Find the angles each vector makes with positive \(x\text{,}\) \(y\) and \(z\)-axes.

\(-3\hat u_x +2 \hat u_y + 4\hat u_z\text{,}\)
\(3\hat u_x -2 \hat u_y + 4\hat u_z\text{,}\)
\(3\hat u_x + 2 \hat u_y - 4\hat u_z\text{,}\)
\(\displaystyle 3\hat u_x -2 \hat u_y - 4\hat u_z\)
\(-3\hat u_x -2 \hat u_y - 4\hat u_z\text{.}\)

Prev Top Next