Wave Functions

Section 14.7 Wave Functions

A traveling or progressive wave, which we have been calling simply a wave, represents the movement of a disturbance from one place to another without the actual movement of the underlying medium itself.

The property characterizing the disturbance depends on the nature of the wave. For instance, in the case of a mechanical wave or sound wave, the disturbance refers to the displacement of the particles of the medium from their equilibrium positions as we have seen above. In the case of the electromagnetic wave, the disturbance refers to is the change in the electric and magnetic fields in space. In quantum mechanics, it can get very abstract.

The function that describes how the disturbance, representing a wave, varies both in space and time is called wave function. We have used \(y(x,t)\) for the transverse vibration modes on a string to represent wave on a string. But, the use of \(y\) would be misleading if we want to represent a wave in a three-dimensional situation, such as sound wave. Therefore, often we will use Greek letter \(\psi\) (read: si as in the word “sigh” ) for a wave function. Thus, wave on a string laid out along \(x\) axis will be \(\psi(x,t)\) with \(\psi\) standing for the transverse displacement and pressure wave in air will be \(\psi(x,y,z,t)\) with \(\psi\) denoting the pressure difference \(\Delta p\) from the ambient pressure.

When a wave is moving in a three-dimensional space, such as sound produced by a speaker, we can speak of wave fronts. A wave front of a wave at some time \(t\) is a surface representing the displacement of particles at that instant. We will talk about two special wavefronts - plane wavefronts and spherical wave fronts - that we use in analytic work with waves.

In this section, we will present three examples of wave functions that are very useful for analytic purposes.

Subsection 14.7.1 Plane Waves

A plane wave is a simple three-dimensional wave where the wave travels in a straight line, which is usually taken to be one of the Cartesian axes. Furthermore, wave function has the same value throughout any plane normal to the direction of wave. The wavefronts of such waves are planar and not curved.

Figure 14.20. A plane wave has same wave amplitude in the entire plane. It is a volume wave. Although it looks similar to the wave on a string it is three-dimensional rather than one-dimensional.

If a plane wave is traveling along \(x\) axis, then on each plane parallel to the \(yz\) plane, the wave displacement has the same value (see Figure 14.20), which oscillates with time. Therefore, the wave function for a plane wave traveling towards the positive \(x\) axis would not depend on the \(y\) or \(z\) coordinates of the point.

Plane waves are also sinusoidal. Therefore, the plane wave corresponding to a wave of wavelength \(\lambda\) and frequency \(f\) traveling towards the positive \(x\) axis will have the following wavefunction.

\begin{equation} \psi(x,y,z,t) = A\cos\left( \dfrac{2\pi}{\lambda} x - 2\pi f t + \phi\right),\tag{14.45} \end{equation}

where \(\phi\) is the phase constant. Of course, the wave going towards the negative \(x\) axis will be

\begin{equation} \psi(x,y,z,t) = A\cos\left( \dfrac{2\pi}{\lambda} x + 2\pi f t + \phi\right).\tag{14.46} \end{equation}

The speed of the wave will be given by the fundamental relation.

\begin{equation} v = \lambda f.\tag{14.47} \end{equation}

These wavefunctions are similar to the wavefunction of wave on a string laid out along \(x\) axis, but there is a big difference - plane waves are waves in three-dimensional space and cover the entire space, not just along string.

We can write a more general formula for a plane wave moving in an arbitrary direction, say the direction of the unit vector \(\hat u\text{.}\) Let us introduce a vector of length equal to the wavenumber \(k\) and the direction of \(\hat u\text{.}\)

We will denote this vector by \(\vec k\text{.}\)

\begin{equation} \vec{k} = k\, \hat u,\tag{14.48} \end{equation}

where \(k\text{,}\) you may recall is related to the inverse of wavelength \(\lambda\text{.}\)

\begin{equation} k = \dfrac{2\pi}{\lambda}. \tag{14.49} \end{equation}

Vector \(\vec k\) is called wave vector. Let us denote position of an arbitrary point P\((x,y,z)\) by vector \(\vec r\) from origin to that point.

\begin{equation} \vec{r} = x\, \hat i + y\, \hat j + z\, \hat k,\tag{14.50} \end{equation}

where \(\hat i,\ \hat j,\ \hat k\) are the usual unit vectors along the Cartesian axes. Using wave vector and the position vector, we can write the wave function of a plane wave more generally as

\begin{equation} \psi(x,y,z,t) = A\cos\left( \vec k \cdot \vec r - 2\pi f t + \phi\right).\tag{14.51} \end{equation}

Subsection 14.7.2 Spherical Waves

If energy from a source of wave spreads out radially in all three directions, then, wave amplitude will decrease with distance and it is no longer be appropriate to think of these waves as plan waves. As shown in Figure 14.21, the wavefronts of these waves are spherical in shape, and therefore they are called spherical waves.

Figure 14.21. Spherical wave fronts emanating from a source at the center, the drawing on the left. A cross-section is shown in the drawing on the right. The amplitude drops with the radial distance from the source. The drop off of the amplitude is shown with thickness of lines in the dawing on the right.

Since spherical wave spreads out symmetrically in all directions, it is independent of the angular coordinates \(\theta\) and \(\phi\) of spherical coordinates with origin at the source. To describe a spherical wave of wavelength \(\lambda = 2\pi/k\) and frequency \(f = \omega/2\pi\text{,}\) we use spherical radial distance \(r\) with origin at the source.

\begin{equation} \psi(r, t) = \dfrac{A}{r}\cos(kr-\omega t + \delta),\tag{14.52} \end{equation}

where \(\delta\) is the phase constant. Notice that wave function varies inversely with distance \(r\) from the source, which is at the origin here. This inverse distance relation is important for energy conservation as same amount energy in wave must pass through two envelops, say at \(r_1\) and \(r_2\) and energy in a wave is proportional to the square of the wave amplitude. We will study this question later.

Subsection 14.7.3 Wave Pulses

So far we have discussed waves of infinite extent such as the sinusoidal and plane waves. Sinusoidal waves are given by a sine or a cosine function of space and time. For these types of waves, the displacement oscillates in time according to a combination of sine and cosine functions of time having a definite frequency. Mathematically, to be periodic in space and time, the sinusoidal functions must have a domain that cover the entire space and entire time, viz. \(-\infty \lt x \lt \infty\) and \(-\infty \lt t \lt \infty\) for a wave traveling along \(x\)-axis. These waves are idealization of the situations encountered in real life.

Real waves, such as water waves, a pulse traveling on a string, or sound of a drum are not sinusoidal waves. They can be of any shape. For instance, suppose a very long taut string is given a snap at one end once while the end is held fixed in one place to provide tension in the string (Figure 14.22). This results in a bump in the string, which moves towards the other end. This is also a wave, although it does not look like the sine or cosine function. We call such a wave a pulse.

Figure 14.22. Generation and movement of a wave pulse on a string. Insteach of continuously shaking the end, you just givbe it a snap and let the pulse go.

How would you represent a pulse mathematically? There are a variety of ways to do that. You would want a shape to move in time. Say, we want a Gaussian shape, then we might try the following for the pulse on a string along \(x\) axis.

\begin{equation} \psi(x,t) = A \exp{ \left[ - \dfrac{(x-vt)^2}{2\sigma^2} \right] },\tag{14.53} \end{equation}

where parameter \(\sigma\) controls the width of the Gaussian - small \(\sigma\) will mean highly peaked and large \(\sigma\) will mean a more spreadout Gaussian. At instant \(t\text{,}\) the Gaussian will be centered at \(x=vt\text{.}\)

Similarly, suppose you turn a Laser on for a very brief period, you would get a pulse of light wave. Or, if you hit a piano key, there again you will get a pulse of sound wave. In these cases, you produce waves of some particular frequency, but let it last only for a short period of time - these periods often contain tens to hundreds of cycles of the wave. Since the cycles do not last for ever, mathematically, they are not really sinusoidal, but sometimes, it is okay to treat them as if they were purely sinusoidal or plane waves. These waves are called wavetrains. In a future course, you might learn Fourier anlaysis and there you will learn how to better analyze them analytically.

Example 14.23. Determining Wave Function of a Plane Wave from Given Characteristics.

A pressure plane wave of wavelength 3 cm and speed 350 m/s travels through a medium of density \(1.2\text{ kg/m}^3\) towards positive \(y\) axis of a Cartesian coordinate system with an amplitude of \(5.0\times 10^{-4}\text{ Pa}\text{.}\) Assume that at \(t=0\text{,}\) the wave function at \(y=0\) has the value equal to its amplitude. Write the wave function for this wave.

Answer.

\(5.0\times 10^{-4}\text{ Pa}\ \cos( 209\, y - 73,300\, t)\)

Solution.

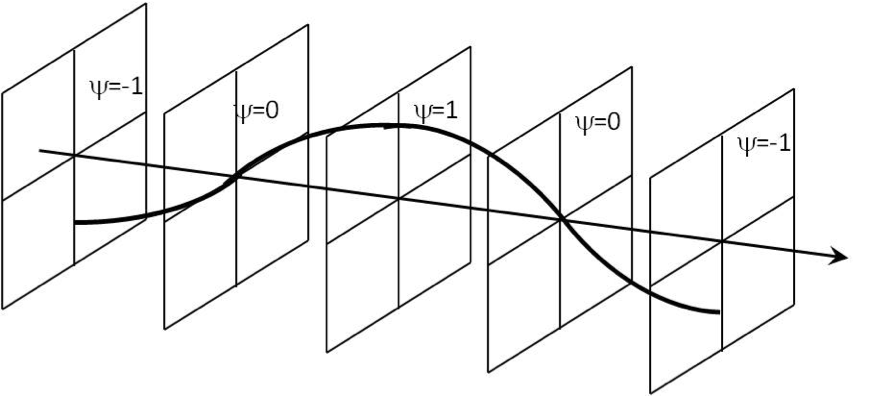
Since the wave is moving towards the positive \(y\) axis, the functional form of the wave will be

\begin{equation*} \psi(y,t) = A\cos(ky - \omega t + \phi). \end{equation*}

Since at \(t=0\) and \(y=0\text{,}\) \(\psi=A\text{,}\) we must have \(\phi=0\text{.}\) Therefore, we have

\begin{equation*} \psi(y,t) = A\cos(ky - \omega t). \end{equation*}

In this expression, \(A=5.0\times 10^{-4}\text{ Pa}\text{,}\) and we need to find the values of \(k\) and \(\omega\) from the given information.

\begin{align*} k \amp = \frac{2\pi}{\lambda} = \frac{2\pi}{0.03} = 209.4\text{ m}^{-1}.\\ \omega \amp = k v= 209.4 \times 350 = 73,300\text{ sec}^{-1}. \end{align*}

Therefore, the wave function is

\begin{equation*} \psi(y,t) = 5.0\times 10^{-4}\text{ Pa}\ \cos( 209\, y - 73,300\, t), \end{equation*}

where \(y\) is in \(m\) and \(t\) in \(sec\text{.}\)

Exercises 14.7.4 Exercises

1.

A spherical sound wave wave is given by the following function.

\begin{equation*} \psi(r,t) = \frac{4}{r} \cos\left(10 r - 200 t + \frac{\pi}{2} \right) \end{equation*}

where \(r\) is in cm, \(t\) in seconds and \(\psi\) in \(N/m^2\text{.}\) Here \(r\)is the spherical radial coordinate of a space point \((x,y,z)\) with \(r=\sqrt{x^2+y^2+z^2}\text{.}\)

(a) Find the amplitude at following points \((x,y,z)\text{.}\) (i) (0,0,1), (ii) (0,1,0), (iii) (1,0,0), (iv) (1,1,0), (v) (1,1,1), (vi) (-1,1,1), (v)(1,-1,1), (vi) (-1,-1,1).

(b) What are the wavelength, frequency, and speed of the wave?

Solution 1. a

Amplitude of the spherical wave is \(\frac{4}{r}\text{.}\) Therefore, we just need to find \(r\) of the space points given. The radial coordinate for the points are:

(i) \(1\text{,}\) (ii) \(1\text{,}\) (iii) \(1\text{,}\) (iv) \(\sqrt{2}\text{,}\) (v) \(\sqrt{3}\text{,}\) (vi) \(\sqrt{3}\text{,}\) (v) \(\sqrt{3}\text{,}\) (vi) \(\sqrt{3}\text{.}\)

Therefore amplitudes in units of \(N/m^2\) are (i) \(4\text{,}\) (ii) \(4\text{,}\) (iii) \(4\text{,}\) (iv) \(4/\sqrt{2}\text{,}\) (v) \(4/\sqrt{3}\text{,}\) (vi) \(4/\sqrt{3}\text{,}\) (v) \(4/\sqrt{3}\text{,}\) (vi) \(4/\sqrt{3}\text{.}\)

Solution 2. b

From the oscillating part \(\cos\left(10 r - 200 t + \frac{\pi}{2} \right) \) of the wavefunction we get

\begin{equation*} k = 10\,\text{m}^{-1},\ \ \omega = 200\,\text{s}^{-1}. \end{equation*}

Therefore, wavelength is

\begin{equation*} \lambda = \frac{2\pi}{k} = 0.2\,\pi\,\text{m}. \end{equation*}

Frequency is obtained from the angular frequenc by

\begin{equation*} f = \frac{\omega}{2\pi} = \frac{100}{\pi}\,\text{Hz}. \end{equation*}

Speed of the wave is \(v = \lambda f = \omega/k\) . Therefore

\begin{equation*} v = \omega/k = 200/10 = 20\,\text{m/s}. \end{equation*}

Prev Top Next