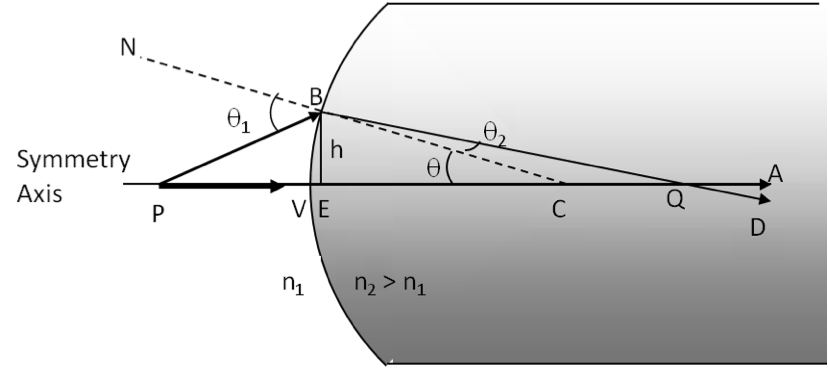
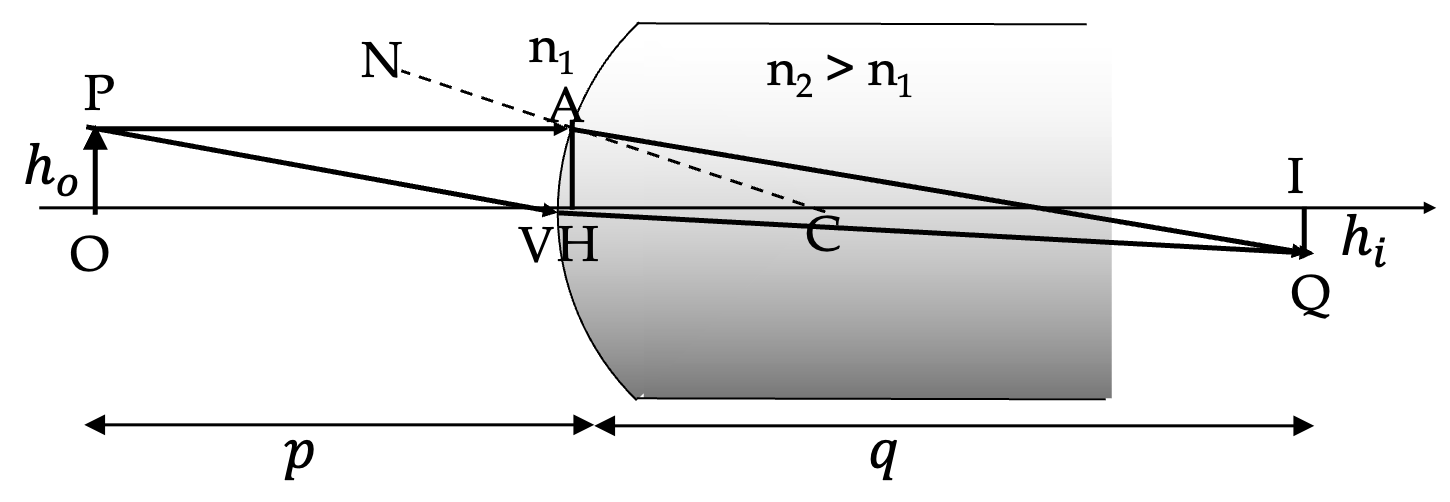
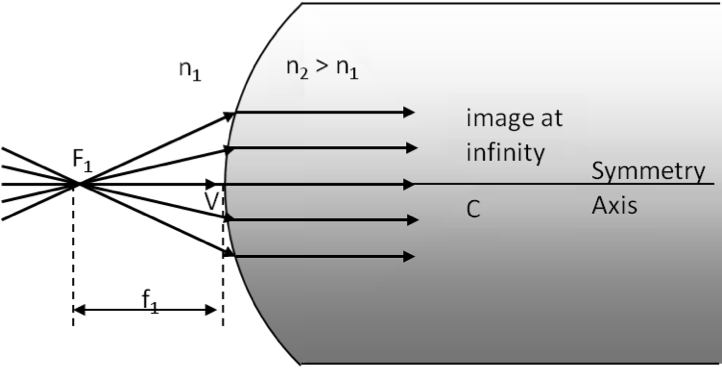
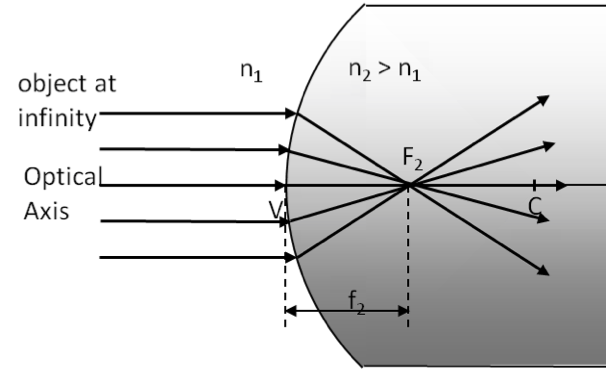
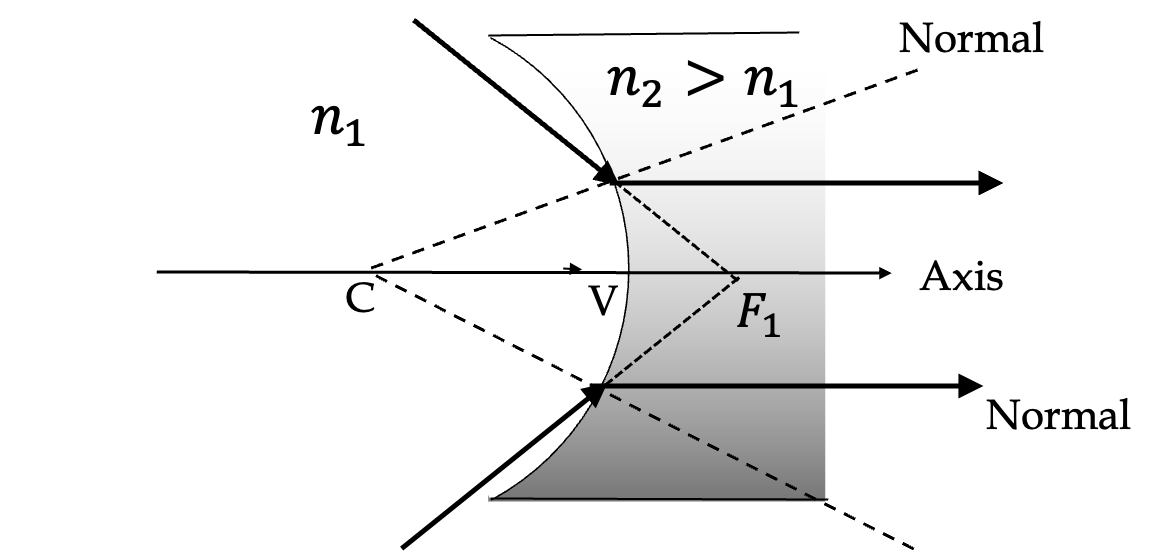
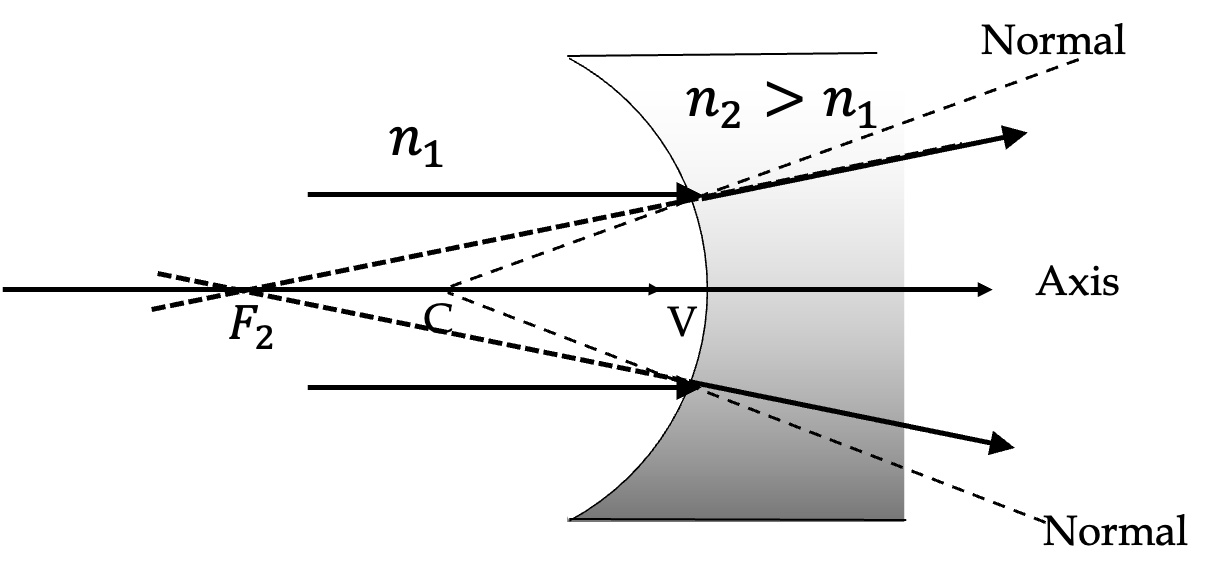
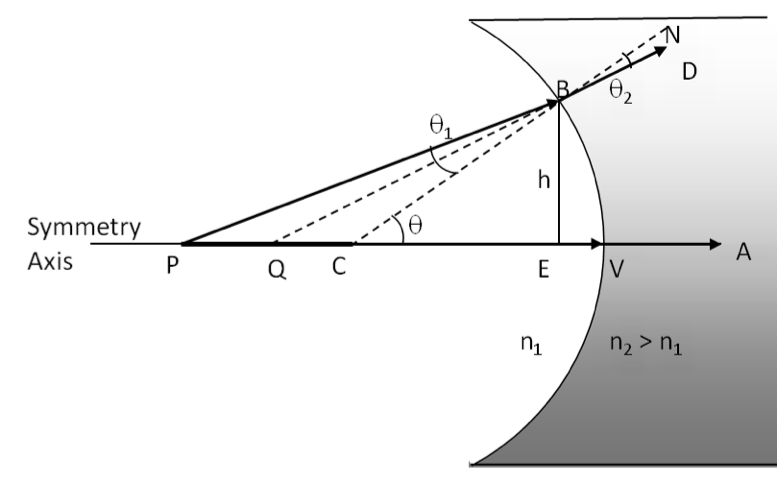
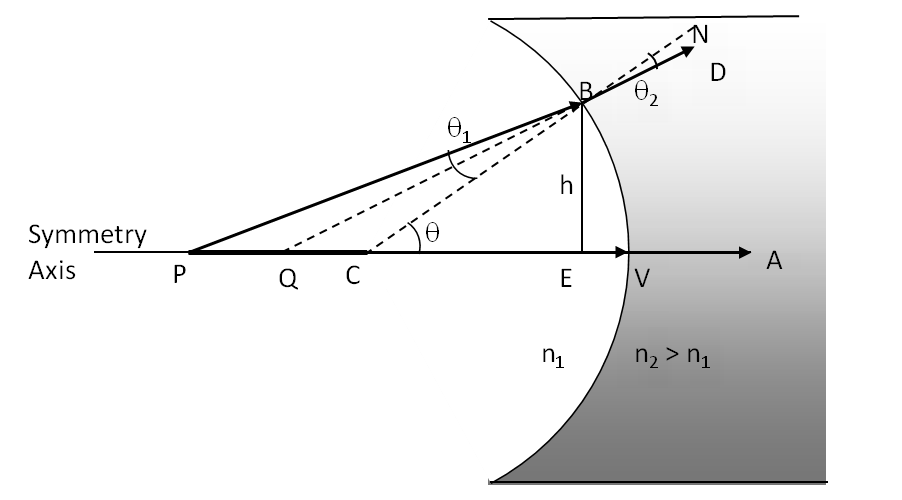
Example 44.39. Image by Refraction at a Convex Surface.
An object is located in air \(240\, \text{cm}\) from the vertex of a convex surface made of glass with a radius of curvature \(60\, \text{cm}\text{.}\) Where does the image by refraction form and what are its orientation and magnification?
Answer.
\(q = 360\, \text{cm}\text{,}\) \(M_T = -6\text{.}\)
Solution.
In this problem we have
\begin{equation*}
R = +60\:\textrm{cm},\ \ p = 240\:\textrm{cm},\ \ n_1 = 1,\ \ n_2 = 1.5.
\end{equation*}
Using these values in the equation for refraction at convex surface gives
\begin{equation*}
\frac{1}{240} + \frac{1.5}{q} = \frac{(1.5-1)}{60} = \frac{1}{120}.
\end{equation*}
Therefore
\begin{equation*}
\frac{1.5}{q} = \frac{1}{120} - \frac{1}{240} = \frac{1}{240}.
\end{equation*}
Hence, \(q = 360\,\text{cm}\text{.}\)
The orientation and magnification is contained in \(M_T\text{.}\) Since we already know \(p\) and \(q\text{,}\) we immediately get the magnification.
\begin{equation*}
M_T = -\frac{q}{p} = -\frac{360}{60} = -6.
\end{equation*}
The image is inverted with respect to the object (since \(M_T \lt 0\)) and \(6\)-times as large.