Displacement Current

Section 42.1 Displacement Current

The four basic laws of electricity and magnetism were discovered experimentally. While studying them James Clerk Maxwell(1831-1879) discovered some logical inconsistencies. The source of inconsistencies turned out to be the incompleteness of Ampere’s law. Recall that according to Ampere’s law the circulation of magnetic field around a loop C is proportional to the current passing through any surface (S) whose boundary is the loop C itself.

\begin{equation} \oint_C \vec B\cdot d\vec l = \mu_0 I_{\text{enc}} \ \ \text{(independent of surface)}.\tag{42.1} \end{equation}

Although, there are infinitely many surfaces that can be attached to any loop, it is important to realize that Ampere’s law stated in Eq. (42.1) is independent of the choice of surface as illustrated in Figure 42.1.

Figure 42.1. Three open surfaces \(S_1\text{,}\) \(S_2\text{,}\) \(S_3\) attached to the same loop C. For steady current in the wire all three surfaces will give the same value for the enclosed enclosed current consistent with the Ampere’s law.

Now, consider the following experiment shown in Figure 42.2.

Figure 42.2. Applying Ampere’s law in a non-steady situation results into inconsistent results! The currents through S1 and S2 are not equal although they have the same boundary loop C.

Connect a parallel plate capacitor to an EMF source \(V\text{.}\) When the switch is closed, a time-dependent current develops in the wire. Let us now apply Ampere’s law to loop C shown at a time before the capacitor is fully charged such that \(I \ne 0\text{.}\) With the surface \(S_1\text{,}\) you get a non-zero value for the enclosed current \(I\text{,}\) while with surface \(S_2\) you get a zero for the enclosed current since no current passes through it.

\begin{equation*} \oint_C \vec B\cdot d\vec l = \left\{ \begin{array}{ll} \mu_0 \ \ \amp \text{if you use surface}\ S_1\\ 0 \amp \text{if you use surface}\ S_2 \end{array} \right. \end{equation*}

Clearly, Ampere’s law does not work here. You might have already suspected this because Ampere’s law requires a steady current, while the current in this experiment is changing with time and not steady at all.

How can we modify Ampere’s law so that it will work in all situations? This question was answered by James Clerk Maxwell. The experiment with the capacitor suggests a solution for this problem. In Figure 42.2, you will notice that, while current passes through surface \(S_1\text{,}\) a time-dependent electric field passes through \(S_2\text{.}\) So, it would be tempting to correct Eq. (42.1) by adding the flux of E-field through a surface in addition to \(I_{\text{enc}}\text{.}\) But this will not work because when the capacitor is fully charged you get another inconsistency: although there will be no current through \(S_1\text{,}\) there will still be a non-zero flux of E-field through \(S_2\text{.}\)

Maxwell suggested that rather than adding the electric flux, you will need the rate of change of electric flux to correct the Ampere’s law. He suggested the form of the additional contribution to the real current \(I\) called the displacement current \(I_d\text{.}\)

\begin{equation} \oint_C \vec B\cdot d\vec l = \mu_0 \left( I_{\text{enc}} + I_{\text{d,enc}} \right) \ \ \text{(independent of surface)}.\tag{42.2} \end{equation}

The displacement current \(I_d\) is supposed to be the contribution from the changing electric flux through the surface attached to the loop for the circulation integral on theleft side of this equation. Specifically, the displacement current is defined to be

\begin{equation} I_d = \epsilon_0 \frac{d\Phi_E}{dt}, \tag{42.3} \end{equation}

where \(\epsilon_0\) is the permittivity of free space, and \(\Phi_E\) the electric flux defined as

\begin{equation} \Phi_E = \iint_{\text{Surface,S}}\vec E \cdot d\vec A. \tag{42.4} \end{equation}

Note that since surfaces attached to the loop are not closed the electric flux is not equal to the \(Q_{enc}/\epsilon_0\) as would be expected for the electric flux through a closed surface according to Gauss’s law.

Recall the relationship of current \(I\) to the current density vector .

\begin{equation*} I = \iint_S \vec J\cdot d\vec A. \end{equation*}

Similarly, we also define a displacement current density vector \(\vec J_d\text{.}\)

\begin{equation} I_d = \iint_S \vec J_d\cdot d\vec A. \tag{42.5} \end{equation}

Putting Eq. (42.5) in Eq. (42.3) and using Eq. (42.4) we deduce

\begin{equation*} \vec J_d = \epsilon_0 \frac{\partial \vec E}{\partial t} \end{equation*}

The modified Ampere’s law, Eq. (42.2) also explains correctly even the time-dependent situations depicted in Figure 42.2 - the surface \(S_1\) has contribution from current and the surface \(S_2\) has equal contribution from the displacement current of the time-varying electric field. We will call the modified Ampere’s law as Ampere-Maxwell’s law.

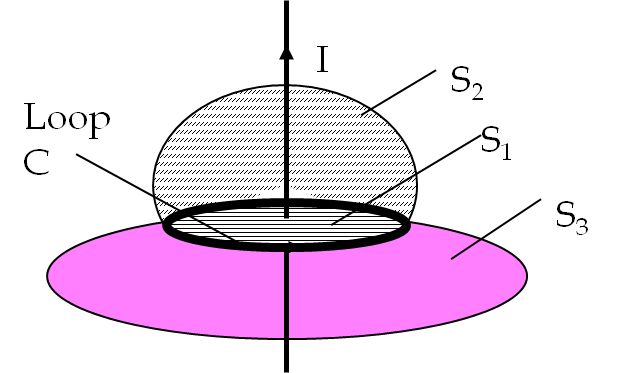
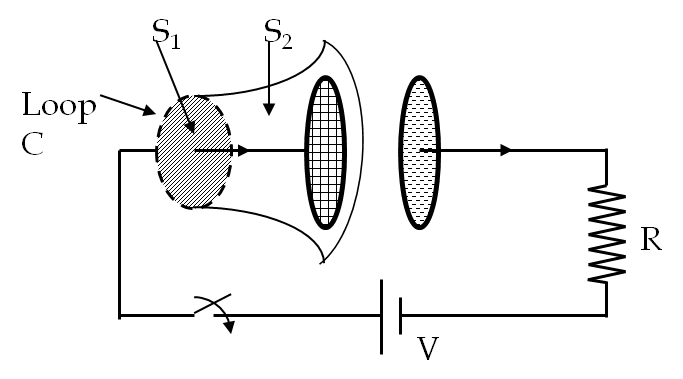
Example 42.3. Displacement Current in a Charging Capacitor.

A parallel-plate capacitor \(C\) whose plates are separated by a distance \(d\) is connected to a resistor \(R\) and a battery of voltage \(V\text{.}\) The current starts to flow at \(t=0\text{.}\)

(a) Find the displacement current density between the capacitor plates at time \(t\text{.}\)

(b) From the displacement current between the plates find the current in the circuit.

Answer.

(a) \(\frac{V_0}{RA} \: e^{-t/RC}\text{,}\) (b) \(\frac{V_0}{R} \: e^{-t/RC} \text{.}\) (c) \(\frac{V_0}{R} \: e^{-t/RC}\text{.}\)

Solution.

(a) The voltage between the plates at time \(t\) is given by

\begin{equation*} V_C = \frac{1}{C} q(t) = V_0\left( 1 - e^{-t/RC}\right). \end{equation*}

Let the \(z\)-axis point from the positive plate to the negative plate. Then, the \(z\)-component of the electric field between the plates as a function of time t is

\begin{equation*} E_z(t) = \frac{V_0}{d}\left( 1 - e^{-t/RC}\right). \end{equation*}

Therefore the \(z\)-component of the displacement current density between the plates is

\begin{align*} J_{dz}\amp = \epsilon_0\frac{\partial E_z(t)}{\partial t} \\ \amp =\epsilon_0\frac{V_0}{d}\times\frac{1}{RC}\: e^{-t/RC} = \frac{V_0}{RA} \: e^{-t/RC}, \end{align*}

using \(C = \epsilon_0 A/d\text{.}\)

(b) Integrating \(J_d\) over the area of cross-section, which is an area equal to the area of the plate, will yield the current.

\begin{equation*} I_d = \int\int\vec J_d \cdot d\vec A = \frac{V_0}{R} \: e^{-t/RC}. \end{equation*}

(c) From the analysis of an \(RC\)-circuit in a precious chapter, the current into the capacitor is found decrease with time after the circuit is closed as

\begin{equation*} I = \frac{V_0}{R} \: e^{-t/RC}. \end{equation*}

This current is same as \(I_d\) we found in (b).

Example 42.4. Computing Displacement Current Density and Current Between Plates of a Parallel Capacitor.

Voltage across a parallel plate capacitor with area \(A =800 \text{ cm}^2\) and separation \(d = 2 \text{ mm}\) varies sinusoidally as \(V = (15\ \text{mV})\cos(150\: t)\text{,}\) where \(t\) is in sec. (a) Find the displacement current density between the plates. (b) Find the displacement current between the plates.

Answer.

(a) \(9.96\times 10^{-9}\ (\text{A/m}^2)\ \sin(150\ t)\text{,}\) (b) \(\left( 7.97\times 10^{-10}\: \text{A}\right) \: \sin(150\ t)\text{.}\)

Solution.

(a) The displacement current density is given by \(\vec J_d = \epsilon_0\partial \vec E/\partial t\text{,}\) and the magnitude of the electric field between the two plates can be related to the voltage \(V\) between the plates and separation \(d\) of the plates by \(E = V/d\text{.}\) Let one of the plates be at \(z=0\) and the other plate at \(z=d\text{,}\) then the \(z\)-component of the electric field will be

\begin{equation*} E_z (t) = \dfrac{V(t)}{d}. \end{equation*}

Now, if we write \(V(t)\) as \(V_0\:\cos(\omega t)\) we get

\begin{equation*} E_z (t) = \dfrac{V_0}{d}\:\cos(\omega t). \end{equation*}

Therefore, the \(z\)-component of the displacement current will be

\begin{equation*} J_{dz} = -\epsilon_0\dfrac{\omega V_0}{d}\:\sin(\omega t). \end{equation*}

Putting in the numerical values we obtain

\begin{align*} \dfrac{\omega V_0}{d} \amp = 8.85\times 10^{-12}\:\dfrac{\text{C}^2}{\text{N.m}^2}\dfrac{150\:\text{s}^{-1}\times 0.015\:\text{v}}{0.002\:\text{m}}\\ \amp = 9.96\:\dfrac{\text{nA}}{\text{m}^2}. \end{align*}

Therefore, the current density is

\begin{equation*} \vec J_d = -\hat k \: \left(9.96\:\dfrac{\text{nA}}{\text{m}^2}\right)\: \sin(150\: t). \end{equation*}

Since the \(x\)- and \(y\)-components of the displacement current density are zero the magnitude of the displacement current is given by the absolute value of the \(z\)-component. \(J_d = |J_{dz}|\text{.}\)

(b) The area of cross-section through which the electric field lines cross between the plates is the area of the plates. Therefore, the total displacement current will be obtained by multiplying \(J_d\) by the area of the plates. This gives

\begin{equation*} I_d = J_d A = \left( 7.97\times 10^{-10}\: \text{A}\right) \: \sin(150\ t). \end{equation*}

Exercises Exercises

1. Displacement Current from a Quadratically Varying Voltage Across Capacitor Plates.

The voltage across a parallel plate capacitor with area \(A\) and separation \(d\) varies with time \(t\) as \(V = a\: t^2\text{,}\) where \(a\) is a constant. (a) Find displacement current density between the plates. (b) Find displacement current between the plates.

Hint.

Answer.

(a) \(2 \epsilon_0\, a t /d\text{,}\) (b) \(\dfrac{2\epsilon_0\omega a A}{d}\: t\text{.}\)

Solution.

(a) Following the arguments presented in Example 42.4 we get

\begin{equation*} E(t) = \dfrac{at^2}{d}. \end{equation*}

Therefore,

\begin{align*} J_d \amp =\epsilon_0\dfrac{\partial}{\partial t} = \epsilon_0\,\dfrac{2at}{d}. \end{align*}

(b) The displacement current \(I_d\) will be

\begin{equation*} I_d = J_d A = \dfrac{2\epsilon_0 a A}{d}\: t. \end{equation*}

2. Displacement Current Density in a Region of Space Where Electric Field is Varying with Time.

In a region of space electric field is pointed along \(y\) axis and varies as a function of \(x\) and \(t\text{.}\)

\begin{equation*} \vec E = \hat j\, (10\ \text{N/C})\cos(20\: x - 500\: t). \end{equation*}

where \(t\) is in nano-sec(ns) and \(x\) in \(\text{cm}\text{.}\)

(a) Find displacement current density vector.

(b) Find the displacement current through a circle of radius \(10\text{ cm}\) centered at the origin in the \(xy\) plane.

(c) Find the displacement current through a circle of radius \(10\text{ cm}\) centered at the origin in the \(yz\) plane.

(d) Find the displacement current through a circle of radius \(10\text{ cm}\) centered at the origin in the \(xz\) plane.

Hint.

(a) Use definitions, (b), (c), (d) Be mindful of directions since \(I = \vec J \cdot \vec A \text{.}\)

Answer.

(a) \(\hat j\ 4.43 \times 10^{-8}\text{ A/m}^2 \sin(20\: x - 500\: t)\text{,}\) (b) 0, (c) \(- 1.4\times 10^{-9}\text{ A } \sin( 500\: t)\text{,}\) (d) 0.

Solution.

(a) From the definition of displacement current density we get \(J_y\) to be

\begin{align*} J_y \amp = \epsilon_0 \dfrac{\partial E_y}{\partial t},\\ \amp = \epsilon_0 \times 10 \times 500 \sin(20\: x - 500\: t),\\ \amp = 4.43 \times 10^{-8}\text{ A/m}^2 \sin(20\: x - 500\: t), \end{align*}

and the other components of \(\vec J\) are zero.

(b) Since normal to the area is \(90^{\circ}\) to the direction of \(\vec J\text{,}\) current through this area is zero.

\begin{align*} I_d \amp = \int_\text{area} J_y dydz = \pi R^2 \times J_y(\text{ at }x=0)\\ \amp =\pi \times 0.1^2\times 4.43 \times 10^{-8}\text{ A/m}^2 \sin( - 500\: t)\\ \amp = - 1.4\times 10^{-9}\text{ A } \sin( 500\: t) \end{align*}

(d) Since normal to the area is \(90^{\circ}\) to the direction of \(\vec J\text{,}\) current through this area is zero.

Prev Top Next