Chapter 10 Rigid Body Motion
In the last chapter we studied rotation about a fixed axis. Although, rotation about a fixed axis covers a lot of common applications, there are important applications, such as gyroscope, rotation of planets, tumbling bodies, etc, where axis of rotation, itself rotates. In this chapter we will tackle some of these problems.
Between the general rotation and fixed-axis rotation is a situation of a fixed-point rotation, where rather than a full axis remaining fixed, we require that one point remaining fixed which will allow for study of precession of axis of rotation.
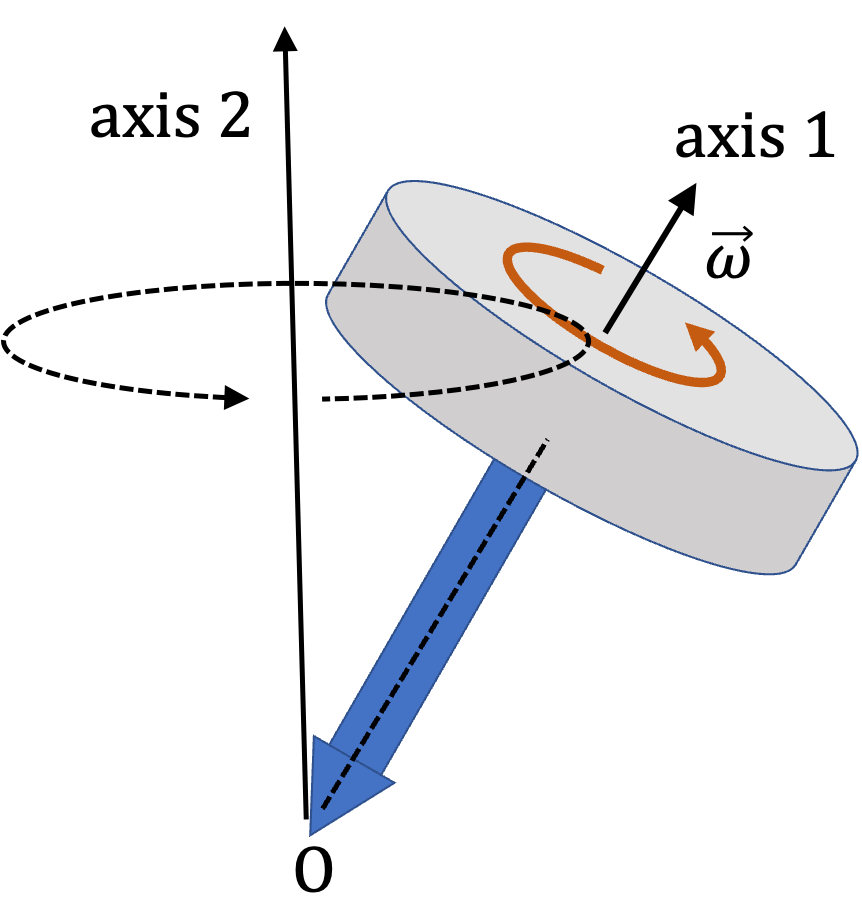
Figure 10.1 shows an example of a fixed-point rotation. While the top is spinning (i.e., pure rotation) about axis 1, this axis of rotation itself rotates about another axis, axis 2, with one point O fixed. The motion of angular velocity vector \(\vec \omega\) about axis 2 is called precession.
Unlike the fixed-axis rotation, where you could take care of vector nature of angular quantities by just following the “sense of rotation”, here you will need to treat vectors more analytically. We will start by first a review of angular velocity \(\vec \omega\text{,}\) angular momentum \(\vec L\) and torque \(\vec {\mathcal{T}}\text{.}\)

