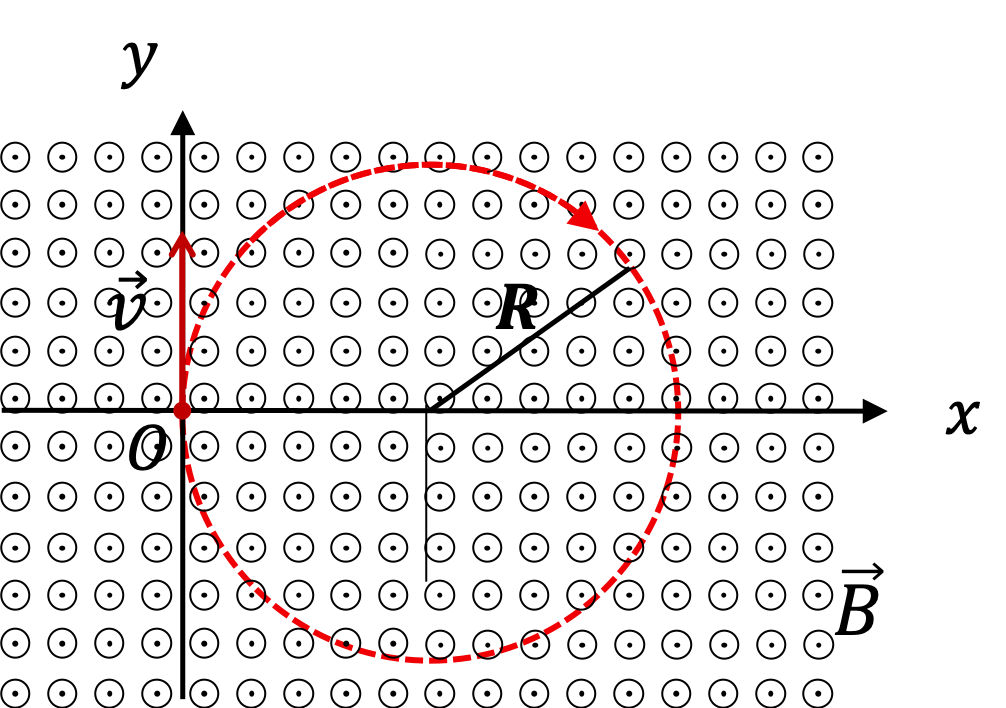
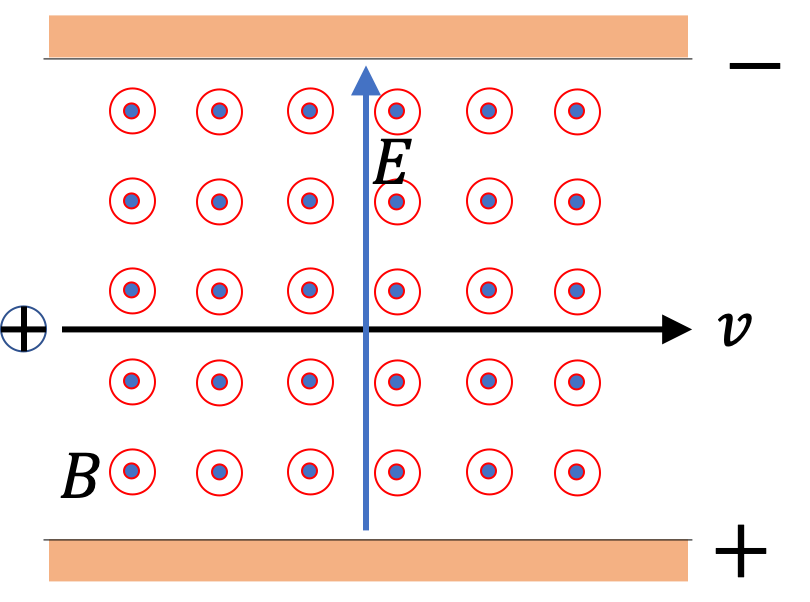
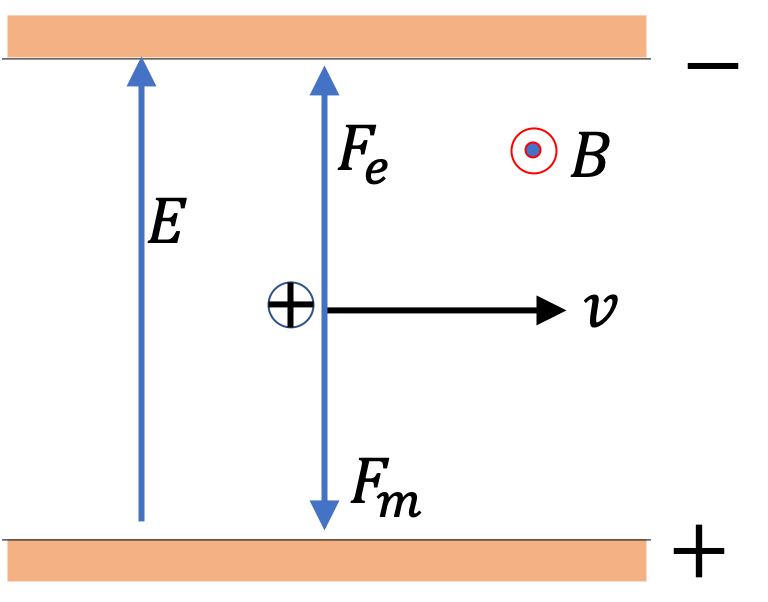
Consider a particle of mass \(m\) and charge Q moving in a uniform magnetic field of magnitude \(B_0\text{,}\) which is pointed towards positive \(z\) axis. We assume only magnetic forces on the particle are relevant. Then, equation of motion of the particle,
\begin{equation*}
m\dfrac{d\vec v}{dt} = Q\vec v \times \vec B,
\end{equation*}
takes the following component form.
\begin{align*}
\dfrac{dv_x}{dt} \amp = \dfrac{QB_0}{m}\,v_y, \\
\dfrac{dv_y}{dt} \amp = -\dfrac{QB_0}{m}\,v_x, \\
\frac{dv_z}{dt} \amp = 0.
\end{align*}
Denote \(Q B_0/m\) by symbol \(\Omega\) to simplify writing.
\begin{equation*}
\Omega = \dfrac{QB_0}{m}.
\end{equation*}
Therefore, the equations of motion are
\begin{align}
\dfrac{dv_x}{dt} \amp = \Omega\,v_y, \tag{35.11}\\
\dfrac{dv_y}{dt} \amp = -\Omega\,v_x, \tag{35.12}\\
\frac{dv_z}{dt} \amp = 0. \tag{35.13}
\end{align}
We wish to solve this equation for given initial velocity, \(\vec v_0 = \left( v_{0x},\ v_{0y}\ v_{0z}\right)\text{.}\) First notice that we can get separate equations for v_x and v_y.
\begin{align}
\dfrac{d^2v_x}{dt^2} \amp = -\Omega^2\,v_x, \tag{35.14}\\
\dfrac{d^2v_y}{dt^2} \amp = -\Omega^2\,v_y, \tag{35.15}\\
\frac{dv_z}{dt} \amp = 0. \tag{35.16}
\end{align}
The solutions are
\begin{align*}
\amp v_x(t) = A \cos(\Omega t) + B \sin(\Omega t), \\
\amp v_y(t) = C \cos(\Omega t) + D \sin(\Omega t), \\
\amp v_z(t) = E,
\end{align*}
where \(A,\ B,\ C,\ D,\ E\) are constants. By using the initial veocity condition, we get
\begin{equation*}
E = v_{0z},
\end{equation*}
Note\(A,\ B,\ C,\ D\) are not all independent since derivative of \(v_x\) is proportional to \(v_y\text{.}\) Therefore, we must have
\begin{equation*}
-\Omega A \sin(\Omega t) + \Omega B \cos(\Omega t) =\Omega C \cos(\Omega t) + \Omega D \sin(\Omega t).
\end{equation*}
Therefore,
\begin{equation*}
-A = D,\ \ B = C.
\end{equation*}
Therefore, we write \(v_x \) and \(v_y\) with only two constants.
\begin{align*}
\amp v_x(t) = A \cos(\Omega t) + B \sin(\Omega t), \\
\amp v_y(t) = B \cos(\Omega t) - A \sin(\Omega t),
\end{align*}
Now, we use initial conditions on these components.
\begin{align*}
\amp v_{0x} = A, \\
\amp v_{0y} = B,
\end{align*}
Finally, we have velocity at arbitray time
\begin{align*}
\amp v_x(t) = v_{0x} \cos(\Omega t) + v_{0y} \sin(\Omega t), \\
\amp v_y(t) = v_{0y} \cos(\Omega t) - v_{0x} \sin(\Omega t), \\
\amp v_z(t) = v_{0z}.
\end{align*}
From these we can obtain position of the particle at arbitrary instant by simply integrating. Let position at initial instant be \(\vec r_0 = (0,\ 0,\ 0)\text{.}\)
\begin{align*}
\amp x(t) = \dfrac{v_{0x}}{\Omega} \sin(\Omega t) + \dfrac{v_{0y}}{\Omega} \left(1- \cos(\Omega t) \right), \\
\amp y(t) = \dfrac{v_{0y}}{\Omega} \sin(\Omega t) - \dfrac{v_{0x}}{\Omega} \left( 1 - \cos(\Omega t) \right), \\
\amp z(t) = v_{0z} t.
\end{align*}