Skip to main content
   
Logo image

Physics Bootcamp

Samuel J. Ling

Section 31.6 Electric Potential of Charge Distributions

A charged object, such as a plastic rod rubbed with a rabbit fur, usually has a large number of charges. To handle thess types of situations, we model them with a continuous charge density. Then, we divide the charge distribution into small cells and replace charges in cells by point charges at their locations, to which we apply methods of discrete charges we learned in Section 31.4.
To be specific about the method for handling continuous charges, let us consider finding electric potential at point P by a charge distribution of an arbitrary shape shown in Figure 31.20.
Figure 31.20.
Let \(\rho\) represent the charge density. As per our plan we divide up the charged body into cells. Let \(q_i\) denote the charge in cell at coordinate \((x_i, y_i, z_i)\text{.}\) Let \(\Delta V_i\) denote the volume of this cell. Then,
\begin{equation*} q_i = \rho \Delta V_i. \end{equation*}
This discretization results in a finite number of charges located at the cells of the body. Let \(N\) be the total number of these cells. In Section 31.4 we found that potential for \(N\) charges is given by
\begin{equation} \phi_P = \dfrac{1}{4\pi\epsilon_0}\, \sum_{i=1}^{N} \dfrac{ q_i}{r_i} = \dfrac{1}{4\pi\epsilon_0}\, \sum_{i=1}^{N} \dfrac{ \rho\Delta V_i}{r_i}, \tag{31.15} \end{equation}
where \(r_i \) is distance from charge \(q_i \) to the field point P. Using Cartesian coordinates \((x_i,\ y_i,\ z_i)\) of charge \(q_i\) and field point P \((x,\ y,\ z)\) these distances are
\begin{equation*} r_i = \sqrt{ (x-x_i)^2 + (y-y_i)^2 + (z-z_i)^2 }. \end{equation*}

Subsection 31.6.1 (Calculus) Electric Potential of a Charge Distribution

In the limit of infinitesimal cells in Eq. (31.15), the sum becomes an integral, which we can formally write the result as a coneptual integral.
\begin{equation} \phi_P = \frac{1}{4\pi\epsilon_0}\int_{\text{cells}}\frac{dq}{r_{\text{cell-to-P}}},\tag{31.16} \end{equation}
where \(r_{\text{cell-to-P}}\) is the distance to point P from the infinitesimal cell. Note that this is just a concetual integral - in each situation, you will use this equation as a guide and discover the actual integral that you can evaluate to get your answer.
To be concrete, let the position of the space point P be denoted as \(\vec r\) and the position of a representative cell element be \(\vec r^{\prime}\text{,}\) then the integral can be written more explicitly.
\begin{equation} \phi_P = \frac{1}{4\pi\epsilon_0}\int_{\text{cells}}\frac{dq}{|\vec r-\vec r^{\prime}|},\tag{31.17} \end{equation}
where \(dq\) refers to the charge in the cell at position \(\vec r^{\prime}\text{.}\)
As we have seen before that charge distribution the formula for elemental charge \(dq\) depends on the dimensions over which the charges are distributed. Thus, in one-, two-, and three-dimensional situations, we use different symbols for charge densities and volume elements.
\begin{equation} dq = \begin{cases} \lambda dl \amp (1-\text{dim})\\ \sigma dA \amp (2-\text{dim})\\ \rho dV \amp (3-\text{dim}) \end{cases}\tag{31.18} \end{equation}
Here \(\lambda\) is charge per unit length, \(\sigma\) charge per unit area and \(\rho\) charge per unit volume. In order to reduce algebra, it is often helpful to pick the shape of the cell in accordance with the geometry of the charge distribution and exploit any symmetry in the problem. The following examples illustrate calculations for electrical potential of continuous charge distributions.

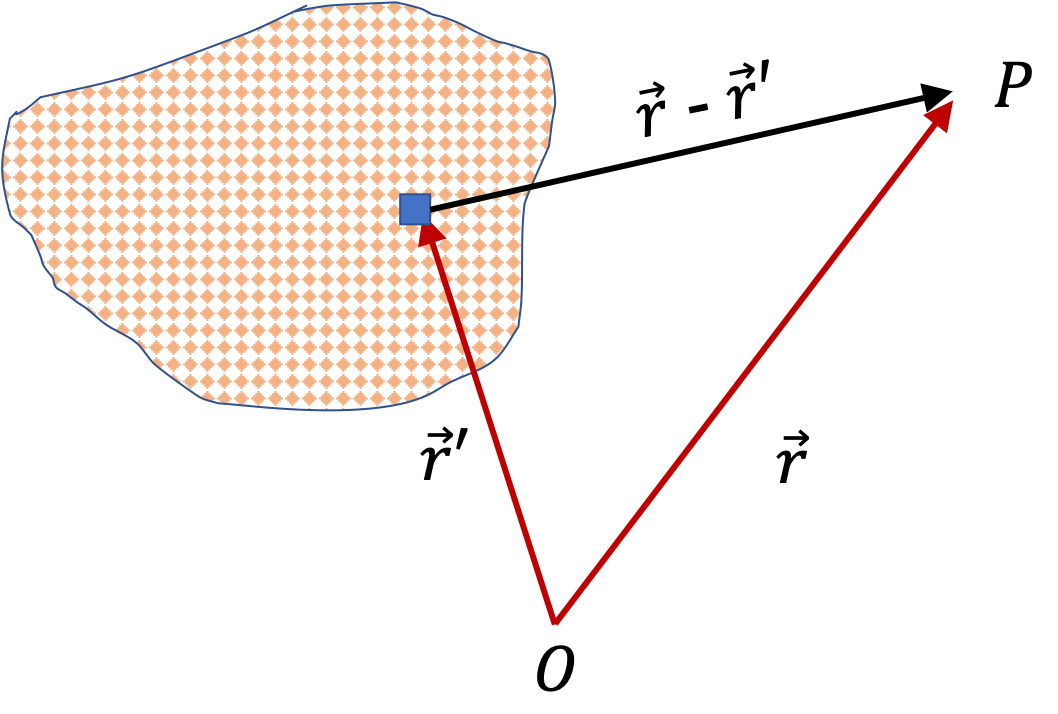
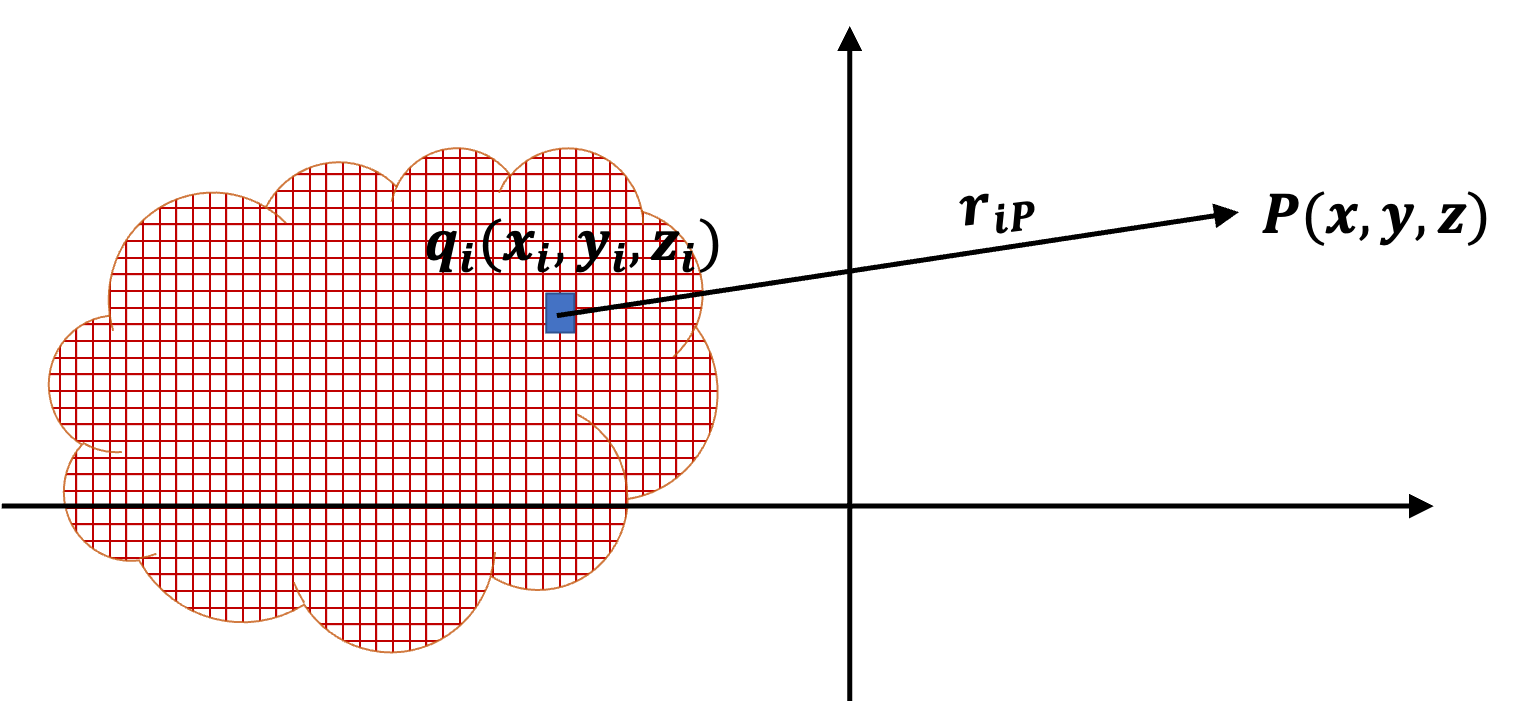Example 31.21. (Calculus) Electric Potential of a Uniform Line of Charge.

Find the electric potential of a uniformly charged non-conducting wire with linear density \(\lambda\) (SI units \(\text{C/m} \)) and length \(L\) at a point that lies on a line that divides the wire into two equal parts.
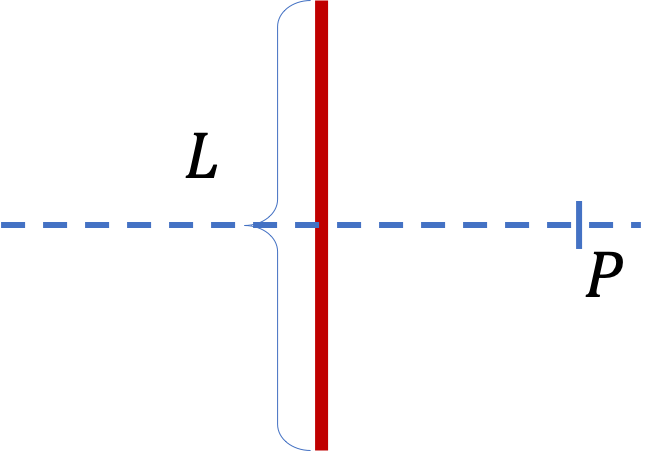
Answer.
\(\dfrac{\lambda}{4\pi\epsilon_0}\, \ln\left( \dfrac{\sqrt{x^2 + (L/2)^2} + L/2}{ \sqrt{x^2 + (L/2)^2} - L/2 } \right)\text{.}\)
Solution.
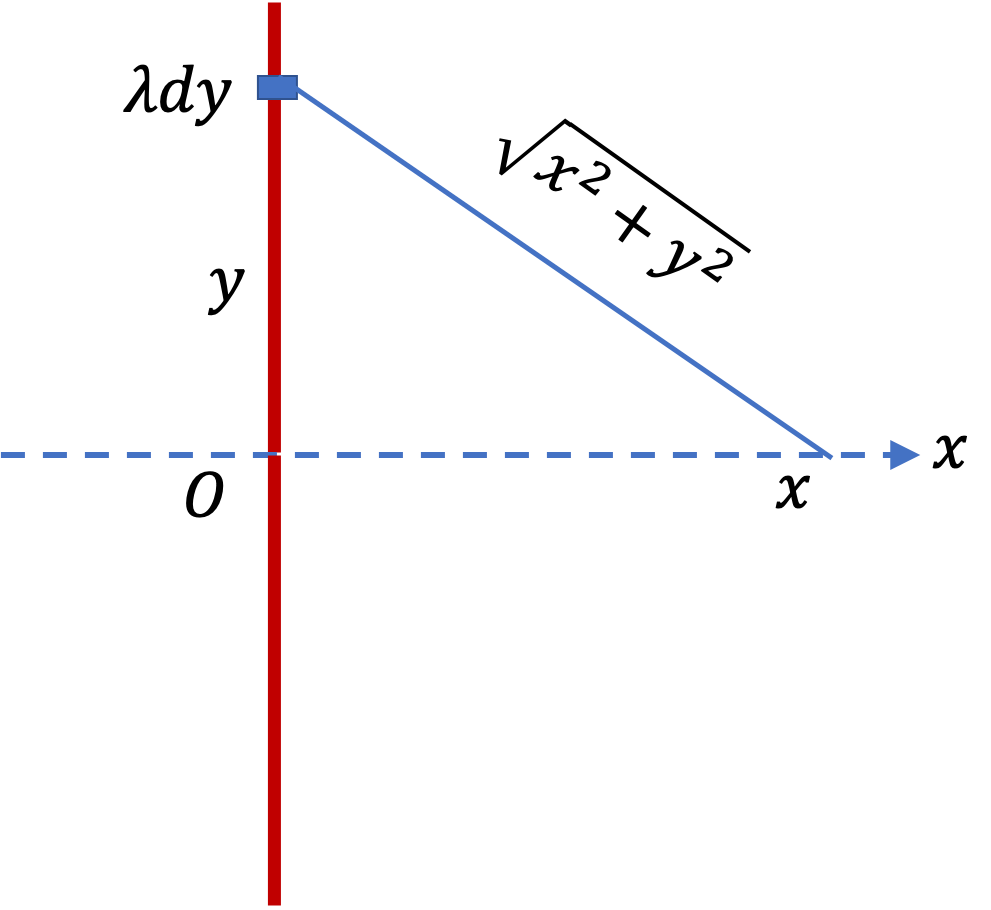
We start with identifying a representative cell on the line. This is shown in the figure as an infinitesimal elment at coordinate \(y\text{.}\) The charge in the cell is \(dq = \lambda\,dy\text{.}\) From the figure, it is clear that the electric potential of this charge will be
\begin{equation*} d\phi = \dfrac{1}{4\pi\epsilon_0}\, \dfrac{\lambda\, dy}{\sqrt{x^2 + y^2}}. \end{equation*}
Here \(x\) is the field point. Therefore, when we sum over (i.e. integrate) the charges, we will keep \(x\) fixed. We will get the net potential at \((x,0)\text{,}\) which is the location of the field point.
Carrying out the integration yields the answer.
\begin{align*} \phi_P \amp = \dfrac{\lambda}{4\pi\epsilon_0}\, \int_{-L/2}^{L/2} \dfrac{dy}{\sqrt{x^2 + y^2}} \\ \amp = \dfrac{\lambda}{4\pi\epsilon_0}\, \ln\left( \dfrac{\sqrt{x^2 + (L/2)^2} + L/2}{ \sqrt{x^2 + (L/2)^2} - L/2 } \right). \end{align*}

Example 31.22. Electric Potential of a Uniformly Charged ring.

A ring of radius \(R\) has a uniform charge density \(\lambda\) (SI units \(\text{C/m}\) ) as shown in Figure 31.23. Find the electric potential at a point on the axis of the ring a distance \(h\) above the center.
Figure 31.23.
Answer.
\(\dfrac{1}{4\pi\epsilon_0}\, \dfrac{2\pi R \lambda}{\sqrt{R^2 + h^2} }\text{.}\)
Solution.
Every charge of the ring has the same distance to the field point.
\begin{equation*} r = \sqrt{R^2 + h^2}. \end{equation*}
Therefore, each charge will have the same potential there. Hence, we will get
\begin{align*} \phi_P\amp = \dfrac{1}{4\pi\epsilon_0}\, \dfrac{q_\text{tot}}{r}\\ \amp = \dfrac{1}{4\pi\epsilon_0}\, \dfrac{2\pi R \lambda}{\sqrt{R^2 + h^2} }. \end{align*}

Example 31.24. (Calculus) Electric Potential of a Uniformly Charged Disk.

(a) Find the electric potential of a uniformly charged nonconducting disk of radius \(R\) with charge density \(\sigma \) (\(\text{C/m}^2\)) at a point on the axis as shown in Figure 31.25. For concrteteness, let the field point on the axis be at a height \(h\) from the center of the disk.
Figure 31.25.
(b) Take \(h/R\rightarrow 0\) on your answer to show that very near the disk, potential varies as linearly with \(h\text{.}\) You should get \((\sigma/2\epsilon_0)(R-h)\) in the leading order in \(h/R\text{.}\)
(c) Take \(R/h\rightarrow 0\) on your answer to show that very far away from the disk, potential at height \(h\) is that of a point charge equal to total charge on the disk.
Answer.
(a) \(\frac{\sigma }{2\epsilon_0}\left( \sqrt{h^2 + R^2} -h\right)\text{.}\)
Solution 1. (a)
(a) We will discretize the disk in the shape of rings of thickness \(dr\text{.}\) One such ring of radius \(r\) is shown in Figure 31.26. The potential from charges in this infintesimal ring can easily be seen to be
\begin{equation*} d\phi = \frac{1}{4\pi\epsilon_0}\,\frac{dq}{\sqrt{h^2 + r^2}}, \end{equation*}
where \(dq = \sigma \times 2\pi r dr\text{.}\)
Figure 31.26.
Integrating from \(r=0\) to \(r=R\) will give us the answer.
\begin{align*} \phi \amp = \frac{1}{4\pi\epsilon_0}\int_0^R \frac{2\pi\sigma r dr}{\sqrt{h^2 + r^2}}\\ \amp = \frac{\sigma }{2\epsilon_0}\int_0^R \frac{r dr}{\sqrt{h^2 + r^2}}\\ \amp = \frac{\sigma }{2\epsilon_0}\left( \sqrt{h^2 + R^2} -h\right) \end{align*}
Solution 2. (b)
(b) To take \(h/R\rightarrow 0\) limit, let us factor out \(R\) to get
\begin{equation*} \frac{\sigma R}{2\epsilon_0}\left( \sqrt{ 1 + (h/R)^2} -h/R\right). \end{equation*}
Let us denote \(h/R = x\) and then expand \(\sqrt{1+x^2}\approx 1 + \frac{1}{2}x^2\) to get
\begin{equation*} \frac{\sigma R}{2\epsilon_0}\left( 1 + \frac{1}{2}x^2 - x \right). \end{equation*}
Now, noting that when \(x\) gets small \(x \gg x^2\text{.}\) therefore, we drop the quadratic term, but keep the linear term -- since dropping that will get rid of information about \(h\)-dependence altogether. Restoring \(h/R\text{,}\) we get
\begin{equation*} \frac{\sigma}{2\epsilon_0}\left( R - h \right). \end{equation*}
Solution 3. (c)
(c) Here we want to take \(R/h\rightarrow 0\text{.}\) Therefore, we factor out \(h\text{.}\)
\begin{equation*} \frac{\sigma h}{2\epsilon_0}\left( \sqrt{ 1 + (R/h)^2} -1\right). \end{equation*}
Let \(x=R/h\) and expand the square root. Keep upto the leading terms that has \(h\) in it, we get
\begin{equation*} \frac{\sigma h}{2\epsilon_0}\frac{1}{2} \frac{R^2}{h^2}. \end{equation*}
Noting that total charge is \(q_\text{tot}=2\pi R^2\sigma\text{,}\) this is
\begin{equation*} \frac{1}{4\pi\epsilon_0}\frac{q_\text{tot}}{h}. \end{equation*}
That is, far away from the disk, the potential is that of a point charge eaual to total charge placed at the center.
PrevTopNext
Found typo?