Coupled Motion and Constraints

Section 6.17 Coupled Motion and Constraints

When motion of two or more bodies are connected, we say that their motion is coupled. One way to analytically see the relation among the motion is look at the displacement of various bodies in some interval \(\Delta t\text{.}\) Sometimes, you can see this in the relation between their coordinates and other times you will have to look at two times \(t\) and \(t+\Delta t\text{.}\) These relations are called constraints.

Analytically, we think of individual parts of a coupled system as separate systems that are linked by one or more constraints. The equations of each together with the constraints are then analyzed to gain insight into the motion of the original system. In this section, we will look at two common types of problems that you often see in introductory books.

Subsection 6.17.1 Objects Pushing on Each Other

Place one book next to another. Now, push on one of the books towards the other book as in Figure 6.84. Notice how the two books move together. We say that the displacements of the two books are “coupled”.

Figure 6.84. Two books move together when pushed by force \(F\) with constraint \(x_2 - x_1 = D\text{,}\) a constant.

For example, in the example of the two books in Figure 6.84, say their motion is along \(x\) axis. Let positions of the two books be denoted by symbols, \(x_1 \) and \(x_2\text{.}\) We can express the constraint here either by saying the the difference of these coordinates is a fixed quantity, say \(D \text{,}\)

\begin{equation} x_2 - x_1 = D.\tag{6.34} \end{equation}

or, that any change in \(x_1 \) must equal the change in \(x_2 \text{.}\)

\begin{equation*} \Delta x_1 = \Delta x_2. \end{equation*}

This leads to their velocities and accelerations also equal.

\begin{equation*} v_{1,x} = v_{2,x},\ \ \text{and}\ \ a_{1,x} = a_{2,x}. \end{equation*}

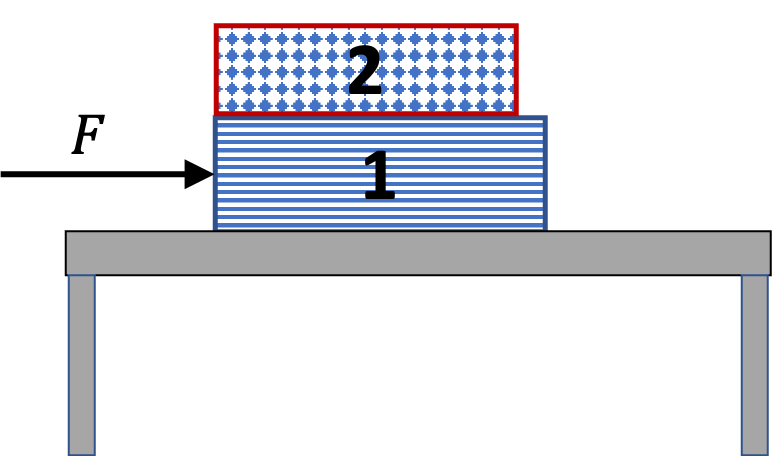
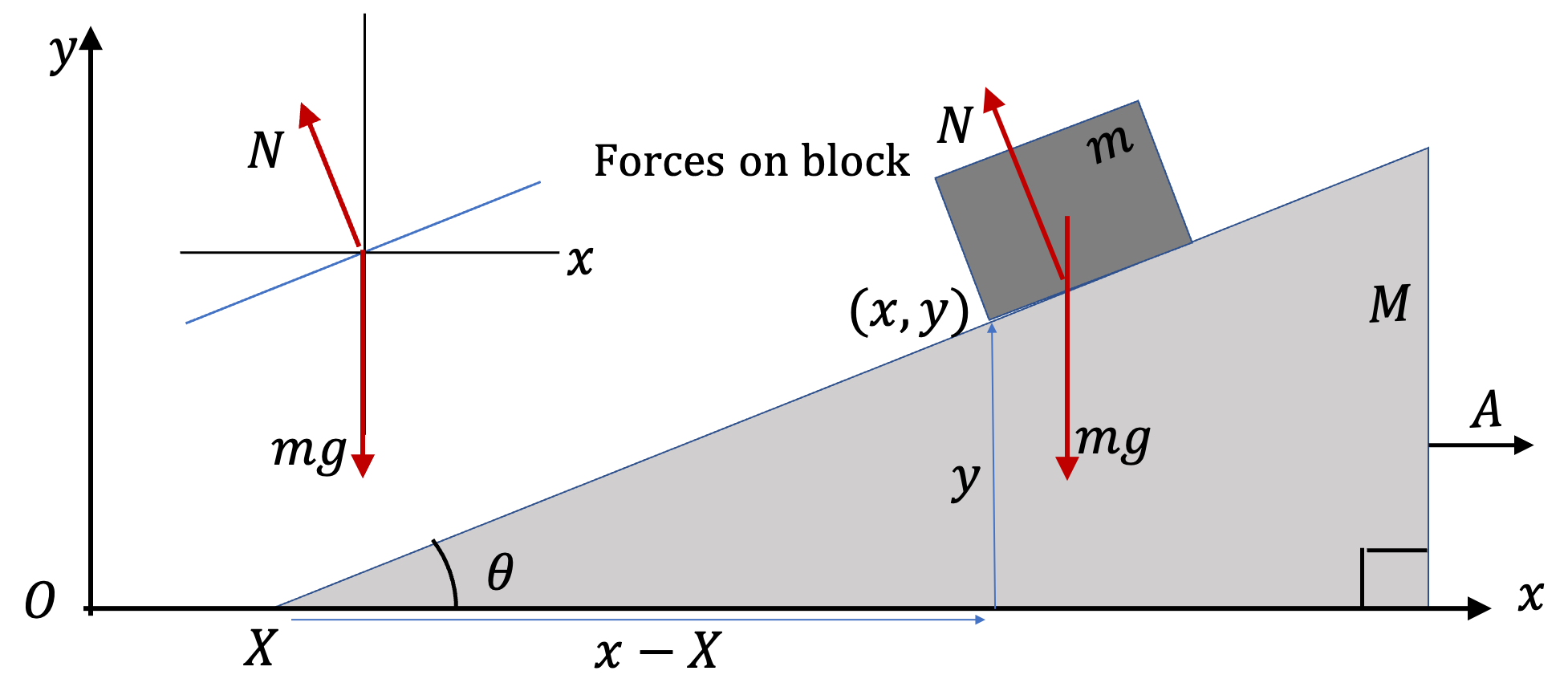
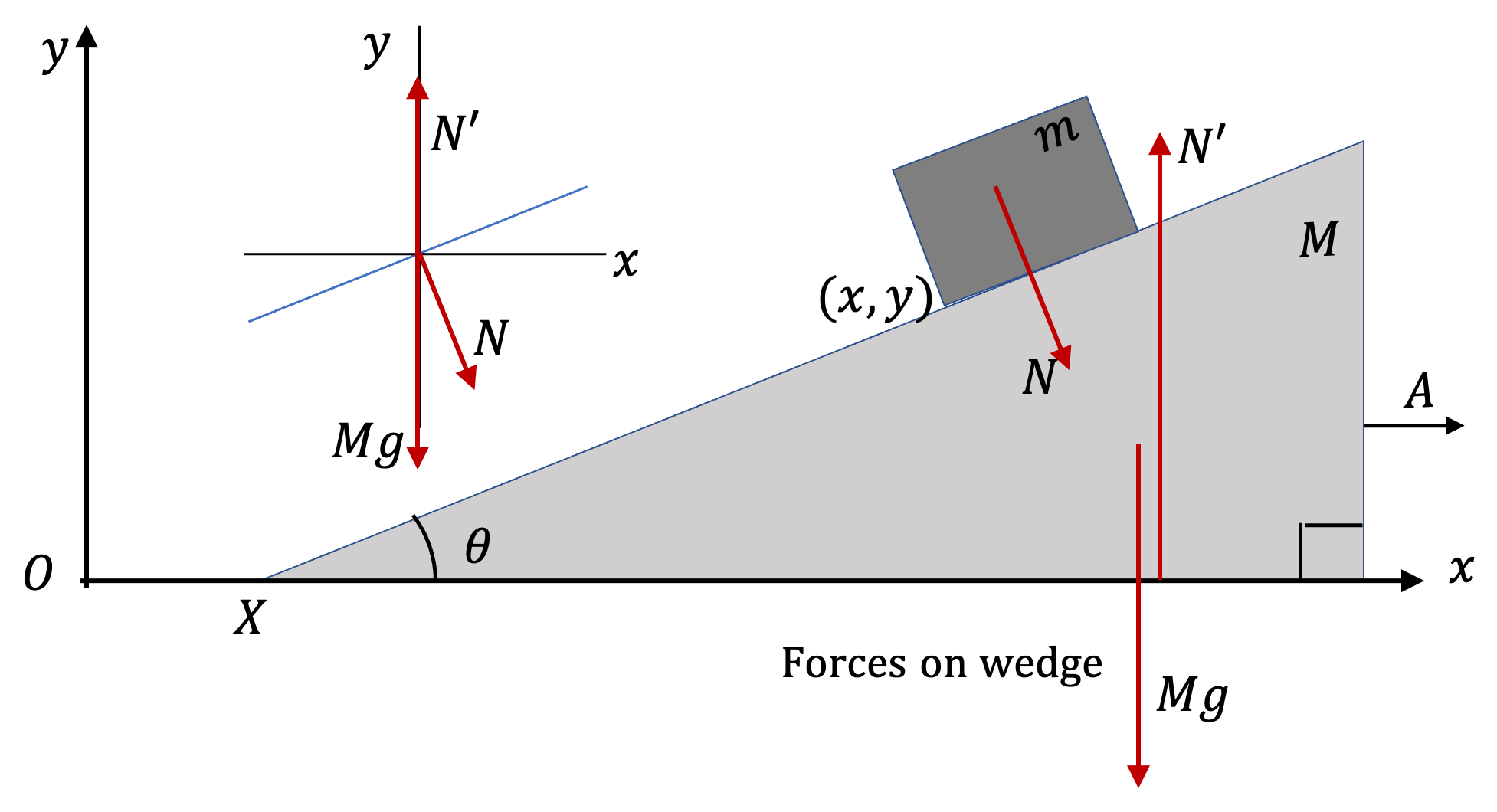
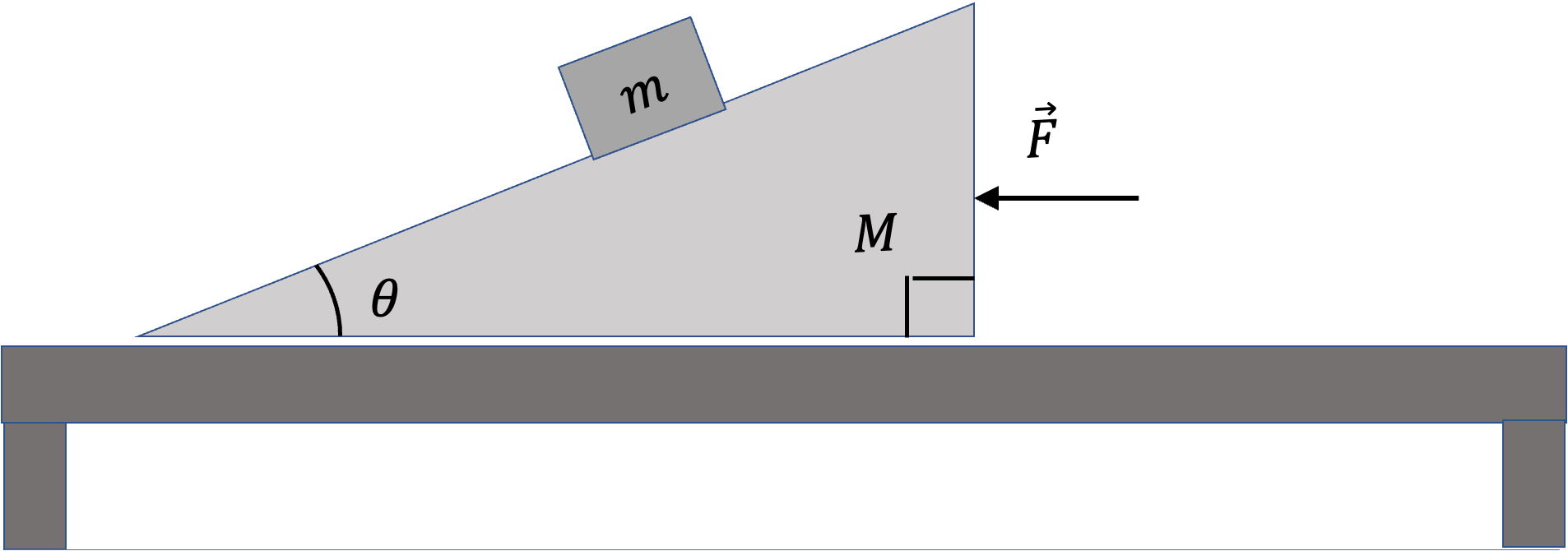
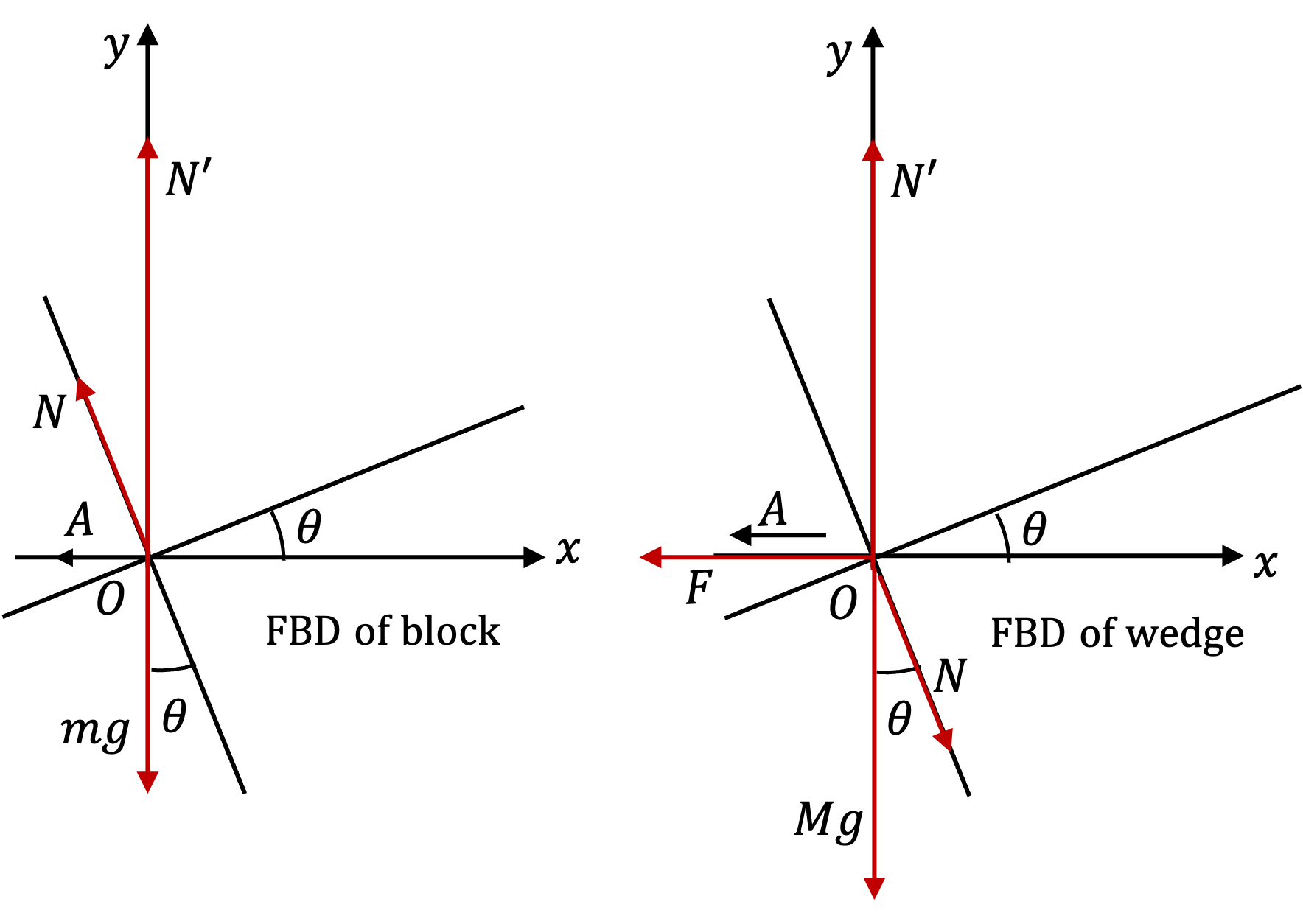
Example 6.85. Force between Two Books Moving Together.

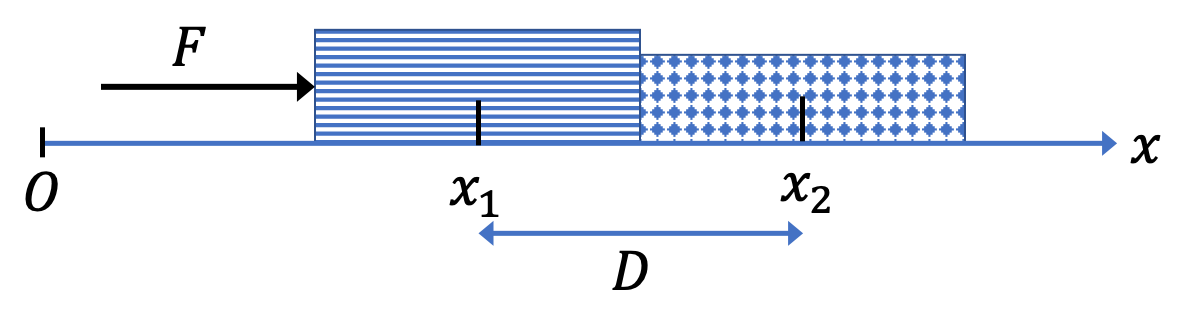
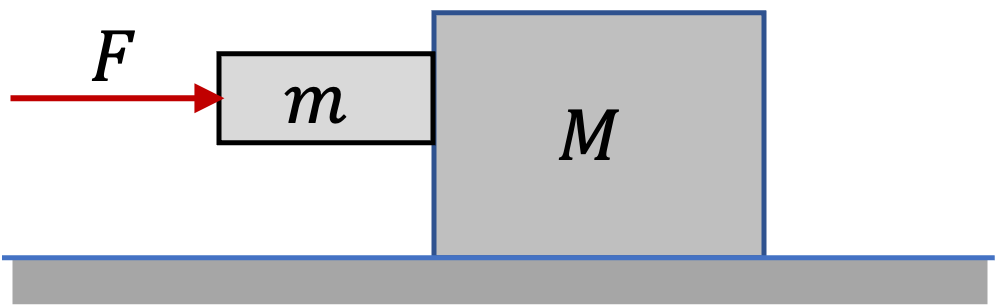
Consider two books of masses \(m_1\) and \(m_2\) that are next to each other on a frictionless table as shown in Figure 6.86. A constant force \(\vec F\) pushes on book 1 horizontally.

(a) What is the magnitude of the acceleration of the two books?

(b) What is the magnitude and direction of the force on book 1 by book 2?

Answer.

(a) \(\dfrac{F}{m_1 + m_2}\text{,}\) (b) magnitude = \(\dfrac{m_1}{m_1 + m_2}\, F\text{,}\) direction opposite to \(\vec F\text{.}\)

Solution 1. a

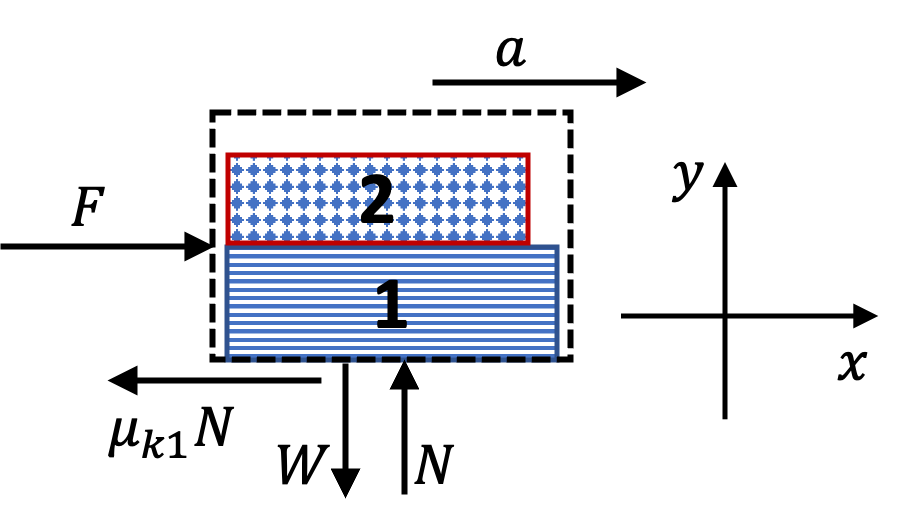
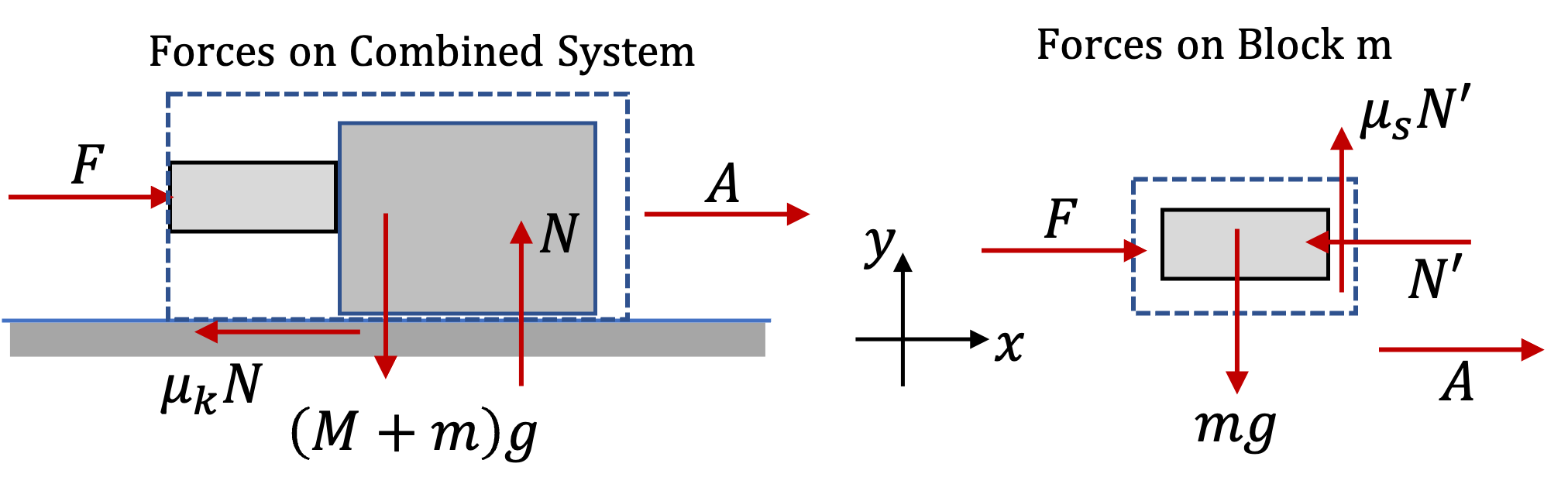
Since we want the acceleration of both, we can look at the two books together as one system and investigate forces on the combined system. The forces are shown in Figure 6.87 along with the choice of Cartesian axes.

Figure 6.87. Figure for Example 6.85(a).

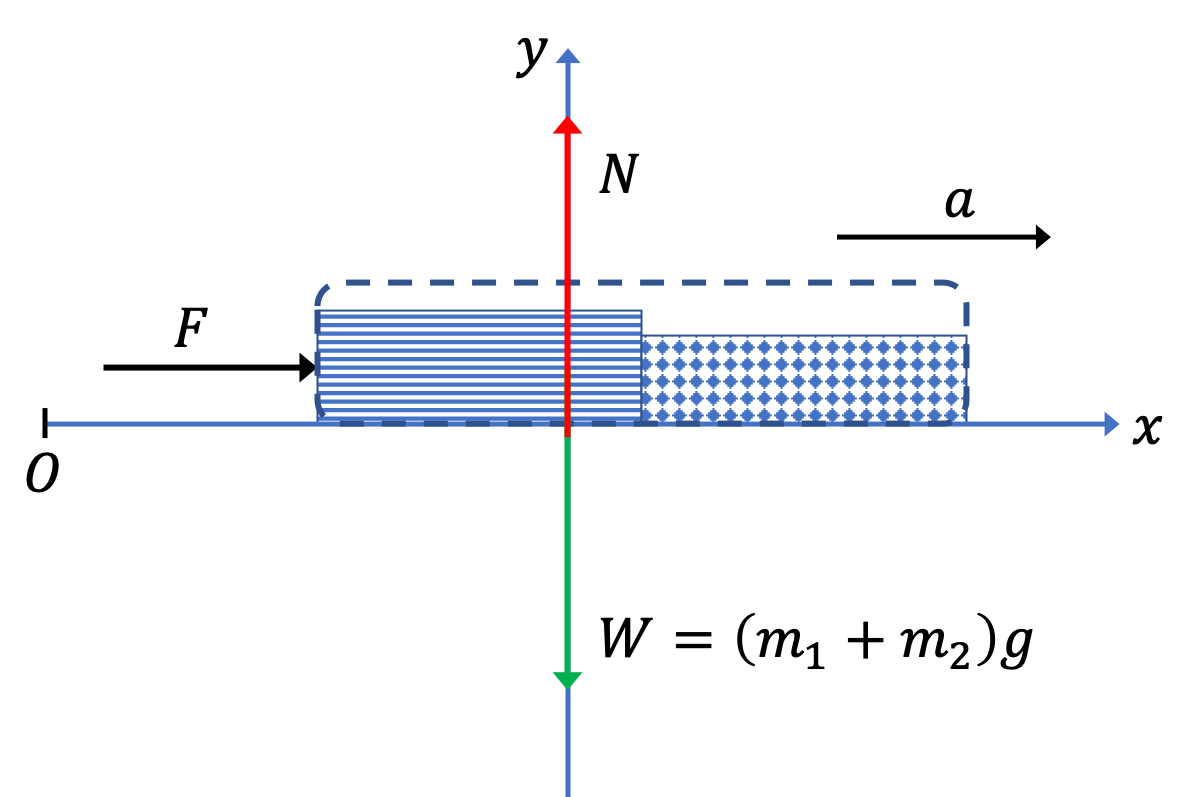
Equations of motion along the two Cartesian axes are

\begin{align*} \amp\text{ Along }x\text{ axis: } F = \left( m_1 + m_2 \right) a,\\ \amp\text{ Along }y\text{ axis: } N - \left( m_1 + m_2 \right) g = 0. \end{align*}

From the first equation, we have our answer.

\begin{equation*} a = \dfrac{F}{m_1 + m_2}. \end{equation*}

Solution 2. b

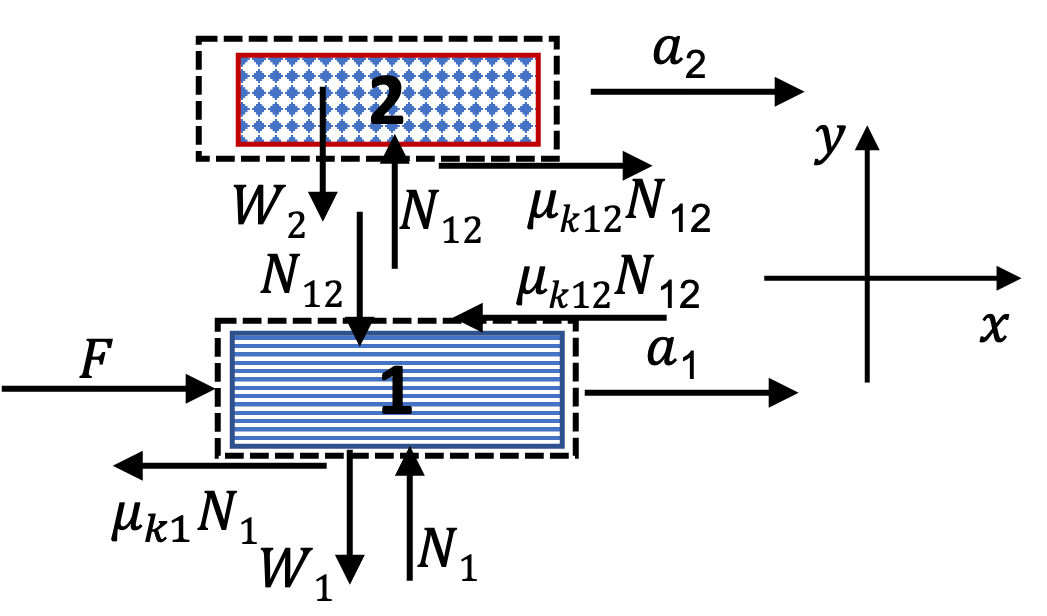
Since we now want force on one of the books by the other book, we will need to set up force diagram of one book. Here, we want the force on book 1. So, it may seem “natural” to look at the force diagram of book 1, but it turns out it is easier to get this information from force diagram on 2 as we will show after I do the first way.

Using force diagram on 1:

Figure 6.88 gives the forces on book 1 alone. Note that we have a new force here, the (normal) force by book 2 on book1.

Figure 6.88. Figure for Example 6.85(b).

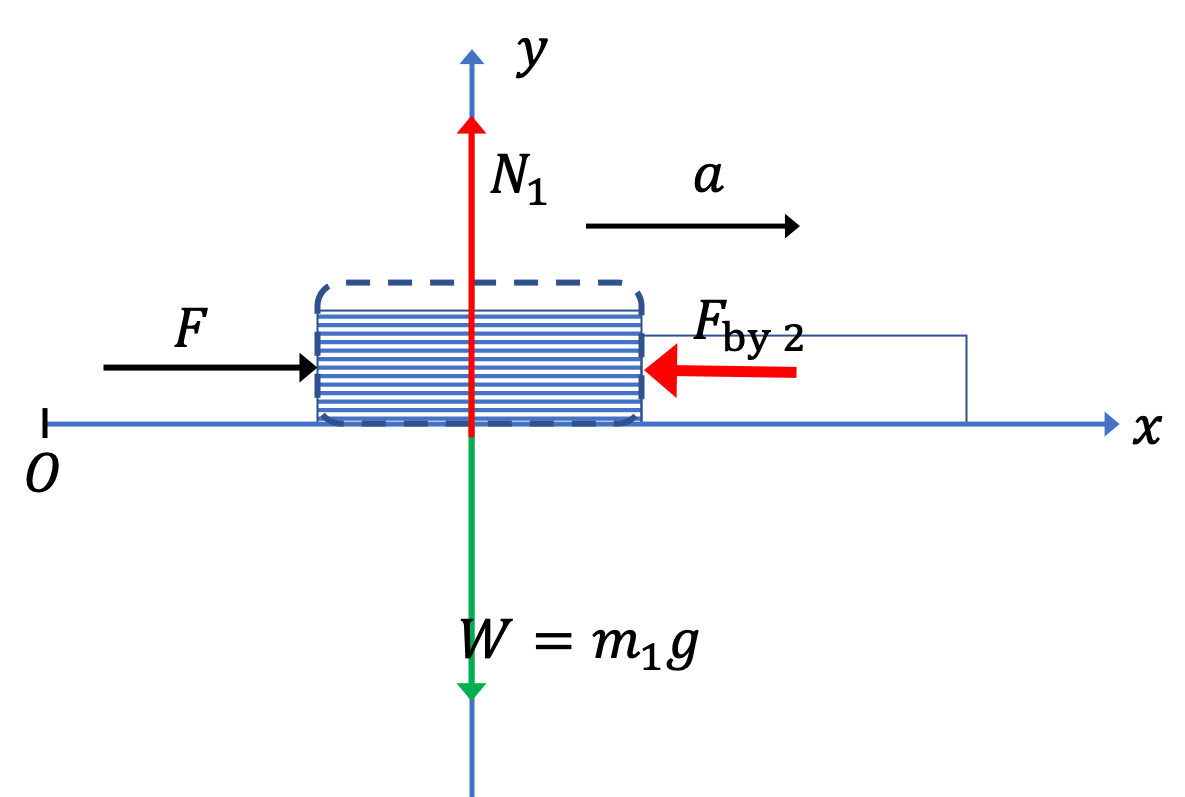
Now, the \(x \) axis equation of motion is

\begin{equation*} F - F_{\text{by 2}}= m_1\, a, \end{equation*}

where we can use the \(a \) we found in part (a) to give

\begin{equation*} F_{\text{by 2}} = F - m_1\,\dfrac{F}{m_1 + m_2} = \dfrac{m_2}{m_1 + m_2}\, F. \end{equation*}

Using force diagram on 2:

Figure 6.89 gives the forces on book 2 along with \(\vec F \text{,}\) which is here for illustrative purposes only. Note that force \(\vec F \) does not act on book 2 - its acting on book 1 or (combined book 1 and book 2, but not on book 2 alone) - since the person pushing book 1 is not in contact with book 2.

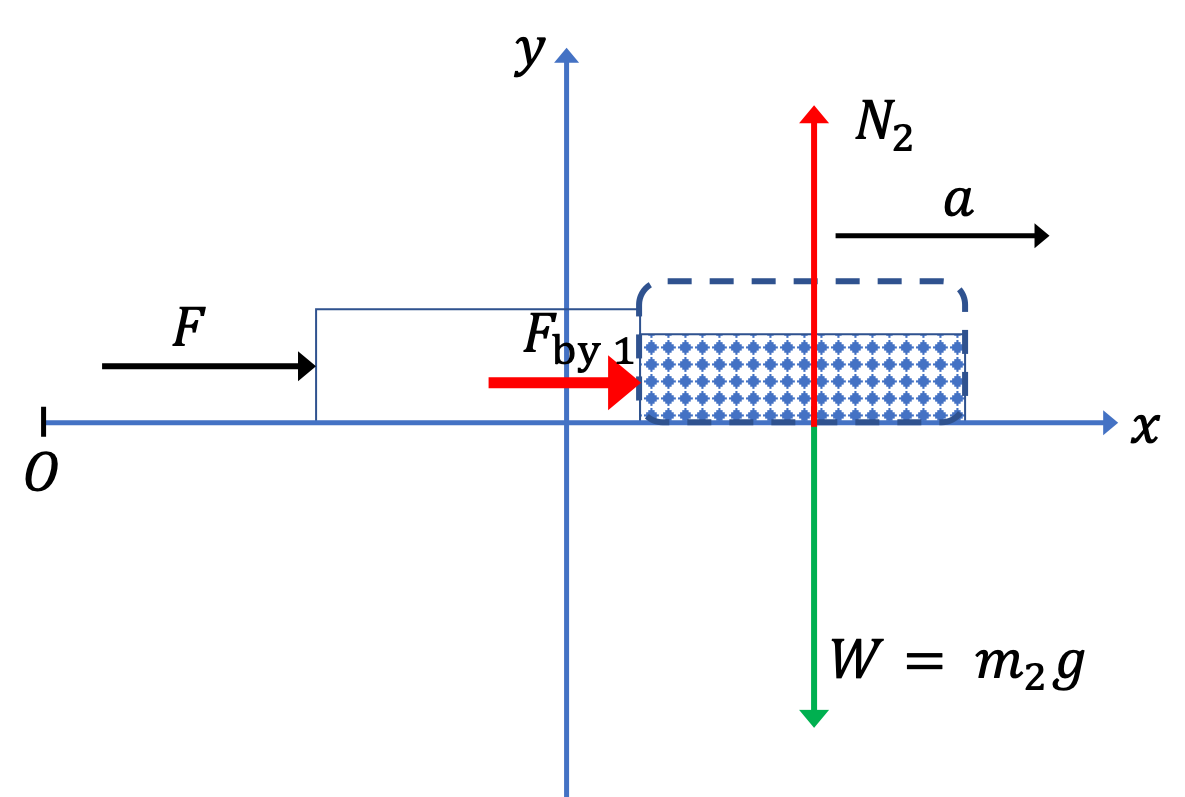
Figure 6.89. Figure for Example 6.85(book2).

Now, the \(x \) axis equation of motion is

\begin{equation*} F_{\text{by 1}}= m_2\, a, \end{equation*}

where we can use the \(a \) we found in part (a) to give

\begin{equation*} F_{\text{on 2}}^\text{by 1} = \dfrac{m_2}{m_1 + m_2}\, F. \end{equation*}

But by third law, this is equal to \(F_{\text{on 1}}^\text{by 2}\text{.}\)

Subsection 6.17.2 Motion Connected by Strings and Pulleys

In a similar way, displacements of two blocks conected by a string around a pulley are linked if the length of the string does not change during their motion - the amount one moves up is equal to the amount the other moves down. Here, we write the constraint as \(h_1 + \pi R + h_2 = \text{constant}\text{,}\) where \(h_1 (h_2)\) is the length of the rope on mass 1(2) side and \(R\) is the radius of the pulley.

In the example of the masses on the pulley, let us point positive \(y \) axis up and let \(y_1 \) and \(y_2\) denote the positions of the two blocks. Then, constraint will be

\begin{equation*} \Delta y_1 = - \Delta y_2. \end{equation*}

Note the crucial negative sign here - as one goes up the other goes down.

This gives the following relations between \(y\)-components of their velocities and accelerations.

\begin{equation*} v_{1,y} = - v_{2,y},\ \ \text{and}\ \ a_{1,y} = -a_{2,y}. \end{equation*}

Furthermore, if we look at the string moving on the edge of the pulley, we can also relate the distances blocks rise or fall to the angle \(\Delta \theta\text{,}\) the pulley rotates if string does not slide on the pulley by using the arc-angle relation, \(s=R\theta\) of a circular arc.

\begin{equation*} R\Delta \theta = |\Delta y_1| = |\Delta y_2|. \end{equation*}

Example 6.91. Two Blocks Moving Vertically Coupled Through an Ideal Pulley.

Two blocks of mass \(m_1 \) and \(m_2 \) are conncted by a string that goes over an ideal pulley. By ideal pulley, we will mean that the tensions on the two sides of the pulley can be assumed to have same magnitude. Both blocks are hanging with initially kept in place by some support force, which is not shown in the figure. Once the support force is removed, the two blocks start to accelerate. This system is called Atwood’s machine.

(a) Find the acceleration of the two blocks.

(b) Find the magnitude of tension in the string.

(c) If block 2 has less mass than block 1, block 2 will rise and block 1 will fall. By how much height would block 2 rise in time \(\Delta t \) starting from rest?

Check your answer for the following values: \(m_1 = 8.0\text{ kg}\text{,}\) \(m_2 = 2.0\text{ kg}\text{,}\) \(\Delta t = 0.75\text{ s}\text{.}\)

Answer.

(a) \(5.89\text{ m/s}^2\text{,}\) (b) \(15.7\text{ N} \text{,}\) (c) \(0.184\text{ m}\text{.}\)

Solution 1. (a) and (b)

We will write equations of motions of the two blocks by working \(\vec F = m\vec a \) for each, with two common values, the magnitude of tension force and the magniture of the acceleration.

The diagram shows force diagrams for both blocks. While drawing arrows in the diagram, I assumed for the moment that block 1 has axcceleration pointed down. It also takes into account the constraint in the system that the magnitude of acceleration of block 1 is equal to that of block 2, even though the directions of the acceleration vectors are different.

The diagram also displays a fundamental assumption - the ideal pulley assumption, by which we mean that the tension on the two sides of the pulley have the same magnitude.

With the positive \(y \) axis pointed up, we get the follwing two equations of motion.

With \(a_y = -a \) for block 1, the equation of motion for block 1 is

\begin{align*} \amp T - m_1 g = -m_1 a, \end{align*}

and, with \(a_y = a \) for block 2, he equation of motion for block 2 is

\begin{align*} \amp T - m_2 g = m_2 a. \end{align*}

We can easily solve these equations for \(a \) and \(T \text{.}\)

\begin{gather*} a = \dfrac{m_1 - m_2}{m_1 + m_2}\, g,\\ T = \dfrac{m_1m_2}{m_1 + m_2}\, g. \end{gather*}

Using the numerical values, we get

\begin{gather*} a = \dfrac{8 - 2}{8 + 2}\times 9.81 = 5.89\text{ m/s}^2,\\ T = \dfrac{8\times 2}{8 + 2}\times 9.81 = 15.7\text{ N}. \end{gather*}

Solution 2. c

Using constant acceleration for zero initial speed, we get

\begin{equation*} h = \dfrac{1}{2} a t^2 = \dfrac{1}{2} \times 5.89\times 0.25^2 = 0.184\text{ m}. \end{equation*}

Exercises 6.17.3 Exercises

1. Force Between Two Books Stacked with One Book Pushed from Side.

Two books are stacked on a table and the lower book is pushed with a force \(F\) horizontally as shown in Figure 6.93. Suppose \(\mu_{s12}\) and \(\mu_{k12}\) are the coefficients of static and kinetic kinetic frictions between the two books and \(\mu_{s1}\) and \(\mu_{k1}\) are the coefficients of static and kinetic kinetic frictions between the lower book and the table surface.

(a) If the two books slide on the table together, what will be their acelleration?

(b) If top book slides with respect to bottom book with both books moving, what will their separate accelerations?

(c) Suppose you start to push at lower book with increasing force, from say force \(F=0\text{,}\) you find that the two books start to accelerate together on the table upto a maximum acceleration. If you push with a higher force than that, top book slides on the bottom book. Find the value of \(F\) when tat happens.

Hint.

(a) Treat the two books as one system. (b) Treat the two books as two systems and make sure the friction and the normal force between the books work in opposite directions when acting on the two books. (c) Think about what force is responsible for aqccelerartion

Answer.

(a) \(\frac{F - \mu_{k1}(m_1+m_2)g}{ (m_1 + m_2) }\text{,}\) (b) \(\frac{F - \mu_{k1}(m_1 + m_2)g - \mu_{k12}m_2 g}{m_1},\ \ \mu_{k12}g\text{,}\) (c) \(\mu_{s12}\,g\text{.}\)

Solution 1. (a)

When books move together, the problem is same as a problem of one book of their combined mass on the table. From the forces shown in the figure we can immediately write equations of motion.

\begin{align*} \amp F - \mu_{k1}N = (m_1 + m_2) a\\ \amp N - (m_1+m_2)g = 0 \end{align*}

Therefore, acceleration is

\begin{equation*} a = \frac{F - \mu_{k1}(m_1+m_2)g}{ (m_1 + m_2) }. \end{equation*}

Solution 2. (b)

When the two books slide with respect to each other, we should look at force diagram for each book separately as shown in Figure 6.95.

The important things to notice is that normal force on book 2 is by book 1 and therefore, its pair must act on book 1 downward. Similarly, friction on book 2 must also act on book 1, but in opposite direction to how it does on book 2. From the forces shown in the figure we can immediately write equations of motion.

\begin{align*} \amp F - \mu_{k1}N_{1} - \mu_{k12}N_{12} = m_1 a_1\\ \amp N_1 - N_{12} - m_1 g = 0\\ \amp \mu_{k12}N_{12} = m_2 a_2\\ \amp N_{12} - m_2 g = 0 \end{align*}

First we get \(N_{12}\) from the last equation. Then, we use it to get \(a_2\) and \(N_1\text{.}\) Then we get \(a_1\text{.}\)

\begin{align*} a_2 \amp = \frac{\mu_{k12}m_2 g}{ m_2} = \mu_{k12}g.\\ a_1 \amp = \frac{F - \mu_{k1}N_{1} - \mu_{k12}N_{12}}{m_1}\\ \amp = \frac{F - \mu_{k1}(m_1 + m_2)g - \mu_{k12}m_2 g}{m_1} \end{align*}

Solution 3. (c)

Let’s look at when book at the top moves with the book at the bottom without sliding between them. The force that is responsible for the acceleration of the book at the top is the static force between the books. We know that static force has a maximum value.

\begin{equation*} F_{s12}^\text{max} = \mu_{s12} N_{12}, \end{equation*}

with \(N_{12}=m_2 g\) as from Figure 6.95. Therefore, maximum acceleration before sliding will be

\begin{equation*} a_\text{max} = \frac{\mu_{s12} N_{12}}{m_2} = \mu_{s12}\,g. \end{equation*}

2. A Block Pushed on Another Block and Held in Place by Static Friction.

Figure 6.96 shows a block of mass \(m\) being pushed horizontally by a force \(\vec F\) onto another block of mass \(M\text{.}\) While the two blocks move together, block \(m\) does not slide down.

The coefficient of static friction between \(m\) and \(M\) is \(\mu_s\) and the coefficient of kinetic fricton between \(M\) and the table is \(\mu_k\text{.}\) Find an expression of minimum magnitude of force \(F\text{.}\)

Hint.

(1) The block is supported by static friction force. (2) Write equations of combined system, and equations of motion for the block \(m\) only.

Answer.

\(\left( \frac{1}{\mu_s} - \mu_k\right)\; \left(1+ \frac{m}{M}\right)\;m\; g\text{.}\)

Solution.

Figure 6.97 shows force diagrams for two systems - the left panel is for the combined system and the right panel is that of a system that has mass \(m\) only. Since \(m\) does not slide down, the two systems will have the same acceleration with respect to the table. Since, we seek minimum magnitude of \(F\text{,}\) we will the condition that the static friction force between \(m\) and \(M\) is maximum as shown in the diagram by the use of \(\mu_s N'\) for this force.

Using the axes shown, we get the following \(x\) and \(y\) component of the combined motion.

\begin{align*} \amp F - \mu_k N = (M+m)A \\ \amp N - (M+m)g = 0 \end{align*}

And the following \(x\) and \(y\) component for motion of \(m\) alone. Note the direction of normal on \(m\) is horizontal here since the surface of contact is vertical.

\begin{align*} \amp F - N' = mA \\ \amp \mu_s N' - mg = 0 \end{align*}

From the first set we get

\begin{equation*} F - \mu_k (M+m)g = (M+m)A, \end{equation*}

and from the second set

\begin{equation*} F - \frac{mg}{\mu_s}= mA. \end{equation*}

From these, we can eliminate \(A\) to get

\begin{equation*} F = \left( \frac{1}{\mu_s} - \mu_k\right)\; \left(1+ \frac{m}{M}\right)\;m\; g. \end{equation*}

3. Coupled Motion of Two Blocks and an Ideal Pulley.

Two blocks of mass \(m_1 \) and \(m_2 \) are conncted by a string that goes over an ideal pulley as shown in Figure 6.98.

By ideal pulley, we will mean that the tensions on the two sides of the pulley can be assumed to have same magnitude. Block 1 is sliding on a horizontal table and block 2 is hanging. The coefficient of kinetic friction of block 1’s bottom surface and the table is \(\mu_k\text{.}\)

(a) Find the acceleration of the two blocks.

(b) Find the magnitude of tension in the string.

Check your answer for the following values: \(m_1 = 8.0\text{ kg}\text{,}\) \(m_2 = 2.0\text{ kg}\text{,}\) \(\mu_k = 0.15\text{,}\) \(\Delta t = 0.75\text{ s}\text{.}\)

Hint.

(a) and (b) Set up equations of motion for block 1 and block 2 separately using same values for the magnitudes of tension and acceleration. (c) Use constant-acceleration equations.

Answer.

(a) \(0.785\,\text{ m/s}^2\text{,}\) (b) \(18.1\text{ N}\text{,}\) (c) \(0.221\text{ m}\text{.}\)

Solution 1. (a) and (b)

(a) and (b). We will write equations of motions of the two blocks by working \(\vec F = m\vec a \) for each, with two common values, the magnitude of tension force and the magniture of the acceleration. Figure 6.99 shows force diagrams for both blocks.

Figure 6.99. Figure for Exercise 6.17.3.3 (a) and (b).

Note that block 1 will have two equations of motion and block 1 will give one. Equations of motion for block 1 are

\begin{align} \amp T-\mu_k N = m_1 a,\tag{6.35}\\ \amp N - m_1 g = 0,\tag{6.36} \end{align}

and, since for block 2, we have \(a_y = -a \text{,}\) taking the magnitude \(a \) as positive, equation of motion for block 2 is

\begin{equation} T - m_2 g = - m_2 a.\tag{6.37} \end{equation}

Solving (6.35)-(6.37) we can get

\begin{align*} \amp a = \dfrac{m_2 -\mu_k\,m_1}{m_1 + m_2}\ g,\\ \amp T = \dfrac{(1+\mu_k)\,m_1\,m_2}{m_1 + m_2}\ g. \end{align*}

Using the given numerical values we will get

\begin{align*} \amp a = \dfrac{2 -0.15\times8}{8 + 2}\times 9.81 = 0.785\,\text{ m/s}^2,\\ \amp T = \dfrac{(1+0.15)\times 8 \times 2}{8 + 2}\times 9.81 = 18.1\text{ N}. \end{align*}

Solution 2. (c)

(c) We can use the constant-acceleration formulas to find \(|\Delta y| \) of block 2 since we know the acceleration. We use the following equation

\begin{equation*} \Delta y = v_{i,y}\Delta t + \dfrac{1}{2}a_y(\Delta t)^2, \end{equation*}

with \(v_{i,y} = 0\) and \(a_y = -a \text{.}\) Height \(h \) is the absolute value of \(\Delta y\text{.}\)

\begin{equation*} h = \dfrac{1}{2}\, \dfrac{m_2 -\mu_k\,m_1}{m_1 + m_2}\ g\, (\Delta t)^2. \end{equation*}

The numerical values give us

\begin{equation*} h = \dfrac{1}{2}a(\Delta t)^2 = \dfrac{1}{2} 0.785 \times \times 0.75^2 = 0.221\text{ m}. \end{equation*}

4. Block on Incline of an Accelerating Wedge.

Figure 6.106 shows a block of mass \(m\) sliding on a wedge of mass \(M\) with incline \(\theta\text{.}\) As observed from a fixed frame \(Oxy\text{,}\) the wedge has acceleration \(A\) horizontally towards positive \(x\) axis and the block has acceleration \(a\) pointed down the incline.

Assuming zero friction between the block and wedge and between wedge and the table, find expressions for \(a\) and \(A\text{.}\)

Hint.

Draw two figures - one for forces on block and one for forces on wedge. Make sure you include normal from block onto wedge correctly using Newton’s third law. Use an inertial frame, say a frame attached to the table, not to the wedge.

Answer.

See solution.

Solution.

When using \(\vec F = m\vec a\text{,}\) we need to be cognizant of the fact that this is valid only with respect to an inertial frame - if coordinate system is attached to an accelerating object, then this equation is modified appropriately. Here, we should attach coordinate to the table and to the wedge as shown in Figure 6.101.

Figure 6.101. Left panel: Forces on the block and its free-body diagram. Right panel: Forces on the wedge and its free-body diagram. Notice the normal force between wedge and block, \(N\text{,}\) has opposite direction when acting on block and when acting on wedge as required by Newton’s third law.

Let \((X(t),0)\) be coordinates of the tip of the wedge and \((x(t), y(t))\) coordinates of the block at instant \(t\text{.}\) then, from the geometry of the wedge, we have the following relation.

\begin{equation*} \tan\theta = \frac{y}{x-X}, \end{equation*}

which can be written as

\begin{equation*} y \cos\theta = x \sin\theta - X \sin\theta. \end{equation*}

Now, taking two derivatives with respect to \(t\text{,}\) w obtain the following relation among components of acceleration of the block and the wedge.

\begin{equation} a_y \cos\theta = a_x \sin\theta - A_x \sin\theta.\tag{6.38} \end{equation}

Now, from the free-body diagram of the block we get

\begin{align} \amp -N\sin\theta= m a_x,\tag{6.39}\\ \amp N\cos\theta - m g = m a_y.\tag{6.40} \end{align}

Similarly, the free-body diagram of the wedge gives

\begin{align} \amp N\sin\theta = M A_x,\tag{6.41}\\ \amp N' - Mg - N\cos\theta - m g = 0.\tag{6.42} \end{align}

These are 5 equations in 5 unknowns: \(a_x, a_y, A_x, N, N'\text{.}\) Thus, by eliminating \(N\) and \(N'\) we can solve for \(A_x\text{,}\) \(a_x\) and \(a_y\text{.}\) From these we will get the final answer as

\begin{equation*} A = |A_x|,\ \ a = \sqrt{a_x^2 + a_y^2}. \end{equation*}

Now, to do the calculations, we notice that from Eqs. (6.39) and (6.41), we get

\begin{equation} MA_x = - m a_x.\tag{6.43} \end{equation}

This is actually a statement of conservation of linear momentum along \(x\)-axis since external forces are only along the \(y\)-axis. From Eqs. (6.39) and (6.40), we get

\begin{equation} a_x\cos\theta + a_y\sin\theta = -- g \sin\theta.\tag{6.44} \end{equation}

From Eqs. (6.43) and (6.38), we get

\begin{equation} a_y\cos\theta = \left( 1 + \frac{m}{M}\right)a_x\sin\theta.\tag{6.45} \end{equation}

Using Eq. (6.45) in (6.44) gives us equation from which we can get \(a_x\text{.}\)

\begin{equation*} a_x \cos\theta + \frac{1}{\cos\theta} \left( 1 + \frac{m}{M}\right)a_x\sin^2\theta = - g \sin\theta. \end{equation*}

Hence,

\begin{equation} a_x = \frac{-g\sin\theta\cos\theta}{ 1 + \frac{m}{M}\sin^2\theta }.\tag{6.46} \end{equation}

This into Eq. (6.45) gives

\begin{equation} a_y = \left( 1 + \frac{m}{M} \right)\tan\theta a_x.\tag{6.47} \end{equation}

Finally, \(A_x\) will be

\begin{equation} A_x = - \frac{m}{M} a_x.\tag{6.48} \end{equation}

5. Block not Sliding on Frictionless Wedge.

Figure 6.102 shows a block of mass \(m\) on a wedge of mass \(M\) with incline \(\theta\text{.}\) The surface of contact between the block and wedge is frictionless.

Normally, a block under this condition would slide. But, if wedge has a horizontal force \(\vec F\) of a specific magnitude, the block will not slide; instead block and wedge would just move together as if block was glued to the wedge. Find the magnitude of this force.

Hint.

Draw two free-body diagrams, one for block and another for wedge.

Answer.

\((m + M)g\;\tan\theta\text{.}\)

Solution.

As in Figure 6.101, we draw free-body diagrams of block and wedge, making sure we take care of normal force between block and wedge appropriately. For more detail, see Exercise 6.17.3.4. For the current problem, FBD for both block and wedge are shown in Figure 6.103. For block not to slide, block must have same acceleration as the wedge with respect to fixed frame \(Oxy\text{.}\)

Using the coordinate system \(Oxy\text{,}\) we get equations for the block to be

\begin{align*} \amp -N \sin\theta = -m A. \\ \amp N \cos\theta - mg = 0. \end{align*}

This will give

\begin{align*} \amp N = \frac{mg}{\cos\theta} \\ \amp A = g\tan\theta. \end{align*}

Using the coordinate system \(Oxy\text{,}\) we get equations for the wedge to be

\begin{align*} \amp -F + N \sin\theta = -m A. \\ \amp N' - N \cos\theta - Mg = 0. \end{align*}

Using \(A\) and \(N\text{,}\) we get

\begin{equation*} F = (m + M)g\;\tan\theta. \end{equation*}

6. Block not Sliding in Motion of Three Blocks and a Pulley.

Figure 6.104 shows three blocks whose motion is coupled through a string that goes over an ideal (massless, frictionless) pulley. If there is no friction between blocks 1 and 2, block 2 will just stay put with block 1 sliding away from underneath it.

Assuming no friction between block 1 and the table, find the minimum coefficient of static friction between blocks 1 and 2 so that block 1 does not slide from under block 2.

Hint.

(1) Use maximum static friction between 1 and 2. (2) You wil need three free-body diagrams.

Answer.

\(\mu_s = \frac{m_3}{m_1 + m_2 + m_3} \text{.}\)

Solution.

Figure 6.105 shows three force diagrams for this problem. One is for the combined systems of \((m_1+m_2)\text{,}\) another one for \(m_1\text{,}\) and the third one is for \(m_3\text{.}\) Since pulley is ideal, we use the tension on the two sides of the pulley has same magnitude.

Since, we want block 2 not to slide on 1, magnitude of acceleration for 1 and 2 must be same. Since string’s length is not changing during motion, acceleration of all three blocks will have same magnitude. that explains the choice of same symbol. Since, we seek minimum \(\mu_s\) between 1 and 2, we will use \(maximum\) static friction between them. Also, note that this static friction has the direction same as the direction of acceleration when acting on block 2.

Working with horizontal and vertical coordinates in the frame of the table, we get the following equations for the combined system,

\begin{align*} \amp T = (m_1 + m_2)A \\ \amp N - (m_1 + m_2)g = 0 \end{align*}

for the \(m_2\) system,

\begin{align*} \amp \mu_s N' = m_2 A \\ \amp N' - m_2 g = 0 \end{align*}

and for the \(m_3\) system

\begin{equation*} T - m_3 g = - m_3 A. \end{equation*}

We eliminate, \(T,\ N',\ A\) from these to get

\begin{equation*} \mu_s = \frac{m_3}{m_1 + m_2 + m_3}. \end{equation*}

We do not have any use of \(N\) in this problem.

7. Practice with a Friend: Coupled Motion of Two Blocks on Two Sides of a Fixed Wedge.

Figure 6.106 shows two blocks on two inclines. Assuming surfaces to be frictionless, the wedge to be fixed in its place, tension to be same througout the string, and the acceleration direction as shown to be correct, find the magnitude of acceleration and tension in the string.

Answer.

\(a = \left( \frac{m_2\sin\theta_2 - m_1\sin\theta_1 }{m_1 + m_2}\right)\; g.\text{.}\)

8. Practice with a Friend: Block on Incline of an Accelerating Wedge.

In Exercise 6.17.3.4, we assumed that there is no friction between wedge and table and between wedge and block. Now, we relax these assumptions. Let static friction coefficient between wedge and table be \(\mu_{wt}\) while the surface between wedge and block still remain frictionless.

Let us now assume that angle of inclination \(\theta\) is adjustable. You will find that up to some angle \(\theta_c\text{,}\) block just slides down the incline without the wedge moving on the table. When you exceed this angle, the wedge starts to slide on the table. Find an expression for this critical angle.

Prev Top Next