Section 35.3 Existence of Magnetic Field
From our demonstrations presented above, it is obvious that magnetic force between magnets act at a distance - meaning magnets do not have to touch each other. However, it seems unreasonable for a force to propagate between magnets without anything between them; of course, we have a similar situation for gravity and electric forces.
Michael Faraday came up with an alternative explanation “to explain” how a magnet could influence another magnet at a distance. He imagined that each magnet sets up a field, which we call magnetic field, in space around it regardless of whether there is anything else in that space. When you place another magnet in that field, it just responds to the field at its own location, and in an indirect way to the magnet that set up the field in the first place.
This is similar to the field-based explanation of the action-at-distance behavior of electric and gravitational forces. However, unlike electric and gravitational fields, you can easily visualize the magnetic field of a magnet by sprinkling iron filings near the magnet as shown in Figure 35.9. The iron particle get magnetized in a magnetic field and stick together along magnetic field lines as seen in the picture.

Magnetic field will be denoted by \(\vec B \text{.}\) You can determine the directions of magnetic field vectors in space by placing magnetic compass at space points near the magnet. We will discuss a method for finding the magnitude of the magnetic field in the next section.
When you connect the magntic field directions, we get magnetic field lines. Outside a magnet, magnetic field lines come out of the North pole and land on the South pole as illustrated for a bar magnet in Figure 35.10. But inside the magnet, they continue from the south-end of the microscopic magnet to its north-end. That means, inside a magnet the direction of magnetic field lines go from the South pole to the North pole.
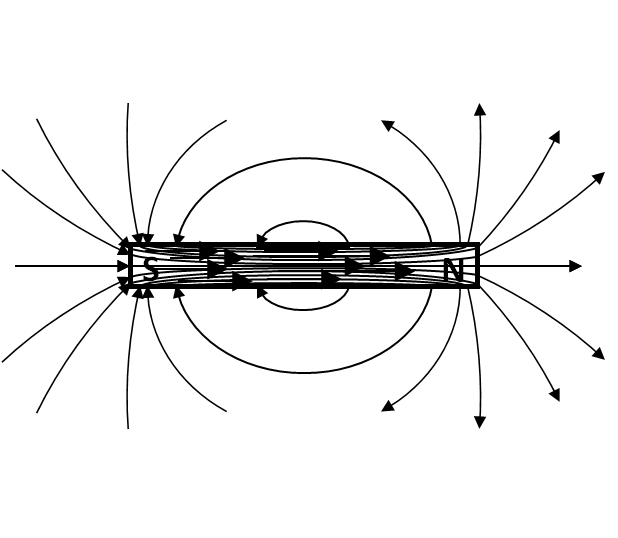
When drawing magnetic field lines, we represent strength of the magnetic field in the region by drawing sufficient number of lines so that the “density of lines” corresponds to the strength of the magnetic field in the region. This is similar to how we represent strength of electric field in electric field lines. Thus, the density of lines is higher near the poles of a magnet than far away from the poles, and it is highest inside the magnet since all lines must pass through the magnetic body.
When magnetic field lines are straight, then the direction of the lines are the direction in which a magnetic needle will point in the direction of South-to-North when placed at that point. If the lines are curved, then the tangent to magnetic field lines gives us the direction in which a tiny magnetic needle will point if placed there.
Subsection 35.3.1 Magnetic Field of Current Carrying Wire
In April of 1820 Hans Christian Øersted of the University of Copenhagen discovered that electric currents also exert magnetic force on magnetic needles. Actually, you can also demonstrate that one current carrying wire exerts force on another current carrying wire, neither of which are magnetic material, as we will see below.
The magnetic force on a magnet by a current carrying wire is indistinguishable from the magnetic force of another magnet. Therefore, to understand the magnetic force of a current carrying wire, we say that electric current has magnetic field just like the magnetic field of other magnets.
The effect of current in a straight wire was shown to align magnetic needles such that they pointed along circles around the current-carrying wire. This says that the magnetic field lines of a straight wire with a current are circles around it as shown in Figure 35.7. These fields are not like that of a field of a bar magnet. To get something similar to that of a bar magnet we need to look at magnetic field of coils. It turns out that magnetic field of tightly-wound coil of wire carrying current is more like the magnetic field of a bar-magnet as shown in Figure 35.11.
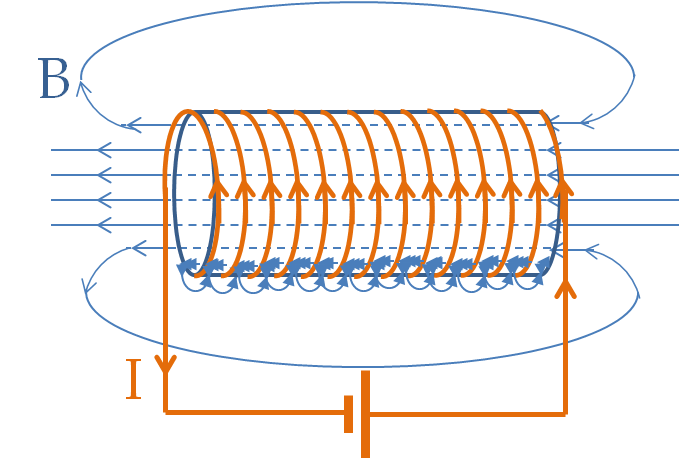
The magnetic field of current through coils is straight near the middle of the loops. If the coils are tightly wound, then the magnetic field on the sides are nearly zero and one obtains uniform magnetic field inside the space enclosed by the coils. You can try to see how these magnetic field lines remind you of fields of a bar magnet and help explain the attraction and repulsion of magnet shown in Figure 35.8. In the next chapter we will perform calculations that gives us formulas for these magnetic fields. Here, we are just getting our feet wet.

