Types of Stress and Strain

Section 16.3 Types of Stress and Strain

Subsection 16.3.1 Tensile and Compressive Stresses

A stress that causes strain in the same direction as the applied force can lead to either the extension of the body or a compression of the body as illustrated in Figure 16.25.

The stress that leads to an extension of the body is called a tensile stress and the stress that compresses the body is called a compressive stress.

Figure 16.25. If the strain in the material is negative, i.e. the material is compressed as a result of the stress, then the stress is called a compressive stress. If the strain in the material is positive, i.e. the material stretches as a result of the stress, then the stress is called a tensile stress.

Usually Young’s moduli for the two stresses are equal, but they do not have to be equal. For instance, Young’s modulus for concrete is \(2\text{MPa}\) for the tensile stress and 20 MPa for the compressive stress. Thus, a column made of concrete will break more easily when pulled than when compressed; a concrete column is able to support considerably more weight on the column than it can hold up weight hanging from it.

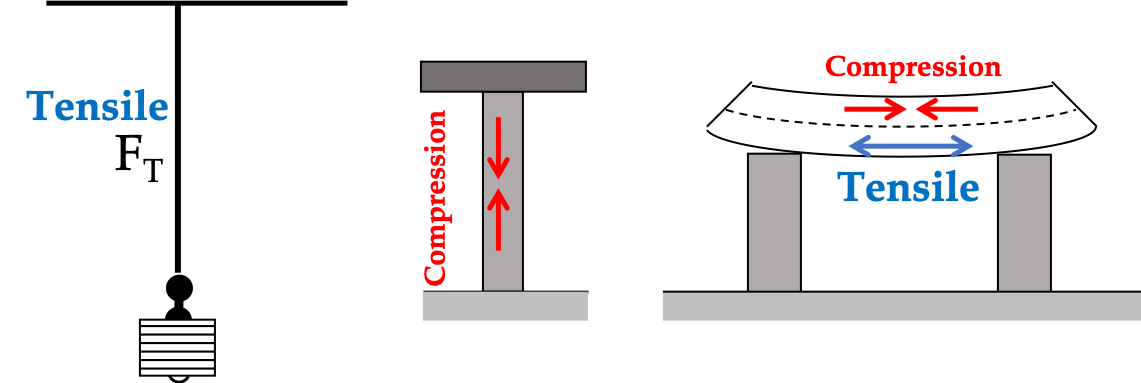
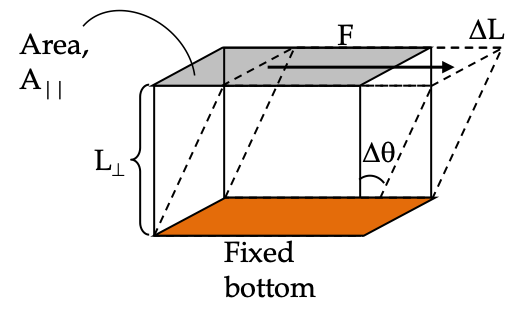
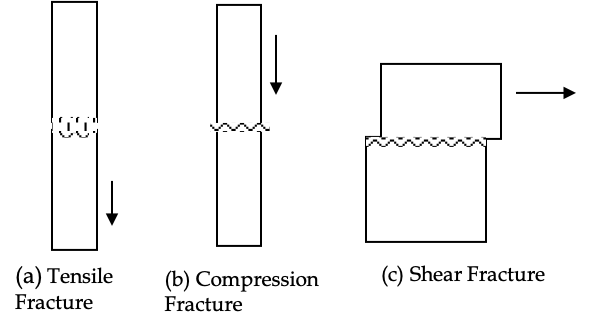
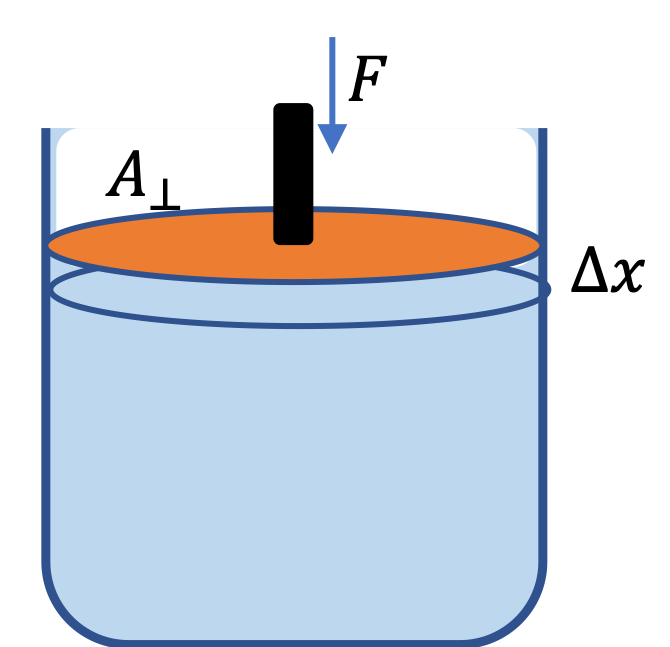
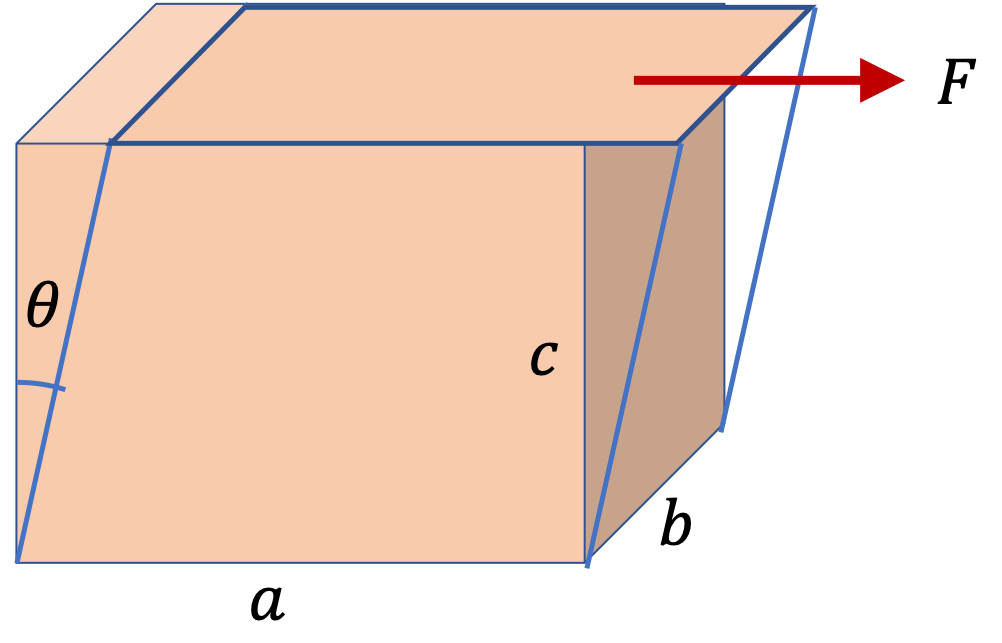
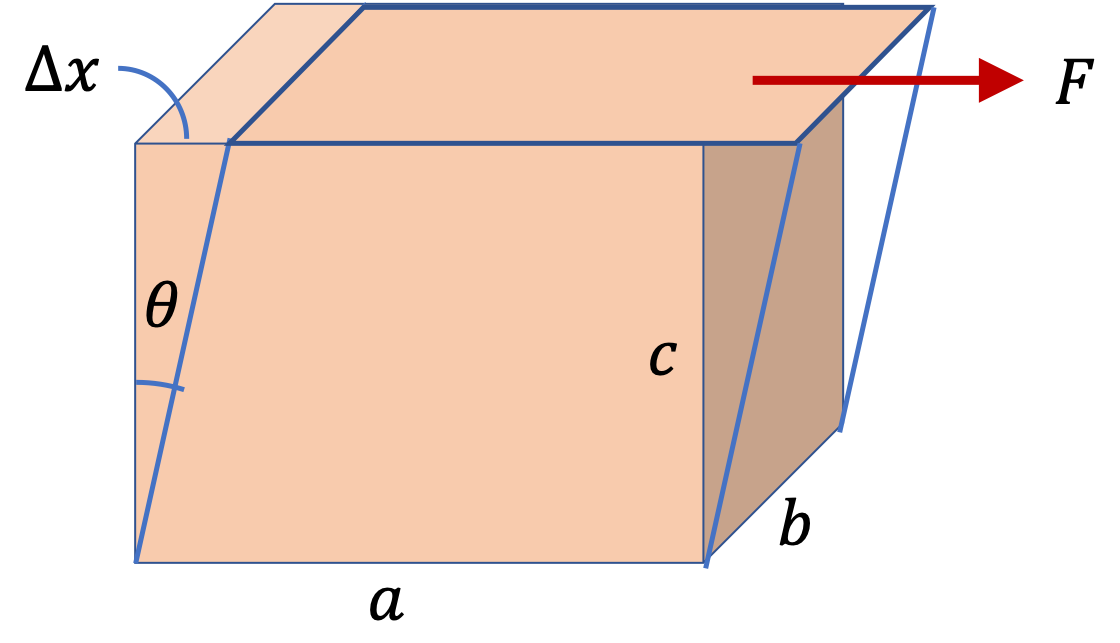
Example 16.26. Stress in a Steel Beam.

A steel beam of length \(L\) and area of cross-section \(A\) is posted vertically on a concrete slab. Find the tensile stress in the beam as a function of height \(h\text{.}\)

Answer.

\(\frac{Mg}{AL}(L-h)\)

Solution.

We have done a similar problem for a wire under stress. Same technique will give the stress at any point equal to the weight of the steel beam above that point. Suppose the origin of the \(y\) coordinate is at the top point of the beam and the direction of the \(y\) axis is pointed down. Then, the weight of the beam above the point with \(y\) coordinate equal to \(y\) will be \(M gy/L\text{.}\) Therefore, the stress at that point will be

\begin{equation*} \text{Stress at a distance from the top } = \frac{Mg}{L}y/A. \end{equation*}

We can state the answer for the height from the bottom as

\begin{equation*} \text{Stress at a height h from the bottom } =\frac{Mg}{AL}(L-h). \end{equation*}

Subsection 16.3.2 Shear Stress

When a force is applied parallel to the surface of an object, instead of stretching or compressing the object, the force may deform the object if some other part of the object is held fixed. For instance, suppose you fix the bottom of a box by gluing the bottom part and apply a side-ways force on the top part as illustrated in Figure 16.27, you will deform the box. This deformation is used to define an angular or shear strain.

Figure 16.27. Shear stress develops inside the material when it is deformed sideways by applying a force on one face while keeping the opposite face fixed.

The shear strain is defined by angle \(\Delta \theta\) by which one face has been moved reltative to the opposite face. For small deviations, the angle of the deviation \(\Delta \theta\) is equal to \(\Delta L/L_{\perp}\) as shown in Figure 16.27.

\begin{equation} \Delta \theta \approx \tan(\Delta\theta) = \frac{\Delta L}{L_{\perp}}.\tag{16.46} \end{equation}

The resulting stress in the body is called shear stress. Note where applied force is acting: it is spread over the area of the surface parallel to the force and not perpendicular to the force, which was the case for the tensile and compressive stresses. Therefore, stress corresponding to a shear strain is defined by the magnitude of the force \(\vec F\) divided by parallel area, \(A_{\parallel}\text{.}\)

\begin{equation} \text{Shear stress} = \frac{F}{A_{\parallel}}.\tag{16.47} \end{equation}

Hooke’s law is also applicable for this situation if strain is small. That is, we expect the shear stress to be proportional to the shear strain.

\begin{equation} \text{Shear stress} = G\times \textrm{Shear strain}\tag{16.48} \end{equation}

where the proportionality constant \(G\) is called the shear modulus of the material. The shear modulus \(G\) has the units of \(\text{N/m}^2\) or \(\text{Pa}\text{.}\) As a general rule, the shear modulus is less than the Young’s modulus for the same material, which means that it is usually easier to deform an object sideways than to compress or elongate it.

Note that you must pay attention to the particular area and length in the definition of shear stress given in Eq. (16.47). Unlike the tensile stress, the area here is of the surface that is parallel to the applied force. Furthermore, when you find angle of deviation to use in the formula for the the angular deviation, you need to make sure the displacement \(\Delta L\) and the length \(L_{\perp}\) are perpendicular to each other. Also, note that, while \(\Delta L\) is parallel to the applied force, \(L_{\perp}\) is perpendicular to the applied force.

Example 16.28. Shear Strain of Spinal Disk.

Spinal injuries often involve shear stress on the spinal disks. Find the deformation of a spinal disk if it is subjected to \(500\text{-N}\) shear force. Assume the disk to be a solid cylinder \(4.0\text{ cm}\) in diameter and the force applied over the area of cross-section.

Use shear modulus of spine disk = \(1.2\text{ GPa}\text{.}\)

Answer.

\(3.3\times 10^{-4}\text{ rad}\text{.}\)

Solution.

Let \(\Delta\theta\) be the shear strain. Using the relation of stress and strain we get

\begin{equation*} \Delta\theta = \dfrac{\sigma}{G}, \end{equation*}

with stress given by

\begin{equation*} \sigma = \dfrac{500\text{ N}}{\pi (0.02)^2\text{ m}^2} = 4.0\times 10^5\text{ Pa}. \end{equation*}

Therefore, shear strain is

\begin{equation*} \Delta\theta = \dfrac{4.0\times 10^5\text{ Pa}}{1.2\times 10^9\text{ Pa}} = 3.3\times 10^{-4}\text{ rad}. \end{equation*}

Subsection 16.3.3 Ultimate Strength

I have mentioned above that if stress exceeds a certain value, the material will ultimately break up. This was illustrated in Figure 16.19 for stretching of a wire. We expect the same physics should happen for the compressive, tensile, and shear stresses.

The compressive, tensile, and shear stresses lead to three kinds of fractures in materials, called tensile fracture, compressive fracture and shear fracture, as displayed in Figure 16.29.

Figure 16.29. Compressive, tensile and shear fractures.

Note than the shear stress rupture is in the perpendicular dimension to the direction of the shear force while the tensile or compression related ruptures take place in the same direction as the corresponding force. The ultimate stress of each type that a material can withstand before giving in is called the ultimate strength of the material.

Whenever you design a mechanical structure, you must take into account the ultimate strength of the material to be used and the type of stress to be expected under extreme conditions of use. This is especially important when designing the structures that are subject to large stresses such as buildings and bridges. The ultimate strength for the shear stress is usually less than that for compressive and tensile stresses.

Subsection 16.3.4 Pressure

We have looked at stresses caused in solid material by forces applied perpendicular to the opposite faces of the material and those applied parallel to the surfaces of the material. You can cause stress in a fluid by applying a force that can alter its volume, e.g., by placing the fluid in a rigid container with a lid so that when you push on the fluid, fluid gets pressed from the walls of the container as well. Stress in a fluid is called pressure.

Figure on the right shows a simple way to study change in volume of a fluid. Let \(\Delta x\) be the displacement of the lid, then change in volume \(\Delta V = -A_\perp \Delta x\text{.}\) The volumetric strain, \(\epsilon\text{,}\) also called bulk strain is relative change in volume.

\begin{equation} \epsilon =\left| \dfrac{\Delta V}{V} \right|.\tag{16.49} \end{equation}

With force \(F\) pushing over an area \(A_\perp\) of the fluid, causes additional pressure to develop in the fluid, given by

\begin{equation} P = \frac{F}{A_{\perp}}.\tag{16.50} \end{equation}

Hooke’s law also holds for the pressure and the bulk strain

\begin{equation} \text{Pressure} = B \times \textrm{Bulk strain},\tag{16.51} \end{equation}

where the proportionality constant \(B\) is called the bulk modulus.

Exercises 16.3.5 Exercises

1. Compression of a Support Beam.

Two cylindrical concrete posts are to support a heavy machine of mass 20,000-kg set in the middle of a 2000-kg beam resting on the posts. For safety reasons, it is required that the stress in the posts does not exceed 5 times the ultimate strength of concrete, what must be the minimum radii of the two posts. Ultimate strength of concrete = \(20 \times 10^6\text{N/m}^2\text{.}\)

Hint.

Equate stress in concrete to one-fifth of the ultimate strength.

Answer.

\(9.27\text{ cm}\)

Solution.

Each post will support half the weight of the beam and weight. Thus, force on each concrete

\begin{equation*} F = \dfrac{1}{2}\times 22000\times 9.81 = 107910\text{ N}. \end{equation*}

This causes stress in the concrete, given by,

\begin{equation*} \text{Stress} = \dfrac{F}{A} = \dfrac{107910\text{ N}}{A}, \end{equation*}

where \(A \) is the area of cross-section of the post. We do not want this stress to be more than \(\dfrac{1}{5}\text{-th}\) of the ultimate strength.

\begin{equation*} \dfrac{107910}{A} = \dfrac{1}{5} \times 20 \times 10^6. \end{equation*}

Therefore,

\begin{equation*} A = 0.0269775\text{ m}^2. \end{equation*}

This should equal \(\pi R^2\text{.}\) Then,

\begin{equation*} R = \sqrt{0.0269775/\pi} = 0.0927\text{ m} = 9.27\text{ cm}. \end{equation*}

2. Deforming a Jello By Shear Stress.

A rectangular parallelepiped-shaped jello with dimensions \((a\times b \times c) = 5\text{ cm} \times 4\text{ cm} \times 3\text{ cm}\) is resting on a plate. A glass slide is glued to the top surface. A force of \(F = 30\text{ mN}\) is applied to the glass plate deforming the jello sideways.

(a) What is the angle of deformation if the jello has a shear modulus of \(G=1000\text{ Pa}\text{?}\)

(b) What is the displacement of the glass slide?

Hint.

(a) Area over which force acts is \(ab\text{.}\) (b) You can use small angle approximation here to simplify your calculation.

Answer.

(a) \(1.5\times 10^{-2}\text{ rad}\text{.}\) (b) \(0.45\text{ mm}\text{.}\)

Solution 1. (a)

(a) Refering to the figure given in the problem statement, we see that the area over which the force acts is

\begin{equation*} A = a b = 5\text{ cm}\times 4\text{ cm} = 20\times 10^{-4}\text{ m}^2. \end{equation*}

Therefore, the shear stress is

\begin{equation*} \dfrac{F}{A} = \dfrac{ 30\times 10^{-3}\text{ N} }{ 2.0\times 10^{-3}\text{ m}^2} = 15.0\text{ N/m}^2. \end{equation*}

The shear strain is the angle of deformation.

\begin{equation*} \theta = \dfrac{\text{ Stress}}{G} = 1.5\times 10^{-2}\text{ rad}. \end{equation*}

Solution 2. (b)

(b) Refer the figure. Note that we got small angle in (a), and we can simplify calculation by using \(\tan\theta \approx \theta\) in radians.

\begin{equation*} \Delta x = c\,\theta. \end{equation*}

Putting in numerical values we get

\begin{equation*} \Delta x = 3\text{ cm}\times 1.5\times 10^{-2}\text{ rad} = 0.45\text{ mm}. \end{equation*}

3. Tear Under Shear Stress.

A steel bolt is used to connect two steel plates. It is required that the bolt must withstand shear forces up to \(4,000\text{ N}\text{.}\) Assuming a safety factor of 5, what must be the minimum diameter of the bolt? Use breaking shear stress of steel = \(250\times 10^6\ \text{Pa}\text{.}\)

Hint.

Use stress= breaking stress/5.

Answer.

\(1.0\text{ cm}\)

Solution.

Here, the shear force divided by the area of the bolt must be one-fifth of the breaking shear stress. Let \(d \) be the diameter. Using the breaking shear stress for steel we get

\begin{equation*} \dfrac{4000\text{ N}}{\pi d^2/4} = \dfrac{250\times 10^6\text{ Pa}}{5}. \end{equation*}

Therefore, \(d = 0.01\text{ m} = 1.0\text{ cm}\text{.}\)

4. Stress and Strain in Deep Sea Diving.

While deep sea diving, one must take into account the enormous pressure at great depths under water. At \(3,000\text{-m}\) depth, the pressure would be approximately \(30\text{MPa}\text{,}\) which will crush a ball of steel. What is the percentage change in volume of a spherical solid ball of steel when it is sent to a depth of \(3,000\text{ m}\) in water?

Data: Bulk Modulus of Steel = \(166\text{ GPa}\text{.}\)

Hint.

Answer.

\(0.018%\)

Solution.

Hooke’s law for volume strain is

\begin{equation*} \text{Volume Stress } = B\, \dfrac{\Delta V}{V}. \end{equation*}

Therefore,

\begin{equation*} \dfrac{\Delta V}{V} = \dfrac{30\text{ MPa}}{166\1000\text{ MPa}} = 1.8\times 10^{-4}. \end{equation*}

Multiplying by 100, we get 0.018%.

5. Force per Unit Area on Container when Water Freezes.

A steel spherical shell is filled with water and sealed close by welding the opening. When water freezes, its volume expnads by \(9\%\) if it is allowed to expand, but due to the steel enclosing, the volume does nor expand. With what force per unit area does the ice push the steel enclosure?

Data: Bulk stress of water \(\approx 2.2\text{ GPa}\text{.}\)

Hint.

The stress in water would be equal to the stress had we shrunk it back from the expanded to the unexpanded volume.

Answer.

\(1.98\times 10^{8}\text{ Pa}\text{.}\)

Solution.

The stress \(\sigma\) in ice developed will equal the stress that would have developed had we allowed the water to expand. You might think of it this way: you first let it expand freely and then push on it to bring the volume back to the original.

\begin{equation*} \sigma = B \times \text{strain}, \end{equation*}

where

\begin{equation*} \text{strain} \end{equation*}

is the bulk strain

\begin{equation*} \text{strain} = \dfrac{\Delta V}{V} = 0.09. \end{equation*}

With \(B\) of water given, the stress will be

\begin{equation*} \sigma = 2.2\times 0.09\text{ GPa} = 1.98\times 10^{8}\text{ Pa}. \end{equation*}

This is the force per unit area exerted by the ice.

Prev Top Next