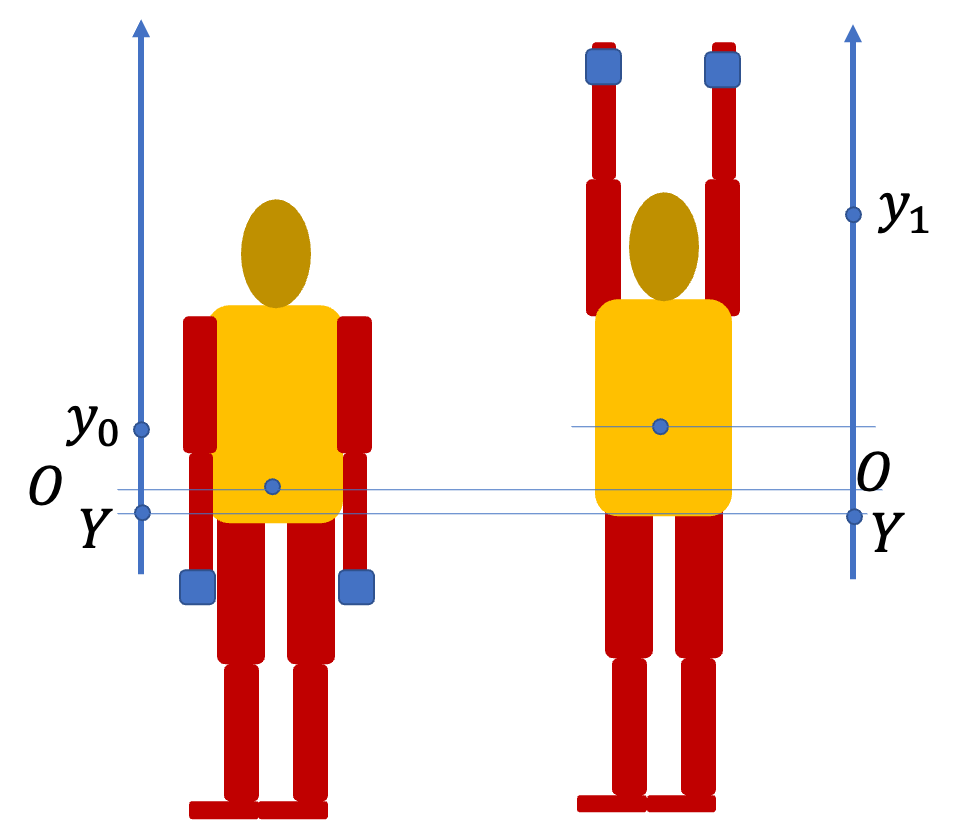
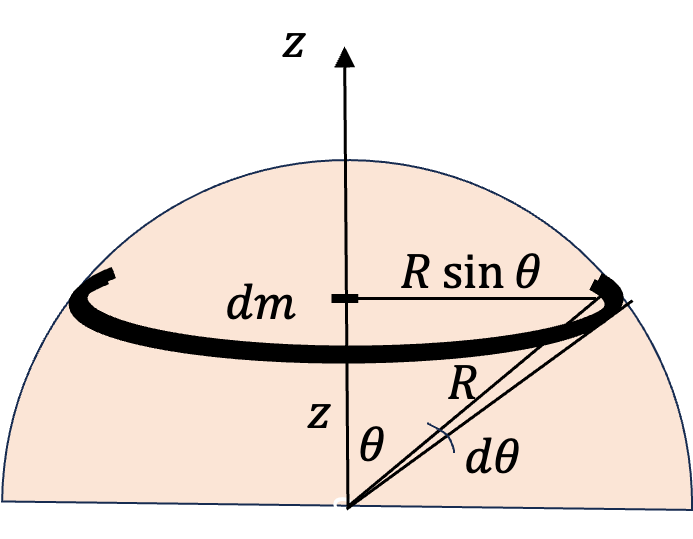
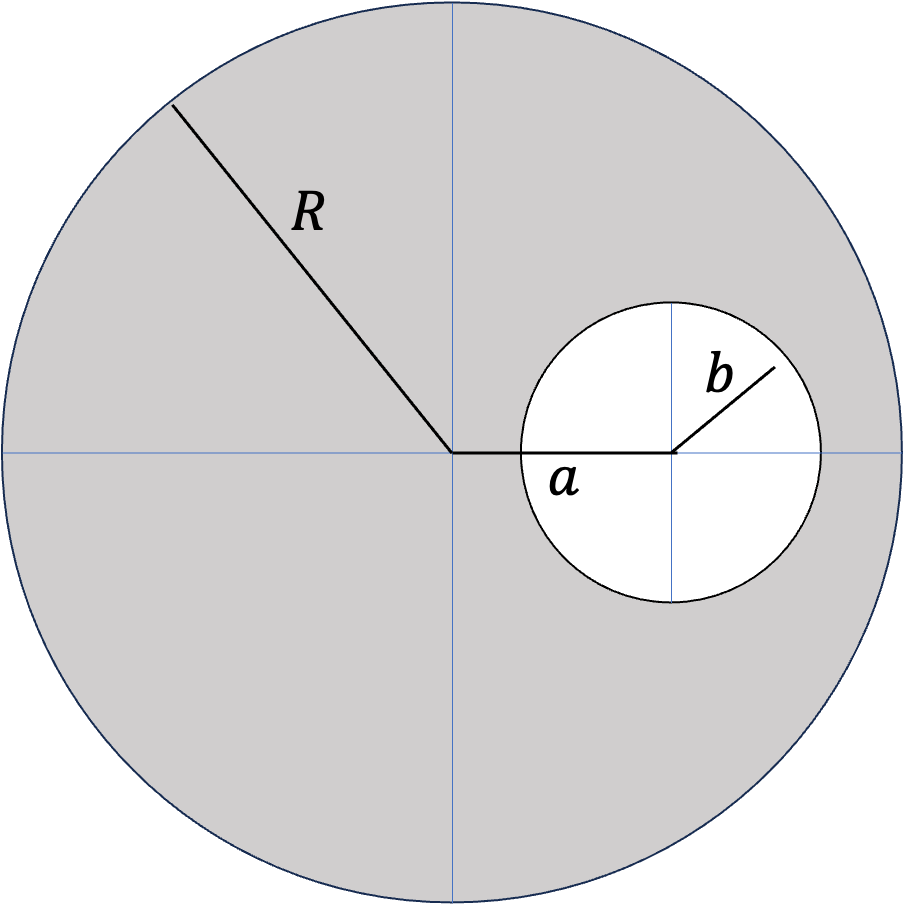
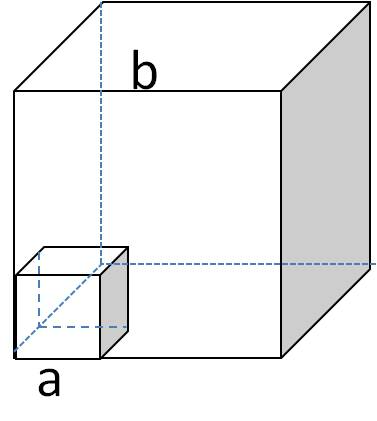
A continuous body is distributed throughout the space occupied by the material. The distribution of mass in the body is most aptly described by a mass density function, \(\rho (x,y,z)\text{,}\) which is the mass per unit volume in the neighborhood of the point \((x,y,z)\text{.}\) If the object has a uniform mass density, then \(\rho (x,y,z)\) will have the same value throughout the body. The total mass \(M\) of the body is obtained from the density function by an integral over the volume of the object.
\begin{equation*}
M = \int \rho(x,y,z) dx dy dz.
\end{equation*}
For a uniform mass density object, denoting the density by \(\rho_0\) we have
\begin{align*}
\amp \rho(x,y,z) = \rho_0, \textrm{ independent of }\\
\amp \ \ \ \Longrightarrow\ M = \rho_0 V,
\end{align*}
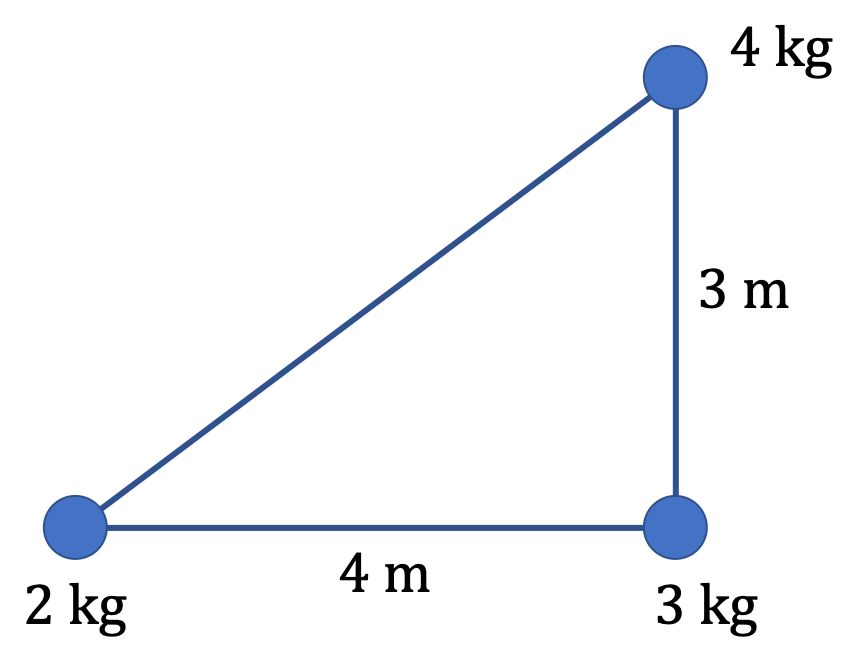
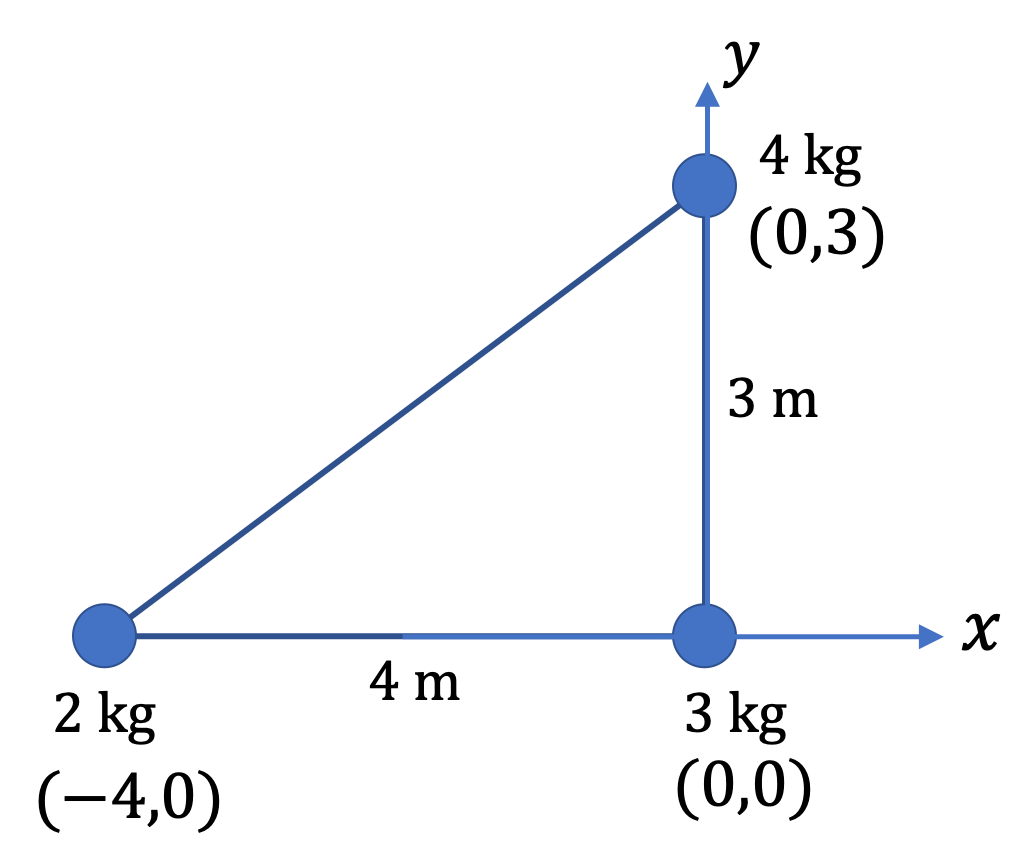
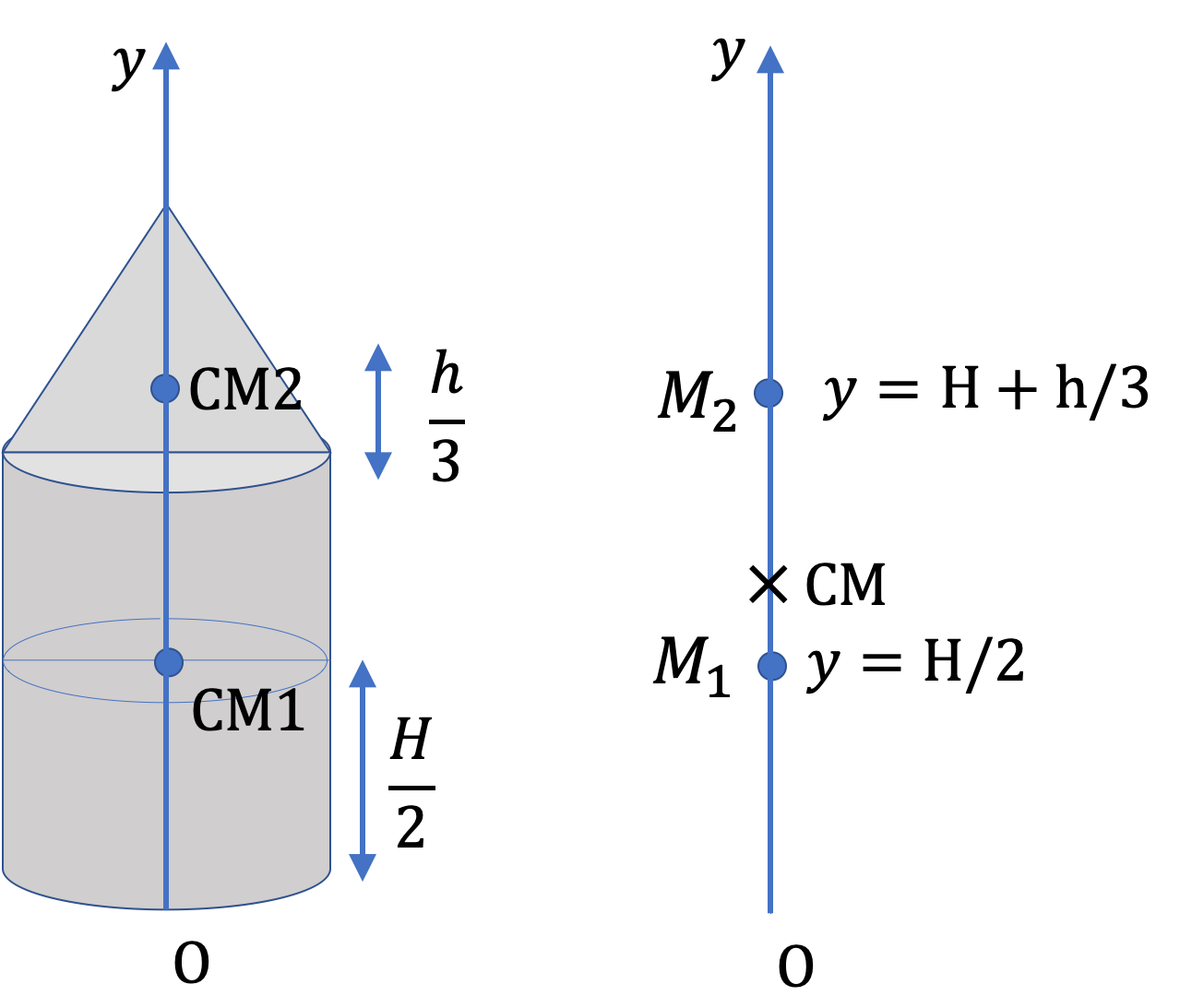
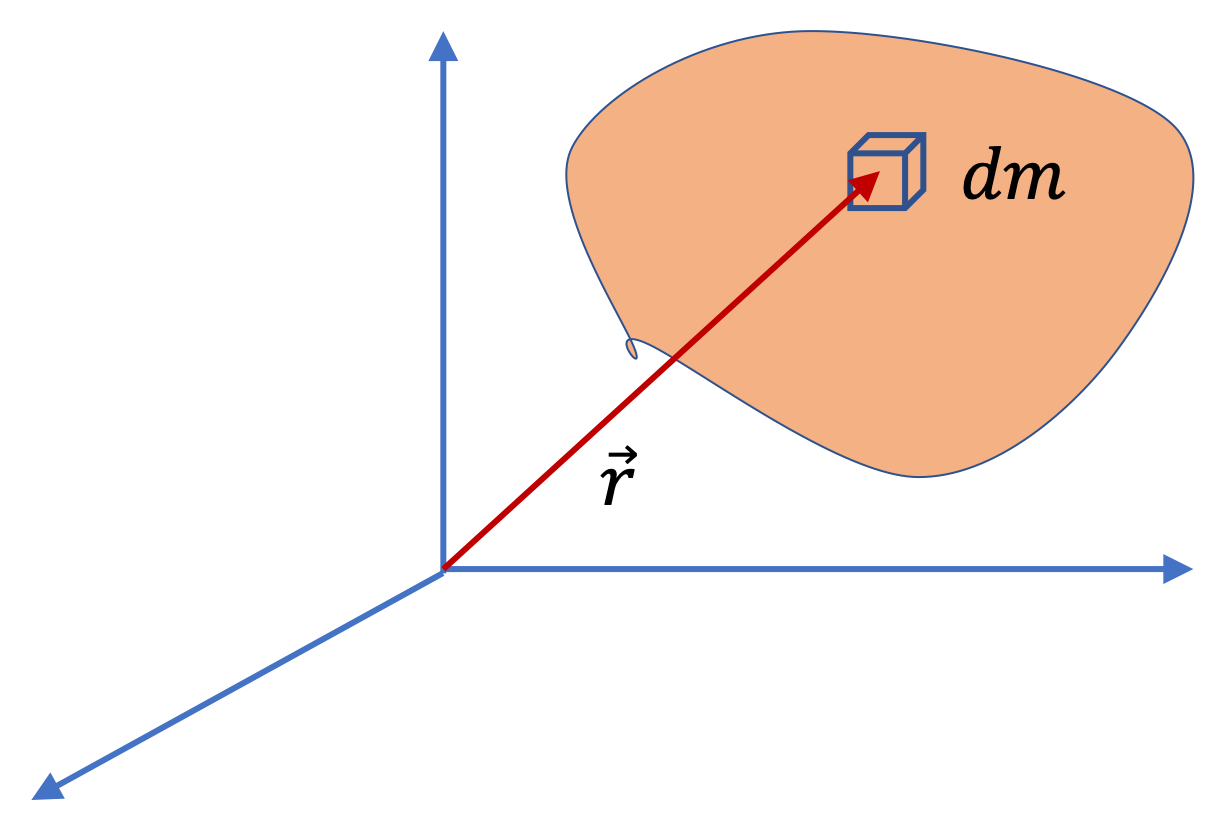
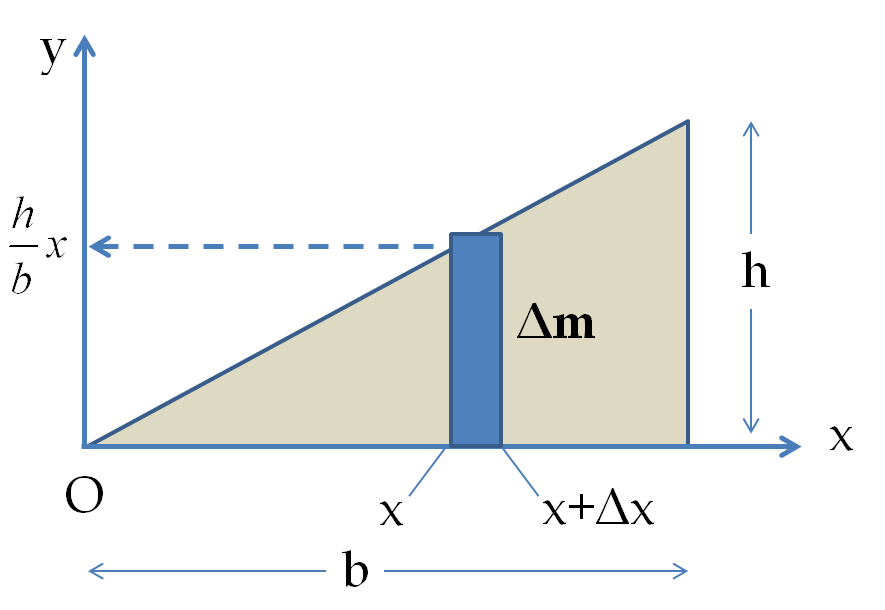
To locate the center of mass of a continuous body, it is a common practice to first discretize the body by conceptually “breaking” it up into small cells. Then each cell can be replaced with its mass \(\Delta m\) at the centers of the cells. This process converts the original continuous body into an equivalent system of point masses. Now, we use the procedure of CM for point masses to obtain the CM of the original body.
\begin{equation}
\vec R_{\textrm{cm}} = \frac{1}{M}\sum{\vec r\Delta m}\tag{7.34}
\end{equation}
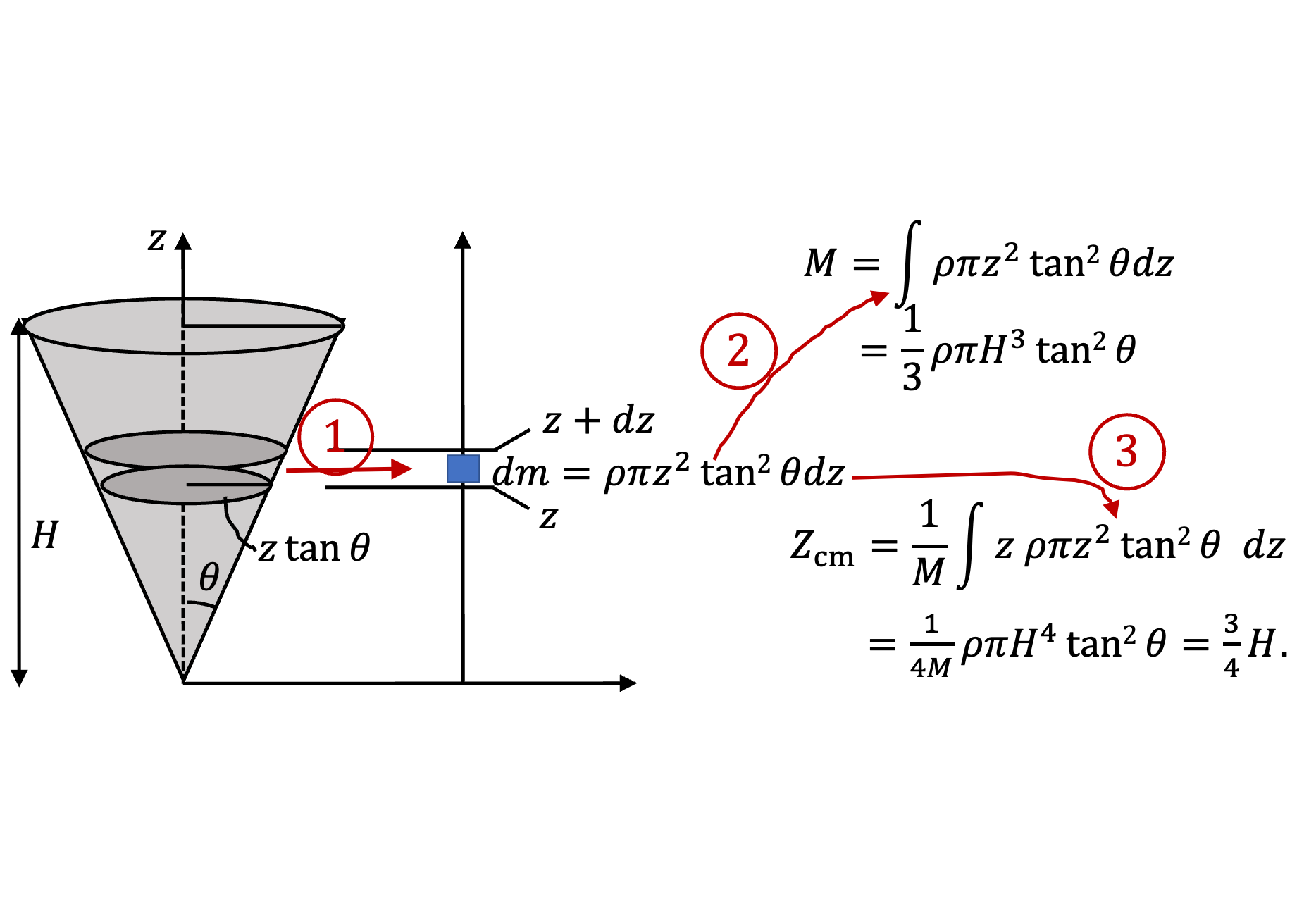
Let the volume of a cell be \(\Delta V\text{,}\) then the mass \(\Delta m\) will be
\begin{equation*}
\Delta m = \rho\Delta V.
\end{equation*}
Replacing
\(\Delta m\) in Eq.
(7.34) we obtain
\begin{equation}
\vec R_{\textrm{cm}} = \frac{1}{M}\sum{\vec r\rho\Delta V}\tag{7.35}
\end{equation}
In the limit of infinitesimally small cell sizes, the sum becomes an integral over the volume.
\begin{equation}
\vec R_{\textrm{cm}} = \frac{1}{M}\int{\vec r\rho dx dy dz},\tag{7.36}
\end{equation}
where the volume integration has been written using Cartesian coordinates. For a system with uniform density the density comes out of the integral.
\begin{equation}
\vec R_{\textrm{cm}} = \frac{\rho_0}{M}\int{\vec r dx dy dz}.\tag{7.37}
\end{equation}
For calculations, it is better to think of Eq.
(7.37) in terms of the components.
\begin{align*}
\amp X_{\textrm{cm}} = \frac{\rho_0}{M}\int{x dx dy dz}\\
\amp Y_{\textrm{cm}} = \frac{\rho_0}{M}\int{y dx dy dz}\\
\amp Z_{\textrm{cm}} = \frac{\rho_0}{M}\int{z dx dy dz}
\end{align*}
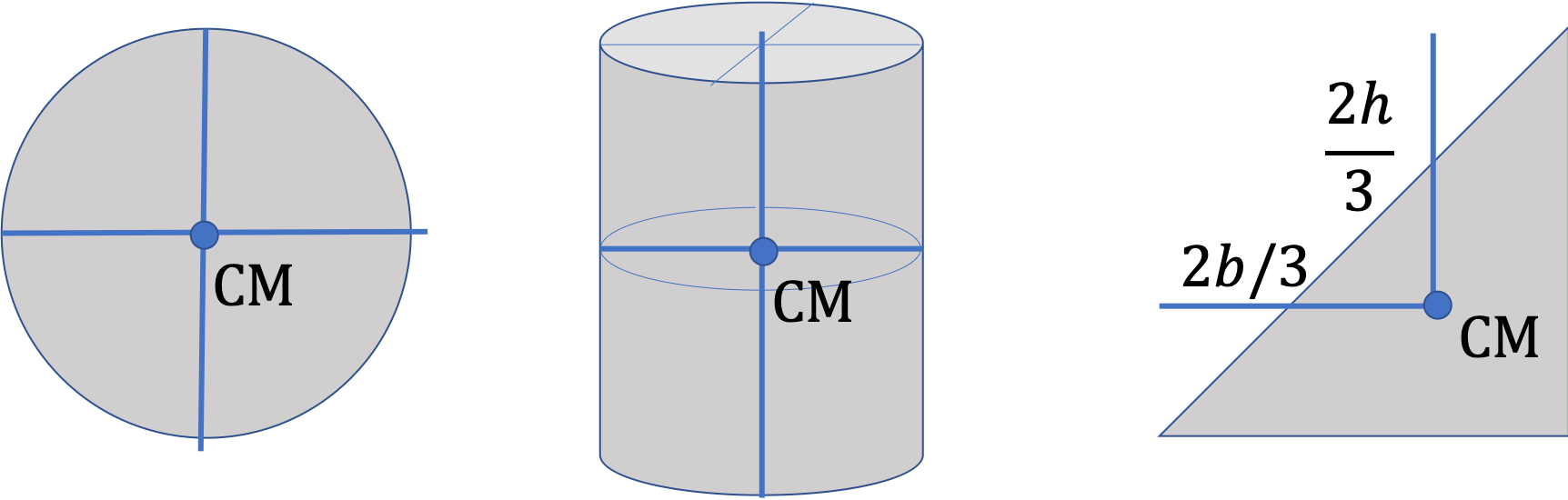
These are triple integrals for a body that occupies a three-dimensional space. These integrals simplify to one and two-dimensional integrals for rods and plates.