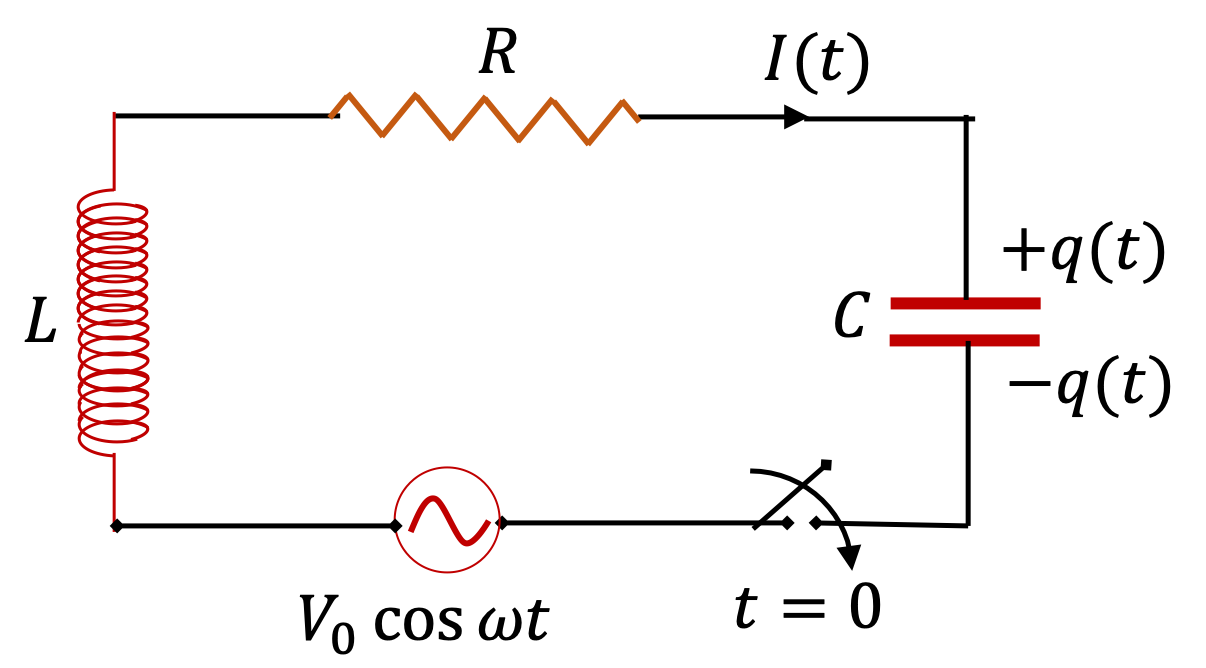
Example 41.30. Impedance, Current, and Voltages in an RLC circuit.
A \(20\text{-}\Omega\) resistor,\(50\text{-}\mu\text{F}\text{,}\) and \(30\text{-mH}\) inductor are connected in series with an AC source of amplitude \(10\text{ V}\) and frequency \(125\text{ Hz}\text{.}\)
- What is the (amplitude of) impedance of the circuit?
- What is the amplitude of the current in the circuit?
- What is the phase constant of the current? Is it leading or lagging the source voltage?
- Write voltage drops across resistor, inductor and capacitor, and the source voltage as a function of time.
Answer.
(a) \(20\ \Omega\text{,}\) (b) \(0.5\text{ A}\text{,}\) (c) \(5.4^{\circ}\text{,}\) (d) With \(V_{\text{Source}} = 10.0\ \text{V} \cos(250\pi t)\text{,}\) \(V_R = 9.96\ \text{V} \cos(250\pi t + 5.4^{\circ})\text{,}\) \(V_C = 12.7\ \text{V} \cos(250\pi t + 5.4^{\circ}-90^{\circ})\text{,}\) and \(V_L = 11.8\ \text{V} \cos(250\pi t + 5.4^{\circ}+90^{\circ})\text{.}\)
Solution 1. a
\(|Z| = \sqrt{R^2 + |X_L - X_C|^2} = 20.1\:\Omega
\text{.}\)
Solution 2. b
\(I_0 = \dfrac{V_0}{|Z|} \approx 0.5\:\text{A}\text{.}\)
Solution 3. c
We have \(X_L = 2\pi f L = 23.60\:\Omega\text{,}\) and \(X_C = 1/2\pi f C = 25.5\:\Omega\text{.}\) Since \(X_C \gt X_L\) the current will lead the EMF. The angle of lead will be
\begin{equation*}
\phi = \tan^{-1}\left(\dfrac{X_C - X_L}{R} \right) = 5.4^{\circ} = 0.095\:\text{rad}.
\end{equation*}
Solution 4. c
We found above the common current to be \(I = (0.5\:\text{A})\:\cos(2\pi\times 125\: t + 0.095)\text{.}\) Therefore, the voltage drops across various elements as a function of time will be
\begin{align*}
\amp V_R(t) = (0.5\:\text{A}\times R)\:\cos(2\pi\times 125\: t + 0.095)\\
\amp V_L(t) = (0.5\:\text{A}\times X_L)\:\cos\left(2\pi\times 125\: t + 0.095+\frac{\pi}{2}\right)\\
\amp V_C(t) = (0.5\:\text{A}\times X_C)\:\cos\left(2\pi\times 125\: t + 0.095-\frac{\pi}{2}\right)\\
\amp V(t) = (0.5\:\text{A}\times |Z|)\:\cos\left(2\pi\times 125\: t \right)
\end{align*}
Putting in the numerical values for \(R\text{,}\) \(X_L\text{,}\) \(X_C\) and \(|Z|\) gives
\begin{align*}
\amp V_R(t) = (10\:\text{V})\:\cos(250\pi \: t + 0.095)\\
\amp V_L(t) = (11.8\:\text{V})\:\cos\left(250\pi \: t + 0.095+\frac{\pi}{2}\right)\\
\amp V_C(t) = (12.75\:\text{V})\:\cos\left(250\pi \: t + 0.095-\frac{\pi}{2}\right)\\
\amp V(t) = (10\:\text{V})\:\cos\left(250\pi \: t \right)
\end{align*}