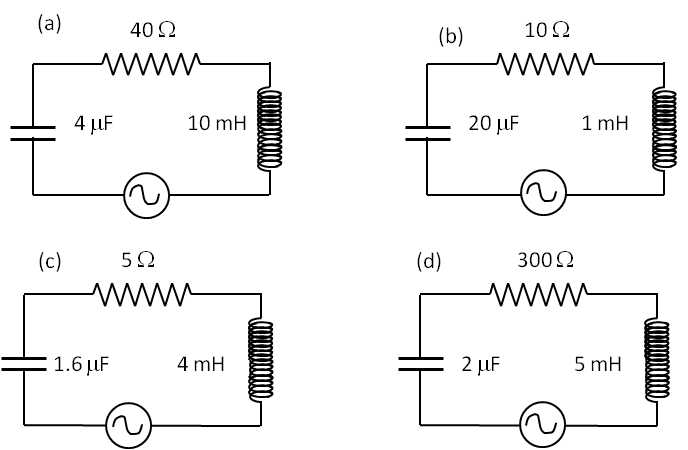
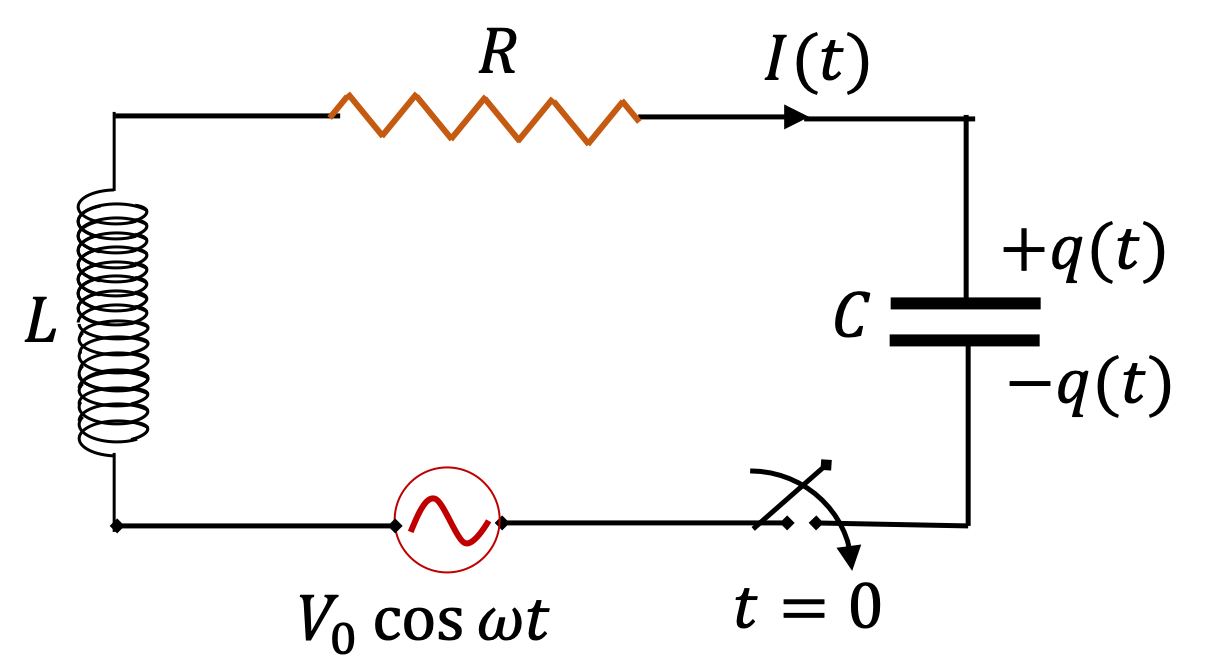
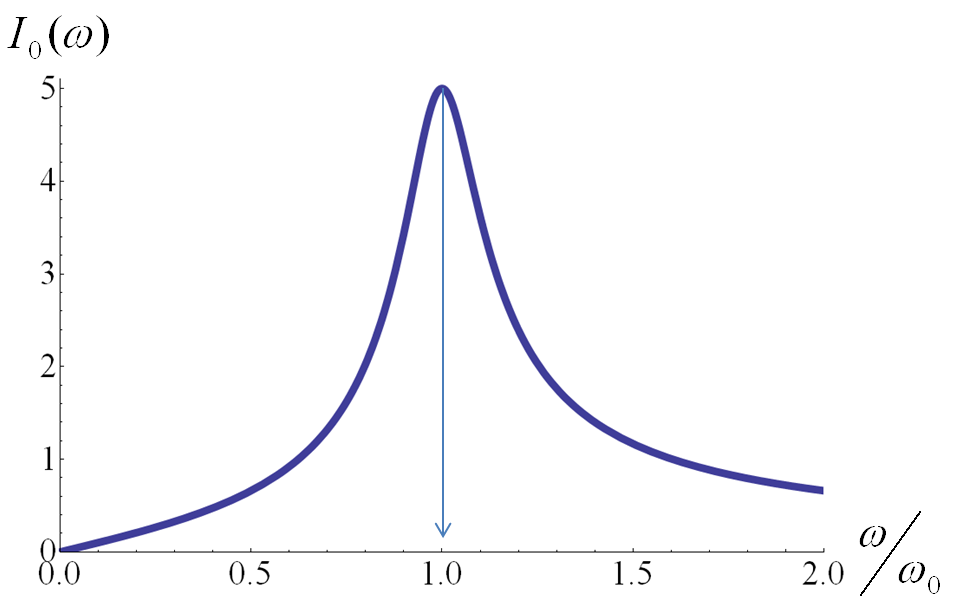
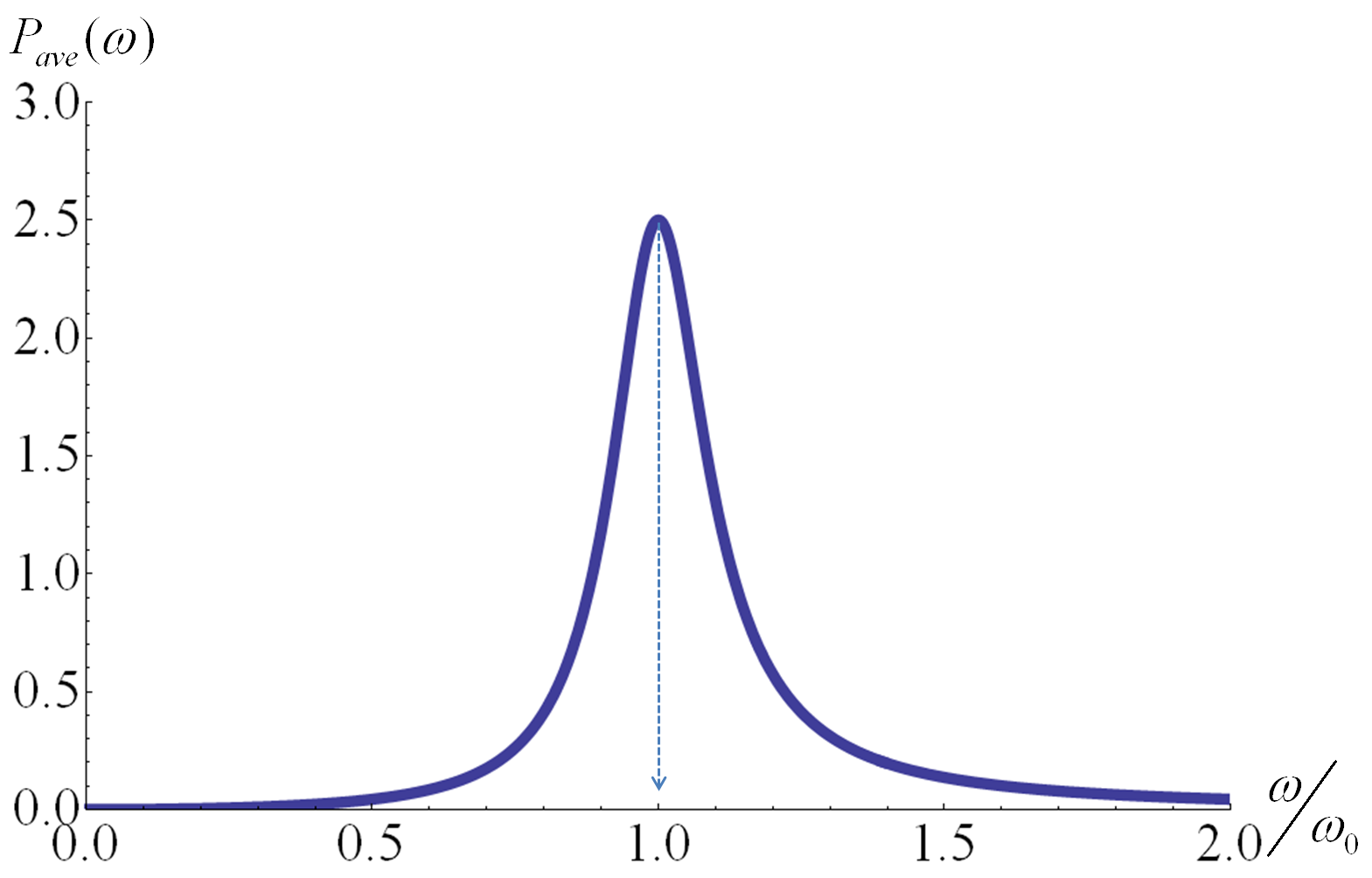
Eq.
(40.35) is an inhomogeneoud linear differential equation. Its solution has two parts, which we will denote by
\(q_c\) and
\(q_s\text{,}\) with the following exporesions for underdamped case, i.e., when
\(\gamma/2 \lt \omega_0\text{.}\)
\begin{equation}
q(t) = q_c(t) + q_s(t),\tag{40.36}
\end{equation}
with
\begin{align}
\amp q_c = e^{-\gamma t / 2} \left( A\, \cos \omega_1 t + B\, \cos \omega_1 t \right),\tag{40.37}\\
\amp q_s = q_\text{amp}\, \cos (\omega t + \phi_q),\tag{40.38}
\end{align}
where
\begin{equation}
q_\text{amp} = \dfrac{V_0/L}{ \sqrt{ (\omega^2 - \omega_0^2)^2 + \gamma^2 \omega^2 } },\tag{40.39}
\end{equation}
and,
\begin{equation}
\tan \phi_q = = \dfrac{ \gamma \omega }{\omega^2 - \omega_0^2 } = \dfrac{ 1 }{(\omega L/R) - (1/\omega RC) },\tag{40.40}
\end{equation}
and \(A\) and \(B\) are constants to be fixed using initial values of charge \(q\) and current \(I\text{.}\)
The voltage across the capacitor is of course given by the charge divided by the capacitance, i.e., \(V_c = Q/C\text{.}\) The steady state will oscillate with same frequency and phase as \(q\) above and with amplitude of voltage \(V_{c,0}\) will be
\begin{equation}
V_\text{0C} = \frac{q_\text{amp}}{C}.\tag{40.41}
\end{equation}
Current \(I\) in the circuit at arbitrary time is obtained by
\begin{equation*}
I = \dfrac{dq}{dt}.
\end{equation*}
In Eq.
(40.37), you can see that, with time, the multiplicative negative exponetial will make it negligible after
\(t \gt \gt 2/\gamma\text{.}\)
\begin{equation*}
q_c(t)\rightarrow 0 \text{ as } t\gt \gt 2/\gamma.
\end{equation*}
This leaves \(q_s\) part the only part, which is the steady state solution. We notice that \(q_s(t)\) is sinusoidal with same frequency as the driving EMF.
\begin{equation*}
q(t) \rightarrow q_s(t) \text{ as } t\gt \gt 2/\gamma.
\end{equation*}
By taking time derivative of \(q_s\) we get steady state current, \(I_s\text{.}\)
\begin{align*}
I_s \amp = \dfrac{dq_s}{dt} = -\omega q_\text{amp}\, \sin (\omega t + \phi_q), \\
\amp = \omega q_\text{amp}\, \cos (\omega t + \phi_q + \pi/2), \\
\amp = \omega I_0\, \cos (\omega t + \phi_I),
\end{align*}
where current amplitude,
\begin{align*}
I_0 \amp = \omega q_\text{amp} \\
\amp = \omega \dfrac{V_0/L}{ \sqrt{ (\omega^2 - \omega_0^2)^2 + \gamma^2 \omega^2 } } \\
\amp = \dfrac{V_0}{ \sqrt{ R^2 + \left(\omega L - \dfrac{1}{\omega C}\right)^2 } },
\end{align*}
and the phase constant,
\begin{align*}
\tan \phi_I \amp = \tan (\phi_q + \pi/2 )\\
\amp = -1.0/\tan \phi_q = \left( \dfrac{1}{\omega R C} - \dfrac{\omega L}{R}\right) .
\end{align*}