Mass Varying System

Section 7.9 Mass Varying System

There are many systems of interest in which the mass of the system is not constant in time. For instance, a rocket loses fuel when it is in the accelerating phase, a squid propels itself forward by ejecting water from back, etc. Although, in the case of rocket, for instance, the total mass of the rocket and the ejected fuel does not change, we are normally interested in describing the motion of the rocket only, which does lose the fuel and hence its mass changes with time. Similarly, when rain drops fall, they gather more water molecules thus increasing their mass with time. These systems are called syterms with time-varying mass or open systems.

In these examples object of interest accelerates even in the absence of an external force, apparently violating \(\vec F = m\vec a\text{.}\) The reason is that \(\vec F = m\vec a\) is not correct if \(m\) changes with time. We need the general form of second law of motion in terms of momentum, either in its differential form or integral form.

\begin{equation} \vec F = \frac{\Delta \vec p}{\Delta t} \rightarrow \dfrac{d\vec p}{dt}, \ \ \leftrightarrow\ \ \vec J = \int \vec F dt = \Delta \vec p .\tag{7.88} \end{equation}

Besides needing to work with \(\vec J = \Delta \vec p\) or \(\vec F = d\vec p/dt\text{,}\) there is also a question of what is included in the system and what is not. A good way to proceed is to look at how momentum changes in an infinitesimal interval of time \(\Delta t\text{.}\) We will work out examples to show this method below.

Subsection 7.9.1 Motion of a Rocket in Free Space

Consider a rocket far away from planets and stars so that we can focus exclusively on effects of changing mass. Let \(m(t)\) be the mass of the rocket and \(v_x(t)\) be its \(x\)-velocity at instant \(t\) with respect to a fixed frame as shown in Figure 7.93.

Figure 7.93. Rocket plus fuel at two closeby instants.

During interval \(t\) to \(t + \Delta t\text{,}\) burnt fuel of mass \(\Delta m\) is ejected from back. Let us assume that the ejected gas has speed \(u\) with respect to the rocket at instant \(t\text{.}\) The remainder of the rocket has mass \(m(t)-\Delta m\) and has \(x\)-velocity \(v_x + \Delta v_x\) with respect to the fixed frame.

The interval between \(t\) to \(t+\Delta t\) is just like one-dimensional explosion problems you have studied. To apply conservation of momentum with respect to the fixed frame, we will need to express all velocities with respect to the fixed frame. The \(x\)-velocity of the ejected fueld with respect to the fixed frame will be \(v_x -u\text{,}\) where \(u>0\) and negative sign results due to fuel moving towards negative \(x\)-axis.

The \(x\)-equation of conservation of momentum will be

\begin{equation*} m v_x = |\Delta m| ( v_x -u ) + ( m - |\Delta m| ) (v_x + \Delta v_x). \end{equation*}

Note that \(|\Delta m \Delta v_x| \ll |u\Delta m| \text{ or } | m\Delta v_x| \text{,}\) we drop \(\Delta m \Delta v_x\text{.}\) This gives the following relation.

\begin{equation*} m \Delta v_x = u |\Delta m|. \end{equation*}

Dividing by \(\Delta t\) we obtain the correct equation of motion for a rocket, which is sometimes called rocket equation.

\begin{equation*} m \frac{\Delta v_x}{\Delta t} = u \frac{|\Delta m|}{\Delta t}. \end{equation*}

Now, when we take \(\Delta t \rightarrow 0\) limit, we obtain the equation at instant \(t\) as a differential equation. Here, we need to observe that \(|\Delta m|/\Delta t\) should be positive but mass \(m(t)\) of the rocket is decreasing with time. So, \(|\Delta m|/\Delta t\) will go over to \(-dm/dt\) rather than \(dm/dt\text{.}\)

\begin{equation} m \frac{d v_x}{d t} = - u \frac{d m}{d t}.\tag{7.89} \end{equation}

Left side is \(m a_x\) of the rocket at instant \(t\) and right side is called the force of thrust provided by the ejecting burnt fuel. This equation can be solved by calculus to give the following expression for the final velocity \(v_f\text{,}\) when mass of the rocket has gone from \(m_i\) to \(m_f\text{.}\)

\begin{equation} v_{x,f} = v_{x,i} + u \ln\frac{m_i}{m_f}.\tag{7.90} \end{equation}

Remark 7.94.

We give the missing steps here. First we multiply both sides of Eq. (7.89) by \(dt/m\text{.}\) This gives

\begin{equation*} d v_x = - u \frac{d m}{m}. \end{equation*}

Now, integrating from \(t=t_i\) to \(t=t_f\) has limits \(v_{x,i}\,\text{to}\, v_{x,f}\) on the left side and the limits \(m_i\,\text{to}\, m_f\) on the right side.

\begin{equation*} \int_{v_{x,i}}^{v_{x,f}}d v_x = -\int_{m_i}^{m_f}u \frac{d m}{m}. \end{equation*}

Since \(dm/m = d(\ln\,m)\) and \(u\) is independent of \(m\text{,}\) we immediately get

\begin{equation*} v_{x,f} - v_{x,i} = - u \ln\frac{m_f}{m_i} = u \ln\frac{m_i}{m_f}. \end{equation*}

Subsection 7.9.2 Rocket Motion With Constant External Force

Rocket motion near the surface of the Earth surface is subject to approximately constant gravitational force of the Earth. In this subsection we examine the vertical component of the motion of the rocket near the Earth, for instance, when a rocket is launched as shown for the launch of the Zvezda service module of the International Space Station on a Russian Proton-K rocket. in Figure 7.95.

Figure 7.95. Photcredit: NASA/Wikicommons

Let the fuel be ejected at a constant speed \(u\) with respect to the rocket. We set up the problem in the same way as we did for the rocket in space, and add the force of gravity to the equation to obtain the following equation of motion of the \(y\)-coordinate of the rocket.

\begin{equation} m\ dv_y + u\ dm =-mgdt.\tag{7.91} \end{equation}

Dividing this equation by \(m\) and combining \(dv_y\) and \(dt\) terms we obtain a simpler form.

\begin{equation} d\left(v_y+gt\right) + \frac{u}{m}\ dm=0.\tag{7.92} \end{equation}

Let us write

\begin{equation*} w \equiv v_y+gt, \end{equation*}

so that Eq. (7.92) looks simpler.

\begin{equation} dw + \frac{u}{m}\ dm=0.\tag{7.93} \end{equation}

We integrate this equation from \(t=0\) to \(t=t\) to obtain

\begin{equation} w(t)-w(0)= u\ln\left(\frac{M}{m(t)}\right),\tag{7.94} \end{equation}

where \(M\) is the mass of the rocket at \(t=0\text{.}\) Putting the velocity back in we get

\begin{equation} v_y(t)-v_{y0}= - gt + u\ln\left(\frac{M}{m(t)}\right).\tag{7.95} \end{equation}

For a constant burn rate \(\alpha\text{,}\) we replace \(m(t)\) by \(M-\alpha t\) to obtain the following for the \(y\)-component of the velocity.

\begin{equation} v_y(t)-v_{y0}= - gt + u\ln\left(\frac{M}{M-\alpha t}\right), \ \ 0\le t \le t_f,\tag{7.96} \end{equation}

where \(t_f = (M-M_R)/\alpha\) is the time when the rocket runs out of fuel and left with the rocket body only with mass \(M_R\text{.}\)

Subsection 7.9.3 Example of Mass Accretion

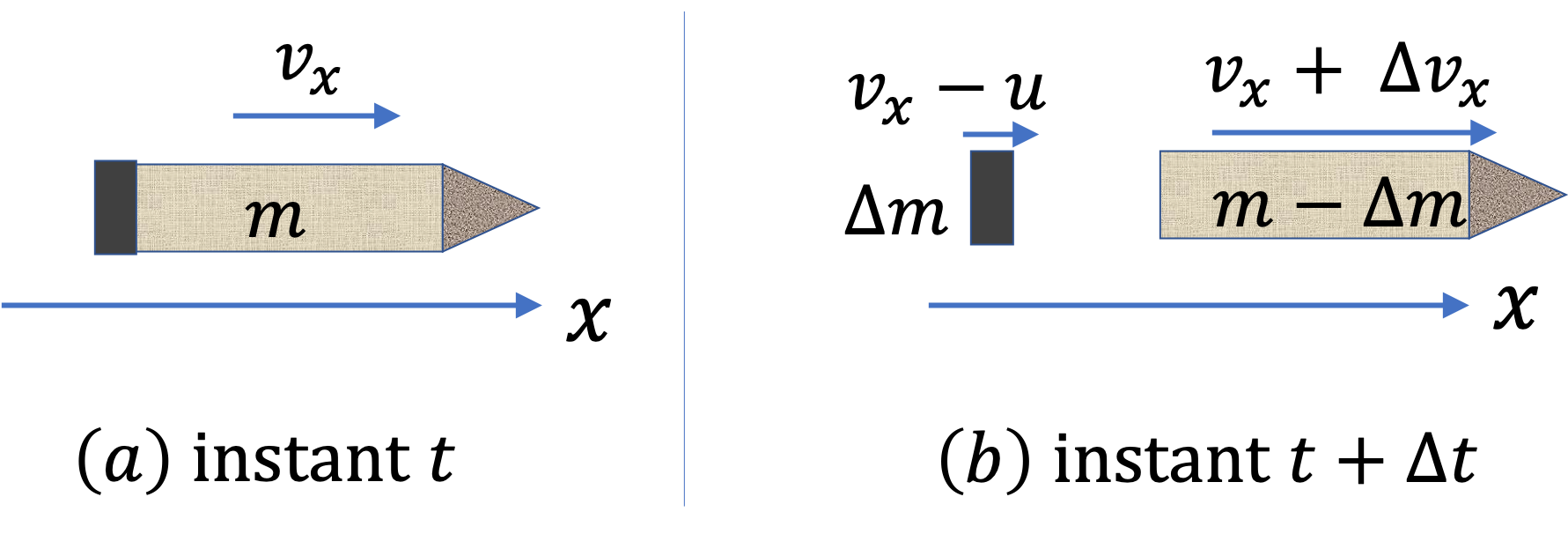
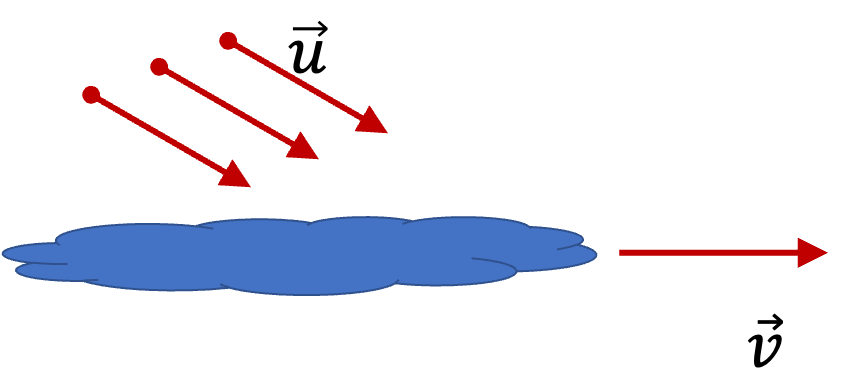
Rocket motion is an example where the object of interest is losing mass in time, which led to the crucial minus sign when we went from \(|\Delta m|/\Delta t\) to \(-dm/dt\text{.}\) We now look at a situation in which the object of interest gains mass with time.

Consider a spaceship moving in space where it is struck by a continuous stream of particles which stick to the ship.

Let \(m(t)\) and \(\vec v(t)\) be the mass and velocity of the spaceship at instant \(t\text{.}\) Let particles move with velocity \(\vec u\) and add a mass \(\Delta m\) to the spaceship in duration from \(t\) to \(t + \Delta t\text{.}\)

Let \(\vec v' = \vec v + \Delta \vec v\) be the velocity of the spacecraft at \(t+\Delta t\text{.}\) Then, change in momentum in this duration will be

\begin{equation*} \Delta \vec p = (m+\Delta m)\, \vec v' - (m\, \vec v + \Delta m\, \vec u). \end{equation*}

Simplifying we have

\begin{equation*} \Delta \vec p = m\, \Delta \vec v + \Delta m\, ( \vec v - \vec u ) + \Delta m \Delta \vec v. \end{equation*}

Dividing by \(\Delta t\) we get

\begin{equation*} \frac{\Delta \vec p}{\Delta t} = m\, \frac{\Delta \vec v}{\Delta t} + \frac{\Delta m}{\Delta t}\, ( \vec v - \vec u ) + \Delta m \frac{\Delta \vec v}{\Delta t}. \end{equation*}

(Calculus Part) Taking \(\Delta t \rightarrow 0\) limit will mean \(\Delta m \rightarrow 0\) and \(\Delta v\rightarrow 0\) as well. In this limit we see that the last term drops out and the other terms turn into derivatives.

\begin{equation*} \frac{d\vec p}{dt} = m\, \frac{d \vec v}{dt} + \frac{d m}{d t}\, ( \vec v - \vec u ). \end{equation*}

Let \(\vec F\) be the net external force on the spaceship. By, \(\vec F = d\vec p/dt\text{,}\) we must have

\begin{equation} \vec F = m\, \frac{d \vec v}{d t} + \frac{d m}{d t}\, ( \vec v - \vec u ).\tag{7.97} \end{equation}

In the absence of any force \(\vec F=0\text{,}\) the velocity of the spaceship will change according to

\begin{equation*} m\, \frac{d \vec v}{d t} = - \frac{d m}{d t}\, ( \vec v - \vec u ), \end{equation*}

which is usullay analyzed in component form, e.g., for \(x\)-component we will get the following (and similarly for other components).

\begin{equation} \frac{dv_x}{ v_x - u_x} = - \frac{dm}{m}.\tag{7.98} \end{equation}

Equation (7.97) also says that if you wanted the velocity of the spaceship steady at \(\vec v\text{,}\) i.e., you required \(d \vec v/dt = 0\text{,}\) you will need a force, e.g., by rockets on the ship, of the magnitude and direction given by

\begin{equation*} \vec F = \frac{d m}{d t}\, ( \vec v - \vec u ). \end{equation*}

This equation is consistent with the observation that if \(\vec u = \vec v\text{,}\) particles will move at the same velocity as the ship and hence will never strike the ship. In that case ship does not need any force to act on it to maintain constant velocity.

Subsection 7.9.4 Momentum Transport by Massless Radiation

Light particles, called photons, do not have mass but carry momentum and energy. The formula for the magnitude of momentum for a photon in light of wavelength \(\lambda\) is given by

\begin{equation} p = \frac{h}{\lambda},\tag{7.99} \end{equation}

where \(h\) is called Planck’s constant and has the following value.

\begin{equation*} h = 6.626 \times 10^{-34}\, \text{m}^2\text{kg/s}. \end{equation*}

An example of application of momentum from photons, consider a payload that uses large solar sail to collect momentum from photons from the star for its navigation. Suppose area of the sail is \(A\text{.}\) Let intensity of radiation from the star be such that \(N\) photons of wavelength \(\lambda\) per unit volume are traveling in the direction of the payload.

Since speed of light in space will be equal to \(c=3\times 10^{8}\,\text{m/s}\text{,}\) the number of photons striking the collector in time \(\Delta t\) will be

\begin{equation*} \Delta n = N A c. \end{equation*}

For the sake of simplicity, let us suppose that momentum of photon flips in direction upon reflection. That will mean that each photon will increase the momentum of the payload by twice its own momentum.

\begin{equation*} \Delta p_\text{payload} = 2 N A c h /\lambda \Delta t. \end{equation*}

Now, let us look at some numbers to get a sense of the size of the effect. Consider visible light photon of wavelength \(0.5\,\mu\text{m}\text{,}\) area \(A=50\text{ m}^2\text{,}\) number density \(N=10^{12}\text{ m}^{-3}\text{.}\) This will impose following force on the payload.

\begin{align*} F \amp = \Delta p_\text{payload}/\Delta t\\ \amp = 2\times 10^{12}\times 50\times3\times 10^8\times 6.626\times10^{-34}/(0.5\times 10^{-6})\\ \amp = 4.0\times 10^{-5}\text{ N}. \end{align*}

This is not too small to ignore.

Exercises 7.9.5 Exercises

1. Rocket Acceleration at Constant Burn Rate.

A spacecraft is moving at a constant speed of \(100\text{ m/s}\) in gravity-free space along a straight path. The crew decided to accelerate the spacecraft. When the pilot turns on one of the thrusters, it ejects burnt fuel in the back at the rate of \(10.0 \text{ kg/s}\) at a speed of \(1,000\text{ m/s}\) relative to the craft. At the moment the thruster was turned on, the mass of the spacecraft with crew plus the unburnt fuel was \(5.0\times 10^{5}\text{ kg}\text{.}\)

(a) What is the thrust on the spacecraft?

(b) Express the acceleration of the craft as a function of time, \(t \text{,}\) and evaluate the acceleration at the following values \(t \) : (i) \(0 \text{,}\) (ii) \(10\text{ s} \text{,}\) (iii) \(100\text{ s}\text{,}\) where \(t=0 \) is the instant when the thruster was turned on:

(c) Find the speed of the spacecraft as a function of time, and evaluate the speed at the following values \(t \) : (i) \(0 \text{,}\) (ii) \(100\text{ s} \text{,}\) (iii) \(10000\text{ s}\text{.}\)

Hint.

Use the formulas.

Answer.

(a) \(10,000\text{ N} \text{,}\) (b) \(0.02\text{ m/s}^2\text{,}\) \(0.02004\text{ m/s}^2\text{,}\) \(0.025\text{ m/s}^2\text{,}\) (c) Not provided.

Solution 1. (a)

(a) The thrust \(T \) on the spacecraft comes from the rate at which mass is lost and the velocity of that ejected mass.

\begin{equation*} T = \alpha u = 10.0 \text{ kg/s} \times 1,000\text{ m/s} = 10,000\text{ N}. \end{equation*}

The direction of the thrust is towards forward of the spacecraft since the burnt fuel is being ejected in the backward direction.

Solution 2. (b)

(b) Using the full Newton’s equation equation with no external force:

\begin{equation*} m\vec a = \vec T, \end{equation*}

where mass \(m \) is decreasing with time with the following value at instant \(t \text{.}\)

\begin{equation*} m = m_0 - \alpha\, t, \end{equation*}

where

\begin{equation*} m_0 = 5.0\times 10^{5}\text{ kg} ,\ \ \alpha = 10.0 \text{ kg/s}. \end{equation*}

Let \(x \) axis be pointed in the forward direction. Then, we have the following for the \(x\) component of acceleration at instant \(t\text{.}\)

\begin{equation*} a_x = \dfrac{T_x}{m} = \dfrac{T}{m_0 - \alpha\, t}. \end{equation*}

Therefore, magnitude \(a \) of acceleration is

\begin{equation*} a(t) = \dfrac{10,000}{5\times 10^5 - 10\, t}. \end{equation*}

(i)

\begin{equation*} a(0) = \dfrac{10,000}{5\times 10^5 } = 0.02\text{ m/s}^2 \end{equation*}

(ii)

\begin{equation*} a(100\text{ s}) = \dfrac{10,000}{5\times 10^5 - 1\times 10^3} = 0.02004\text{ m/s}^2 \end{equation*}

(ii)

\begin{equation*} a(10^4\text{ s}) = \dfrac{10,000}{5\times 10^5 - 1\times 10^5} = 0.025\text{ m/s}^2 \end{equation*}

Solution 3. (c)

\begin{equation*} v = v_0 + u \ln\left( \dfrac{m_0}{m_0-\alpha t}\right). \end{equation*}

2. Grain Filling a Uniformly Moving Cart.

A cart of mass \(M\) is moving at a constant velocity \(v\) as shown. When the cart enters the space below a large funnel, grain starts to fill the cart at constant mass rate, \(\Delta m/\Delta t =\alpha\text{.}\)

In order to keep the track moving at constant velocity, you need to constantly apply a force \(F\text{.}\) Find an expression of this force.

Hint.

Use \(\vec F\Delta t = \Delta \vec p\) in a duration \(\Delta t\text{.}\)

Answer.

\(\alpha v\text{.}\)

Solution.

Consider a interval from \(t\) to \(t+\Delta t\) when the mass of grain and cart goes from \(m\) to \(m + \alpha \Delta t\text{.}\) Let \(x\)-axis be pointed in the direction of constant velocity. Using \(J_x = \Delta p_x\text{,}\) we will get

\begin{equation*} F\Delta t = (m + \alpha \Delta t)\, v - m v= \alpha \Delta t)\, v. \end{equation*}

Therefore, \(F = \alpha v\text{.}\)

3. A Monkey Land in a Moving Crate and Starts to Consume Bananas.

A crate of mass \(50\) kg containing bananas is sliding in a straight line on a frictionless surface at a constant velocity of \(10\) m/s horizontally. A monkey of mass \(45\) kg hanging from the ceiling times it correctly and jumps vertically down landing in the crate. At the time monkey lands in the crate his velocity was \(12\) m/s vertically downward.

What is the velocity of the crate with monkey afterwards?
Compare the momenta of the crate plus monkey afterwards to that of the crate plus the monkey separately. Is the total momentum of the crate plus monkey system conserved? Why or why not?
After landing, the monkey starts to consume banana and throws away the peels each having mass of \(200\)-grams at a constant rate of one banana per \(40\) seconds and a speed of \(5\) m/s with respect to the crate. The peels are being thrown in the forward direction of the motion of the cart. If there are \(100\) bananas, what will be the final velocity of the monkey and crate?

Solution 1. a

Let the horizontal direction in which the crate moves be the positive \(x\)-axis and vertically up direction be the positive \(y\)-axis. Then, the crate has \(p_x\) and the monkey \(p_y\) before the monkey lands. After the monkey lands, the vertical \(p_y\) of the monkey goes to zero as a result of vertically force from the ground. The only component that is conserved in this process is the \(x\)-component of momentum.

\begin{equation*} p_x(\textrm{of crate}) = p_x(\textrm{of crate and monkey together}). \end{equation*}

Putting in the numbers we get

\begin{equation*} 50\ \textrm{kg}\times 10\ \textrm{m/s} = (50\ \textrm{kg} + 45\ \textrm{kg}) v\ \ \Longrightarrow \ \ v = 5.3 \ \textrm{m/s}. \end{equation*}

The velocity has the same direction as the direction of the velocity of the crate before the monkey jumped in the crate.

Solution 2. b

The momentum of the monkey plus crate has both horizontal and vertical components before monkey hits the crate in its fall, but afterwards the two together have only the horizontal component. The momentum is not conserved since there are external forces, here the normal force, in the vertical direction whose impulse is not zero.

Solution 3. c

Let \(M\) be the mass of the monkey and crate and \(Nm_b\) be the mass of the \(N\) bananas in the crate. Let \(v_j\) be the \(x\)-component of the crate with monkey and rest of the banana when \(j\) bananas have been thrown. Let \(u\) be the \(x\)-component of the velocity of the banana with respect to the crate. The \(x\)-component of the velocity of the banana will be \((v_j-u)\text{.}\) The conservation of momentum in the \(j\)-th step will give

\begin{equation*} \left[ M + (N-j) m_b \right] v_j +m_b (v_j-u)= \left[ M + (N-j+1) m_b \right] v_j \end{equation*}

This equation can be solved to find \(v_j - v_{j-1}\text{.}\)

\begin{equation*} v_j = v_{j-1} + \left[ \frac{m_b}{M + (N-j+1) m_b} \right]\ u \end{equation*}

Summing the equations for \(v_1\text{,}\) \(v_2\text{,}\) \(\cdots\text{,}\) \(v_N\) gives

\begin{equation*} v_N = v_0 + m_b u\ \sum_{j=1}^{N} \left[ \frac{1}{M + (N-j+1) m_b} \right]. \end{equation*}

I leave for the student to play with the numerical values given.

4. (Calculus) Rocket Motion Moving Opposite to Gravity.

Rocket motion near the surface of the Earth is subject to an approximately constant gravitational force of the Earth.

Consider a rocket of initial total mass \(M_0 \) with \(M_r \) the mass of the rocket without the fuel. The rocket is rising straight up near Earth with the fuel being ejected at a constant speed \(u\) with respect to the rocket and at a constant rate \(\alpha \text{ kg/s}\text{.}\)

Prove that the vertical component of the velocity at time \(t \) will be

\begin{equation*} v = v_0 - gt + u\ln\left(\frac{M_0}{M_0-\alpha t}\right) \end{equation*}

Hint.

Set up equation similar to the example with no external force.

Answer.

Already given in the statement.

Solution.

We will work with positive \(y\) axis pointed up. Let \(v_y \) denote \(y \) component of the velocity of the rocket at instant \(t \) and let \(\Delta v_y \) be the change in it during an interval between \(t \) and \(t + \Delta t \text{.}\) Notice also that velocity of the ejected fuel with respect to the inertial frame will be \(v_y - u\text{.}\)

Therefore, the change in momentum of the rocket plus burnt fuel combined system along the \(y \) axis is

\begin{align*} \Delta p_y \amp = \left[ \Delta m ( v_y - u ) + (m - \Delta m) (v_y + \Delta v_y ) \right] - m v_y,\\ \amp \rightarrow - u \Delta m + m \Delta v_y \text{ (as } \Delta t \rightarrow 0\text{.)} \end{align*}

The impulse of the external force of gravity on the rocket during the intreval is

\begin{equation*} J_y = - m(t) g \Delta t. \end{equation*}

Using the momentum-impulse relation we get

\begin{equation*} m \Delta v_y - u \Delta m = - m g \Delta t. \end{equation*}

Divide both sides by \(m\text{.}\) Now, taking the infinitesimal limit, the change \(\Delta v_x \) is replaced by \(dv_x \) and the change in mass \(\Delta m \) is replaced by \(-dm \) since \(dm \) is negative. We also write \(dm/m \) as \(d\ln m\text{.}\)

\begin{equation*} d v_y + u\, d \ln m = - g\, dt. \end{equation*}

Integrating from \(t = 0\) to \(t = t\) we find

\begin{equation*} v_y(t) - v_y(0) + u\,\ln\left(\frac{M_0-\alpha t}{M_0}\right) = - gt. \end{equation*}

In this equation we can write \(v_y(t) \) as \(v\) and \(v_y(0) \) as \(v_0\text{,}\) and rerarrange to get the desired result.

\begin{equation*} v = v_0 - gt + u\,\ln\left(\frac{M_0}{M_0-\alpha t}\right). \end{equation*}

Prev Top Next