Principal Axes

Section 10.3 Principal Axes

From the matrix representation of \({\bf I}\) in Eq. (10.13), it is obvious that it is a symmetric matrix. We say that moment of inertia is a symmetric tensor. Since symmetric matrices can always be diagonalized, there is a choice of direction of the body-attached axes so that off-diagonal elements turn out to be zero. We call these axes principal axes. In principal axes we will have only three non-zero moment of inertia components; in that case, we just denote them by simpler symbols, \(I_1\text{,}\) \(I_2\text{,}\) \(I_3\text{.}\)

\begin{equation*} {\bf I} = \begin{pmatrix} I_1 \amp 0 \amp 0\\ 0 \amp I_2 \amp 0\\ 0 \amp 0 \amp I_3 \end{pmatrix} \end{equation*}

Denoting \(x,y,z\) by \(x_1,\,x_2,\,x_3\) for simplicity and subscripts by simply \(1,\,2,\,3\) instead of \(x,y,z\text{,}\) we have

\begin{equation*} I_1 = \sum m (x_2^2 + x_3^2),\ \ I_2 = \sum m (x_1^2 + x_3^2),\ \ I_3 = \sum m (x_1^2 + x_2^2). \end{equation*}

From these, it is easy to see that sum of two of these moments of inertia cannot exceed the third.

\begin{equation*} I_1 + I_2 = \sum m (x_1^2 + x_2^2 + 2x_3^2) \ge \sum m (x_1^2 + x_2^2) = I_3. \end{equation*}

Based on the values of \(I_1,\ I_2,\ I_3\) we can classify systems into three categories: (1) if \(I_1=I_2=I_3\text{,}\) then we have spherical top, (2) if \(I_1 = I_2 \ne I_3\text{,}\) then we have symmetrical top, and (3) if all \(I_i\) are diferent, then we have asymmetrical top. Often, we work with systems that are elongated along one dimension, such as rod or linear molecules. In that case, we will have \(I_1=I_2\) and \(I_3=0\text{.}\) This type of system is called a rotator.

If there are symmetries in a rigid body, it is much simpler to guess the directions of principal axes. For instance, in the case of sphere, every axis through the CM is a principal axis.

In the case of a cylinder, one prinicipal axis will be the axis of the cylinder and the other two will be axes perpendicular to the axis of the cylinder and passing through the CM. In this case, we will get \(I_1=I_2\) and \(I_3\text{.}\)

A calculation on a cylinder of mass \(M\text{,}\) height \(H\) and radius \(R\) will show that moment of inertia tensor with respect to principal axes will be

\begin{equation*} {\bf I} = \begin{pmatrix} \frac{1}{4}MR^2 + \frac{1}{12}MH^2 \amp 0 \amp 0\\ 0 \amp \frac{1}{4}MR^2 + \frac{1}{12}MH^2 \amp 0\\ 0 \amp 0 \amp \frac{1}{2}MR^2 \end{pmatrix} \end{equation*}

When masses are restricted to be in a plane, we call it a coplanar system. For a coplanar system, say in the \(xy\) plane, let \(I_{1}\) and \(I_2\) be moments of inertia about principal axes in \(xy\)-plane and \(I_3\) be about principal axis perpendicular to the plane.

Since \(z=0\) for all particles in this system, we have

\begin{equation*} I_1 = \sum m y^2,\ \ I_2 = \sum m x^2,\ \ I_3 = \sum m (x^2 + y^2). \end{equation*}

Clearly, for coplanar systems we must have

\begin{equation*} I_3 = I_1 + I_2. \end{equation*}

Example 10.25. Moment of Inertia of a Dumbbell.

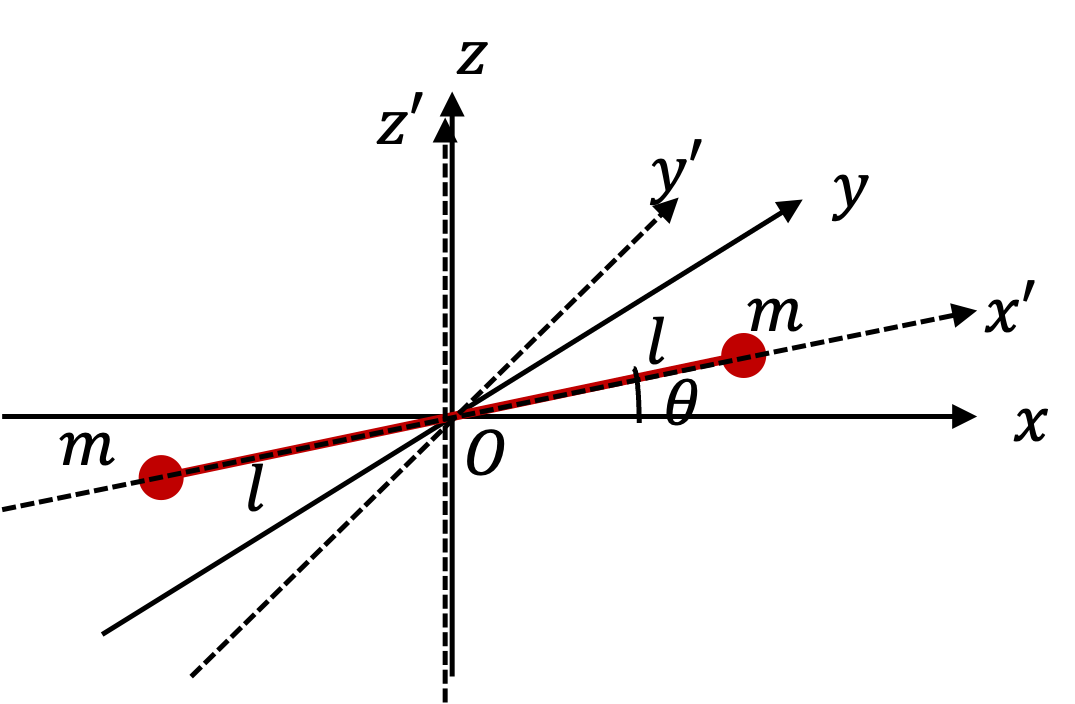
We want to find moment of inertia of a dumbbell with respect to two different coordinate systems shown in Figure 10.26. Find all nine moments of inertia in \(Oxyz\) and \(Ox'y'z'\text{.}\)

Answer.

See solution.

Solution.

We need coordinates of the two masses in the two systems. From Figure 10.26, we read off the following for the mass (say 1) on the right.

\begin{gather*} x_1 = l\cos\theta,\ \ y_1 = l \sin\theta,\ \ z_1 = 0\\ x'_1 = l,\ \ y'_1 = 0,\ \ z'_1 = 0 \end{gather*}

The coordinates of the other particle are negative of these values. Therefore, we get the following moments of inertia in \(Oxyz\text{.}\)

\begin{align*} \amp I_{xx} = 2m l^2 \sin^2\theta,\ \ I_{yy} = 2m l^2 \cos^2\theta,\ \ I_{zz} = 2m l^2,\\ \amp I_{xy} = -2m l^2 \sin\theta\,\cos\theta,\ \ I_{xz} = 0,\ \ I_{yz} = 0. \end{align*}

Organizing this in matrix we have the following in \(Oxyz\text{.}\)

\begin{equation*} {\bf I} = \begin{pmatrix} 2m l^2 \sin^2\theta \amp -2m l^2 \sin\theta\,\cos\theta \amp 0\\ -2m l^2 \sin\theta\,\cos\theta \amp 2m l^2 \cos^2\theta \amp 0\\ 0 \amp 0 \amp 2m l^2 \end{pmatrix} \end{equation*}

In \(Ox'y'z'\text{,}\) we will get

\begin{align*} \amp I_{x'x'} = 0,\ \ I_{y'y'} = 2m l^2,\ \ I_{z'z'} = 2m l^2,\\ \amp I_{x'y'} = 0,\ \ I_{x'z'} = 0,\ \ I_{y'z'} = 0. \end{align*}

Organizing this in matrix we have the following in \(Ox'y'z'\text{.}\)

\begin{equation*} {\bf I'} = \begin{pmatrix} 0 \amp 0 \amp 0\\ 0 \amp 2m l^2 \amp 0\\ 0 \amp 0 \amp 2m l^2 \end{pmatrix} \end{equation*}

Example 10.27. Principal Moments of Inertia of a Cone.

Find principal moments of inertia of a circular-based cone with radius \(R\) and height \(h\text{.}\)

Answer.

\(I_1 = I_2 = \frac{3}{20}\,MR^2 + \frac{3}{80}\,Mh^2\text{,}\) \(\frac{3}{10}\,MR^2\text{.}\)

Solution.

To find the principal moments of inertia about the CM at \(O\text{,}\) we first find moment of inertia about the apex at \(O'\) using axes parallel to the principal axes, and then make use of parallel axis theorem as illustrated in Figure 10.28 . We also make use of cylindrical coordinates since integrals will work out more easily there.

An element of mass \(dm = \rho\,dV\) at coordinates \((x',y',z')\) here will be

\begin{equation*} dm = \rho r'dr' d\phi' dz', \end{equation*}

where upper limit of integration on radial distance \(r' = \sqrt{ {x'}^2 + {y'}^2 }\) depends on \(z'\) from the ratio of sides of similar triangles,

\begin{equation*} \frac{r'_\text{max}}{z'} = \frac{R}{h},\ \ \longrightarrow\ \ r'_\text{max} = \frac{R}{h}\, z'. \end{equation*}

Mass of the cone will be

\begin{align*} M \amp = 2\pi \rho \int_0^h dz'\, \int_0^{r'_\text{max}}\, r'dr'\\ \amp = \frac{2\pi \rho R^2}{2 h^2} \int_0^h\, z'\, dz' = \frac{\pi R^2 h}{3}\, \rho. \end{align*}

To find \(I_{z'z'}\) we need

\begin{align*} I_{z'z'} \amp = \int \rho \left(x^2 + y^2 \right) dV \\ \amp = \rho \int {r'}^2 r'dr' d\phi' dz' \\ \amp = \frac{ 2\pi R^4 \rho}{4h^4} \int_0^h {z'}^4 dz' \\ \amp = \frac{ \pi R^4 h \rho}{10} = \frac{3}{10}\,MR^2. \end{align*}

For \(I_{x'x'}=I_{y'y'}\text{,}\) we need only one calculation.

\begin{align*} I_{x'x'} \amp = \int \rho \left(y^2 + z^2 \right) dV \\ \amp = \rho \int dz'\int r' dr'\, \int d\phi' \left( {r'}^2 \sin^2\phi' + {z'}^2\right) \\ \amp = \rho \int dz'\int r' dr'\, \left( \pi {r'}^2 + 2\pi {z'}^2\right) \\ \amp = \rho \int dz' \left( \frac{\pi}{4}{Rz'/h}^4 + \pi {Rz'/h}^2 {z'}^2\right) \\ \amp = \rho \left( \frac{\pi}{20}(R/h)^4 h^5 + \frac{1}{5}\,\pi (R/h)^2 h^5\right) \\ \amp = \frac{\pi\rho R^2 h}{3} \left( \frac{3}{20} R^2 + \frac{3}{5}h^2 \right) \\ \amp = \frac{3}{5}\,M \left( \frac{1}{4} R^2 + h^2 \right) \end{align*}

To make use of parallel axis theorem to get \(I_{xx}\text{,}\) \(I_{yy}\text{,}\) \(I_{zz}\) through the CM, we need to locate the CM of the cone. We just need to find the \(z'_\text{cm}\text{.}\) This will be at

\begin{equation*} z'_\text{cm} = \frac{1}{M}\int z' dV = \frac{3}{4}\, h. \end{equation*}

Now, we use parallel axis theorem to get

\begin{align*} I_{xx} \amp = I_{x'x'} - M {z'}_\text{cm}^2 = \frac{3}{5}\,M \left( \frac{1}{4} R^2 + h^2 \right) - \frac{9}{16} h^2 \\ \amp = \frac{3}{20}\,MR^2 + \frac{3}{80}\,Mh^2.\\ I_{yy} \amp = I_{xx} = \frac{3}{20}\,MR^2 + \frac{3}{80}\,Mh^2. \\ I_{zz} \amp = \frac{3}{10}\,MR^2. \end{align*}

Subsection 10.3.1 Parallel Axis Theorem

Often we want moment of inertia about an axis that does not pass through center of mass. We have seen this before, for instance, in the case of moment of inertia of a rod about an axis through the edge.

Given moment of inertia \(I_{1}=\frac{1}{12}ML^2\) about axis \(1\) through the center of the rod, the moment of inertia about an axis \(1'\) through the edge and parallel to the axis through the CM was

\begin{equation*} I_{1'} = I_{1} + Ma^2 = \frac{1}{3}ML^2. \end{equation*}

We want to generalize it. Suppose we have \(I_1,\, I_2,\ I_3\) are moments of inertial about principal axes \(1,\, 2,\ 3\) respectively, origin \(O\) at CM. Let there be axes \(1',\, 2',\ 3'\) that are parallel to \(1,\, 2,\ 3\) but with origin at \(A\) in the body such that the displacment from \(O\) to \(A\) be \(\vec a\text{.}\)

Consider a point P in the body. Let \(\vec r\) be its position with respect to \(O\) and \(\vec r'\) with respect to \(A\text{.}\) Then

\begin{equation*} \vec r = \vec r' + \vec a. \end{equation*}

The diagonal components of the moment of inertia will become

\begin{align*} I_{x'x'} \amp = \sum m (y'^2 + z'^2) \\ \amp \sum m [(y-a_y)^2 + (z-a_z)^2] \\ \amp \sum m (y^2 + z^2) + \sum m (a_y^2 + a_z^2) -2a_y\sum m y - 2a_z\sum m z \end{align*}

Last two terms here will be zero since \(O\) is at the CM, i.e, since \(\sum m \vec r = 0\text{,}\) we will end up with

\begin{equation*} I_{x'x'} = \sum m (y^2 + z^2) + \sum m (a_y^2 + a_z^2) = I_{xx} + \sum m (a_y^2 + a_z^2). \end{equation*}

Similarly for \(I_{y'y'}\) and \(I_{z'z'}\text{.}\) For off-diagonal components, lets look at \(I_{x'y'}\text{.}\)

\begin{align*} I_{x'y'} \amp = - \sum m x'y' \\ \amp = - \sum m (x-a_x)(y-a_y) \\ \amp = - \sum m x y - \sum m a_xa_y + a_x\sum m y + a_y \sum m x \\ \amp = I_{xy} - \sum m a_xa_y + 0 + 0 = I_{xy} - \sum m a_xa_y \end{align*}

Similarly, for other off-diagonal components. Thus, although moment of inertia \({\bf I}\) was diagonal with origin of principal axes at CM, it is not diagonal if origin is not at CM.

Example 10.30. Radius of Gyration of a Sphere About an Axis Tangent to the Edge.

What is the radius of gyration of a solid sphere of mass \(M\) and radius \(R\) about an axis that is tangent to its surface? Assume the sphere to be of unform density.

Answer.

\(\sqrt{\frac{7}{5}}\, R\text{.}\)

Solution.

Recall the definition of radius of gyration. It’s the distance from the axis, usually denoted by \(R_G\text{,}\) such that moment of inertia about the axis is \(I = M R_G^2\text{.}\)

We will start with the previously known fact that moment of inertia of a sphere about an axis passing through the center is

\begin{equation*} I_0 = \frac{2}{5}MR^2. \end{equation*}

Now, we want moment of inertia about an axis \(A\) that is parallel to the axis through the CM but is at a distance \(R\) away. Hence, moment of inertia about \(A\) will be

\begin{equation*} I_A = I_0 + MR^2 = \frac{7}{5} MR^2. \end{equation*}

Now, to get radius of gyration, we equate this to \(MR_G^2\text{.}\) This gives us

\begin{equation*} R_G = \sqrt{\frac{7}{5}}\, R. \end{equation*}

Exercises 10.3.2 Exercises

1. Principal Moment of Inertia of Water Molecule.

Use symmetry arguments to guess principal axes and find moments of inertia about them for a water molecule with \(m_1=m_3=m\) and \(m_2=M\) and \(l\) being the bond length and \(\theta\) angle between the bonds. Use \(a=l\sin\theta/2\) and \(h=l\cos\theta/2\text{.}\)

Hint.

Use definition.

Answer.

\(I_{xx}\frac{2mM h^2}{M + 2m}\text{,}\) \(I_{yy}=2 m a^2\text{,}\) \(I_{zz} = I_{xx} + I_{yy}\text{.}\)

Solution.

In Figure 10.32 two principal axes are shown; \(z\)-axis is coming out of the page. I have used symmetry to place CM at the center of the horizontal divider. By placing \(2m\) at \(Q\) and \(M\) at \(P\text{,}\) we get

\begin{equation*} \bar{OP} = \frac{2m\,l\cos(\theta/2) }{M+2m} = \frac{2mh}{M+2m}. \end{equation*}

Distance \(OQ\) will be

\begin{equation*} \bar{OQ} = h - \bar{OP} = \frac{M\,h }{M+2m}. \end{equation*}

The horizontal distance of masses \(m\) are \(a = l\sin(\theta/2)\text{.}\) Now, we write Cartesian coordinates of the three masses, with \(m_1\) being the lower left corner.

\begin{align*} \amp x_1 = - a,\ \ y_1 = - \frac{M\,h }{M+2m},\ \ z_1 = 0.\\ \amp x_2 = 0,\ \ y_2 = \frac{2m\,h }{M+2m},\ \ z_2 = 0.\\ \amp x_3 = + a = -x_1,\ \ y_3 = - \frac{M\,h}{M+2m}=y_1,\ \ z_3 = 0. \end{align*}

The diagonal components of moment of inertia will be

\begin{align*} I_{xx} \amp = m_1 (y_1^2 + z_1^2) + m_2 (y_2^2 + z_2^2) + m_3 (y_3^2 + z_3^2) \\ \amp = 2m \left(\frac{M\,h }{M+2m}\right)^2 + M \left( \frac{2m\,h }{M+2m}\right)^2\\ \amp = \frac{2mM h^2}{M + 2m}. \end{align*}

\begin{align*} I_{yy} \amp = m_1 (x_1^2 + z_1^2) + m_2 (x_2^2 + z_2^2) + m_3 (x_3^2 + z_3^2) \\ \amp = 2m a^2 + M \times 0 = 2 m a^2. \end{align*}

Since this is a coplanar system, we must have

\begin{equation*} I_{zz} = I_{xx} + I _{yy} = 2m a^2 + \frac{2mM\,h^2 }{M+2m}. \end{equation*}

We can verify it by carrying out calculation explicitly.

\begin{align*} I_{zz} \amp = m_1 (x_1^2 + y_1^2) + m_2 (x_2^2 + y_2^2) + m_3 (x_3^2 + y_3^2) \\ \amp = 2m a^2 + 2m \left( \frac{M\,h }{M+2m} \right)^2 + M \left( \frac{2m\,h }{M+2m} \right)^2 \\ \amp = 2m a^2 + \frac{2mM\,h^2 }{M+2m}. \end{align*}

Let’s work out one of th eoff-diagonal components. Let’s say we want \(I_{xy}\text{.}\)

\begin{align*} I_{xy} \amp = - m_1 x_1 y_1 - m_2 x_2 y_2 - m_3 x_3 y_3 \\ \amp = - m x_1 y_1 - 0 - m (-x_1) (y_1) = 0. \end{align*}

Prev Top Next