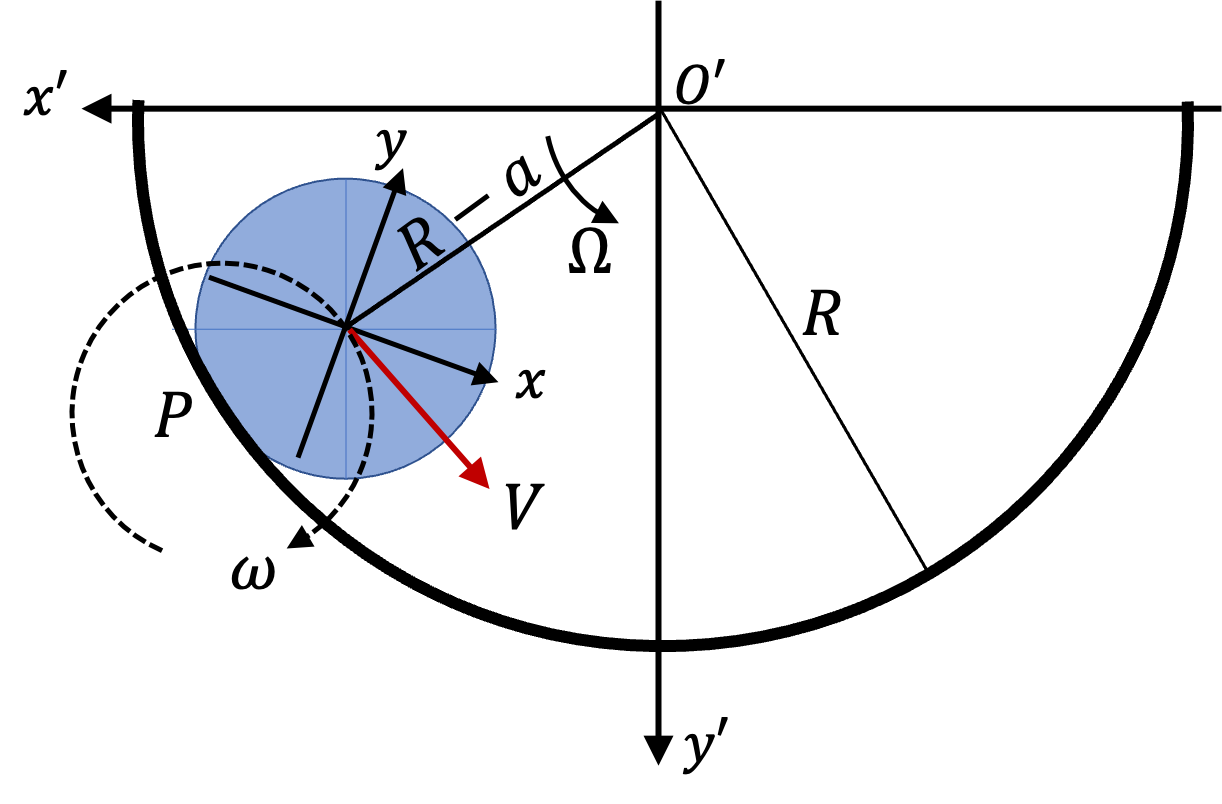
Example 10.5. Angular Velocity of a Rolling Wheel.
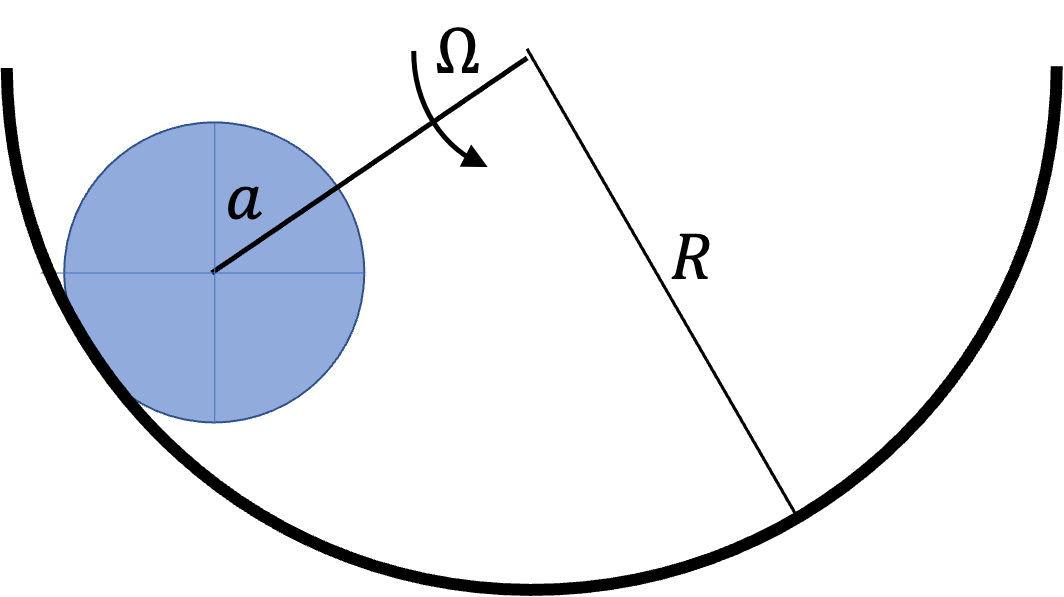
Figure 10.6 shows a wheel rolling on a flat plane without slipping. Suppose \(z\)-axis is coming out of the page. What will be the angular velocity vector?

Answer.
\(\vec \omega = - \frac{V}{R}\, \hat k\text{.}\)
Solution.
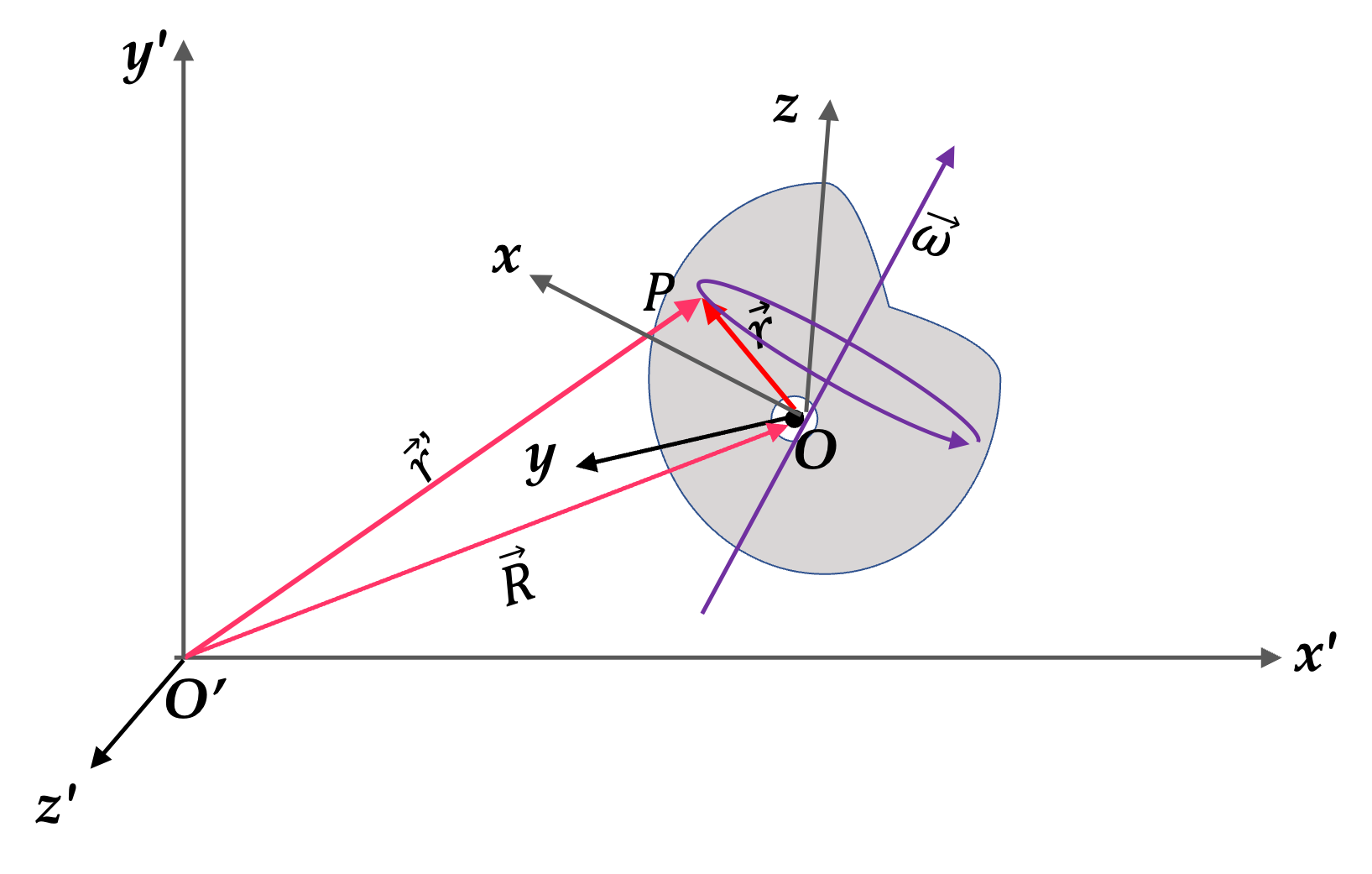
Figure 10.7 shows a fixed coordinate and a moving coordinate. The \(z\) and \(z'\) axes are coming out of page and not shown.
Point P that touches the surface is momentarily at rest. The CM will appear to move in a circle of radius \(R\) with speed \(V\text{.}\) Therefore, magnitude of angular velocity is
\begin{equation*}
\omega = \frac{V}{R}.
\end{equation*}
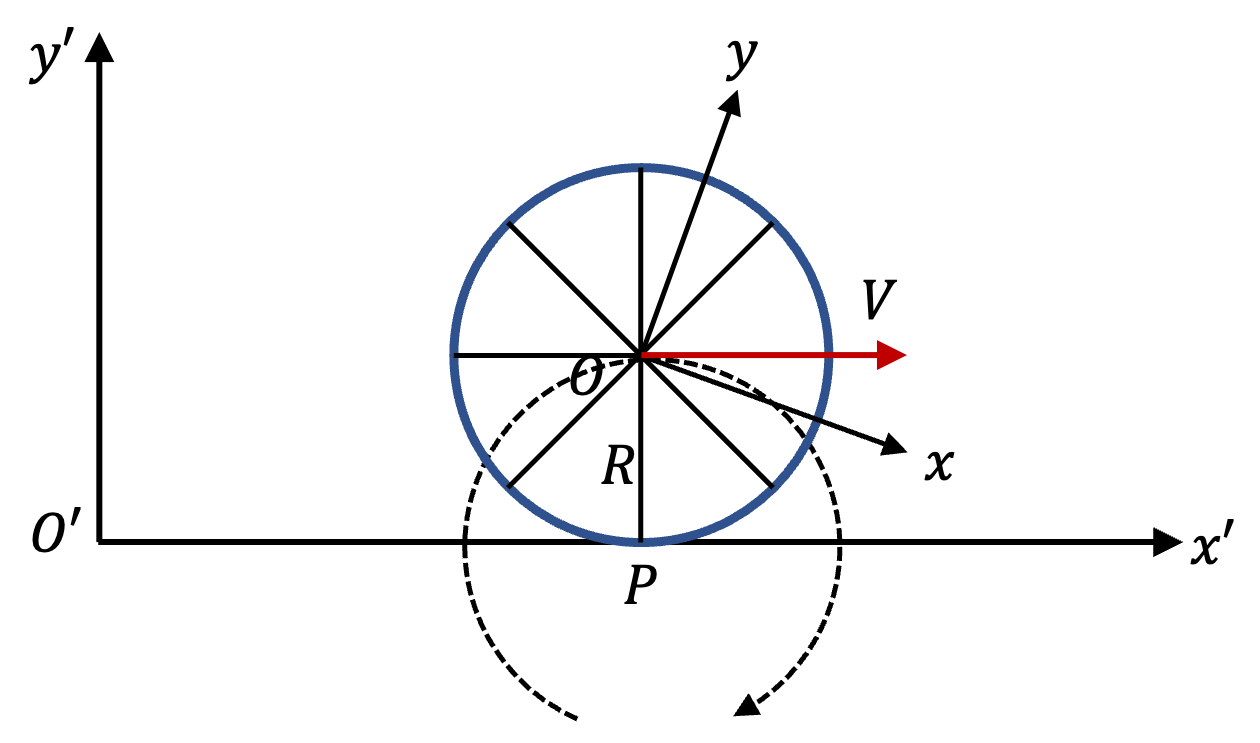
Axis of rotation is \(z\) axis and the sense of rotation is clockwise. That would make the orientation of axis in the negative \(z\)-axis direction. Therefore, angular velocity vector will be
\begin{equation*}
\vec \omega = - \frac{V}{R}\, \hat k.
\end{equation*}