Skip to main content
   
Logo image

Physics Bootcamp

Samuel J. Ling

Section 35.10 Magnetism Bootcamp

Exercises Exercises

Magnetic Force

1. Practicing Right-Hand Rule for Magnetic Force.
Follow the link: Example 35.18.
2. Magnetic Field from Motion of an Electron in a Magnetic Field.
Follow the link: Example 35.19.
3. Speed of a Proton Entering a Uniform Magnetic Field Region.
Follow the link: Exercise 35.4.3.1.

Magnetic Torque and Magnetic Potential Energy

4. Torque and Energy of an Electron in a MagneticField.
Follow the link: Example 35.21.
5. (Calculus) Force on a Magnet in an Inhomogeneous Magnetic Field.
Follow the link: Example 35.22.

Motion of Particles in Magnetic Field

6. Identifying Elementary Particles from Their Trajectories in Magnetic Field.
Follow the link: Example 35.26.
8. Cyclotron Frequency of an Electron in a Magnetic Field.
Follow the link: Example 35.28.
9. Bending of Trtajectory of an Alpha Particle in Magnetic Field.
Follow the link: Exercise 35.6.2.1.

Hall Effect

14. Using a Hall Probe to Measure Magnetic Field.
Follow the link: Example 35.34.
15. Determining the Sign of the Current Carrier in a Semiconductor.
Follow the link: Example 35.35.
16. Finding Hall Voltage from Given Geometry and Current Carrier Density.
Follow the link: Exercise 35.7.1.
17. Using Hall Effect to Determine Current Carrier Density in a Material.
Follow the link: Exercise 35.7.2.

Magnetic Force on Current-Carrying Wires

18. Force on a Current Carrying Wire by Two Magnets.
Follow the link: Example 35.39.
21. Force on a Square Current Loop Perpendicular to a Uniform Magnetic Field.
Follow the link: Exercise 35.8.5.3.
22. Force on a Square Current Loop with Normal at an Angle to a Uniform Magnetic Field.
Follow the link: Exercise 35.8.5.4.
23. (Calculus) Magnetic Force on a Current-Carrying Wire in an Inhomogeneous Magnetic Field.
Follow the link: Exercise 35.8.5.5.
24. (Calculus) Magnetic Force on a Current-Carrying Circular Arc in a Magnetic Field.
Follow the link: Exercise 35.8.5.6.
26. Magnetic Force in a Non-Uniform Magnetic Field 2.
Follow the link: Exercise 35.8.5.8.

Magnetic Torque on Current-Carrying Wires

27. Magnetic Dipole Moment of Current in a Triangular Loop.
Follow the link: Exercise 35.9.3.1.
29. Torques on Current Carrying Loop in Various Orientations.
Follow the link: Exercise 35.9.3.3.
31. Torque on a Loop Carrying Current Placed Between Poles of a Magnet.
Follow the link: Exercise 35.9.3.5.

Miscellaneous

32. Circular Motion by Both Electric and Magnetic Force on a Particle.
A particle of charge \(+q\) and mass m moves with velocity \(v_0\) pointed in the \(+y\)-direction as it crosses the \(x\)-axis at \(x=R\) at a particular time. There is a negative charge \(-Q\) fixed at the origin, and there exists a uniform magnetic field \(B_0\) pointed in the \(+z\)-direction. It is found that the particle describes a circle of radius \(R\) about \(-Q\text{.}\) Find \(B_0\) in terms of the given quantities.
Answer.
Check answer: If \(|Q|=4\pi\epsilon_0 R\text{,}\) and \(q/m = 2 v_02\text{,}\) then \(B_0 =1/(2v_0R)\text{.}\)
Solution.
The particle (mass \(m\text{,}\)charge \(+q\)) moves in a circle of radius \(R\) with the centripetal acceleration \(\dfrac{v_0^2}{R}\text{.}\) There are two radially-directed forces on the particle here: an electric force \(F_e\) from the charge \(-Q\) at the center of the circle, and a magnetic force \(F_m\) from the magnetic field which is pointed away from the center.
Figure 35.48.
Here \(F_e \gt F_m\) in order for the particle \(q\) to be moving in a circle about \(-Q\text{.}\) Therefore, we find the following equation of motion for \(q\text{.}\)
\begin{equation*} \left|\dfrac{1}{4\pi\epsilon_0}\: \dfrac{qQ}{R^2} \right| - \left| q v_0 B_0 \sin\:90^{\circ} \right| = m\:\dfrac{v_0^2}{R}. \end{equation*}
Solving for \(B_0\) we find
\begin{equation*} B_0 = \dfrac{1}{4\pi\epsilon_0}\: \dfrac{|Q|}{R^2v_0} - m\:\dfrac{v_0}{qR}. \end{equation*}
33. Trajectory of an Electron in a Magnetic Field.
Consider a region of space where magnetic field is uniform and is given to be \(B_x = 0\text{,}\) \(B_y = 0\) and \(B_z = 2\) mT. An electron which is first accelerated by a voltage difference of 500 V enters this region with its velocity pointed in the positive x-axis. (a) Find the acceleration of the electron. (b) Find an equation for the trajectory of the electron.
Answer.
(a) \(a = \frac{|e|B}{m}\,\sqrt{\frac{2|e|V}{m}}\text{,}\) (b) Circular trajectory of radius \(m v / e B\text{.}\)
Solution 1. a
To find the acceleration we will use \(a = F/m\) with \(F\) the magnetic force. Note that the speed of the electron which is accelerated by a voltage difference of \(V\) is obtained by energy conservation in this acceleration process.
\begin{equation*} \frac{1}{2}m v^2 = e V\ \ \longrightarrow\ \ v = \sqrt{\dfrac{2\:|e|\:V}{m}}. \end{equation*}
Using \(\vec F_m = Q\vec v \times \vec B\) we find the direction of the magnetic force is towards \(+y\)-axis and the magnitude is given by
\begin{align*} F_m \amp = |e|\: v\: B, \\ \amp = 1.6\times 10^{-19} v B, \end{align*}
Figure 35.49.
Now, using \(F_m\) as the net force in Newton’s second law of motion we obtain
\begin{equation*} a = \frac{|e|Bv}{m} = \frac{|e|B}{m}\,\sqrt{\frac{2|e|V}{m}}. \end{equation*}
in the positive \(y\)-direction.
Solution 2. b
Since \(vec B\) is pointed towards the \(z\)-axis and the electron enters the region with its velocity in the \(xy\)-plane, the trajectory will be a circle in the \(xy\)-plane. Let \(R\) be the radius of the circular trajectory, which is given by
\begin{equation*} R = \dfrac{mv}{|e|B}. \end{equation*}
Let \(x\)- and \(y\)-axes be chosen so that the particle enters the magnetic field region at \((x,y) = (0,-R)\) with the velocity pointed towards the positive \(x\)-axis. Then, the trajectory will be a circle with the center at the origin of the coordinate system. The equation of the circle will be
\begin{equation*} x^2 + y^2 = \left( \dfrac{mv}{|e|B} \right)^2. \end{equation*}
34. Helical Motion of a Proton in a Magnetic Field.
A proton of speed \(v_0= 6 \times 10^5\) m/s enters a region of uniform magnetic field of B =0.5 T at an angle \(\theta = 30^{\circ}\) to the magnetic field. In the region of magnetic field proton describes a helical path with radius \(R\) and pitch \(\lambda\) (distance between loops). Find \(R\) and \(\lambda\text{.}\)
Answer.
\(R = \dfrac{mv_0\sin\theta}{eB_0}\text{,}\) \(\lambda = (v_0\:\cos\theta)\: \ \dfrac{2\pi m}{e B_0} \text{.}\)
Solution.
Let the direction of the uniform magnetic field be towards the positive \(z\)-axis. The motion will then be a helical path with axis parallel to the \(z\)-axis. The projection of the motion in the \(xy\) plane will be a circular motion. Suppose the particle is crossing the \(xz\)-plane at \(t=0\) when it enters the magnetic field region.
Figure 35.50.
Since the velocity at this instant makes an angle \(\theta\) with respect to the direction of the magnetic field, the \(x\)-, \(y\)- and \(z\)-components of the velocity at this instant are given by
\begin{equation*} v_x = 0, \ \ v_y = v_0\:\sin\theta,\ \ v_z = v_0\:\cos\theta, \end{equation*}
where \(v_0 = 6\times 10^{5}\:\textrm{m/s}\) and \(\theta=30^{\circ}\text{.}\) The projection in the \(xy\)-plane describes a circular motion. By applying \(F = m a_c\) where \(F = F_m\text{,}\) the magnetic force and \(a_c\) the centripetal acceleration, we can show that the radius of the circle in the \(xy\)-plane will be
\begin{equation*} R = \dfrac{mv_0\sin\theta}{eB_0}. \end{equation*}
The pitch is the distance traveled parallel to the \(z\)-axis when the particle makes one complete circle in the projection in the \(xy\)-plane. The time \(T\) for one full circle is inverse of the cyclotron frequency,
\begin{equation*} T = \dfrac{2\pi}{\Omega} =2\pi \dfrac{m}{e B_0} . \end{equation*}
Therefore, the pitch \(\lambda\) of the helical path will be
\begin{equation*} \lambda = v_z\:T = (v_0\:\cos\theta)\: \ \dfrac{2\pi m}{e B_0}. \end{equation*}
35. Change in Speed of Electron in a Hydrogen Atom Under Applied Magnetic Field.
(a) Find the speed of the electron in a hydrogen atom if it moves in a circular orbit of radius \(0.0527\, \text{nm}\) about the proton. (b) If a uniform magnetic field of \(3\, \text{T}\) perpendicular to the circle of revolution is applied what will be the new speed and orbit size of the electron?
Answer.
(a) \(2.192 \times 10^6\, \text{m/s}\text{,}\) (b) \(R' = 53.5\ pm\text{,}\) \(v' = 2.175 \times 10^6\, \text{m/s}\text{.}\)
Solution 1. a
The central force for the uniform circular motion is provided by the electrostatic attraction from the proton. Therefore,
\begin{equation*} \dfrac{1}{4\pi\epsilon_0}\:\dfrac{e^2}{R^2} = m_e\:\dfrac{v^2}{R}, \end{equation*}
where \(v\) is the uniform speed of the electron and \(R\) the radius of the circular path. Solving for \(v\) we get
\begin{equation*} v = \sqrt{\dfrac{1}{4\pi\epsilon_0}\:\dfrac{e^2}{R m_e}} = 2.19\times 10^{6}\:\textrm{m/s}. \end{equation*}
Solution 2. b
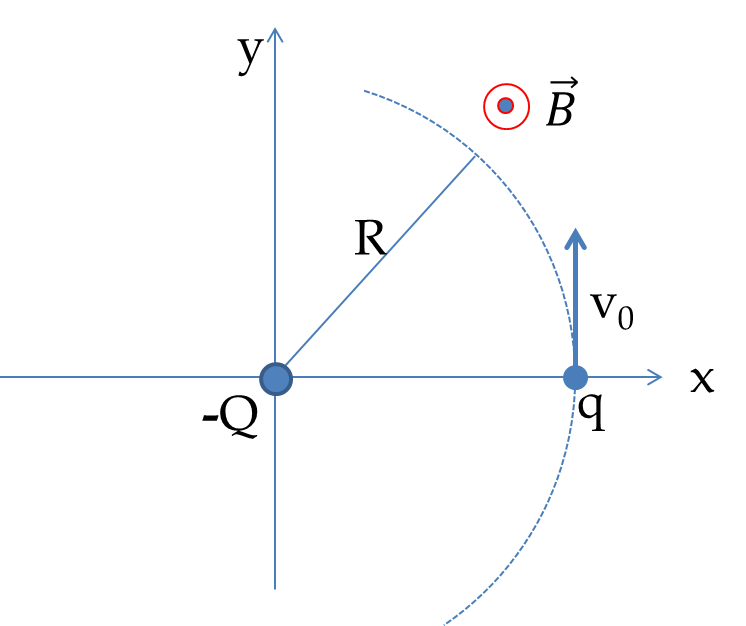
The new radius will depend upon the relative orientaiton of \(\vec v\) and \(\vec B\text{.}\) Let \(\vec B\) be oriented such that the magnetic force is pointed towards the nucleus. Denoting the new speed by \(v'\) and the new radius by \(R'\) we have
\begin{equation*} \dfrac{1}{4\pi\epsilon_0}\:\dfrac{e^2}{R'^2} + ev'B = m_e\:\dfrac{v'^2}{R'} \quad (1) \end{equation*}
Since the net force is radial, the angular momentum about an axis through the center will not change. Therefore,
\begin{equation*} m_e v R = m_e v' R'. \quad (2) \end{equation*}
Putting \(v'\) from (2) into (1) we get the following quadratic equation for the unknown \(R'\text{,}\)
\begin{align*} a\:R'^2 + \amp b\: R' + c = 0,\ \textrm{with} \\ \amp a = eRvB,\ \ b = \dfrac{e^2}{4\pi\epsilon_0},\ \ c = m_v^2 R^2. \end{align*}
Since \(R'>0\) we identify the following root for the solution.
\begin{equation*} R' = \dfrac{1}{2a}\:\left[ -b + \sqrt{b^2 -4 a c} \right] = 5.35\times 10^{-11}\:\textrm{m}. \end{equation*}
Now, using this value in (2) gives
\begin{equation*} v' = \left( \dfrac{R}{R'} \right)\: v = 2.18 \times 10^{6}\:\textrm{m/s}. \end{equation*}
36. Magnetic Force on a Hanging Rod with Current.
A copper rod of mass m and length \(L\) is hung from the ceiling using two springs of spring constant \(k\text{.}\) A uniform magnetic field of magnitude \(B_0\) pointing perpendicular to the rod and spring (coming out of the page in the figure) exists in a region of space covering a length \(w\) of the copper rod. The ends of the rod are then connected by flexible copper wire across the terminals of a battery of voltage \(V\text{.}\) Determine the change in the length of the springs when a current \(I\) runs through the copper rod in the direction shown in figure. (Ignore any force by the flexible wire.) Check answer: If \(IwB = 1\text{,}\) and \(mg = 2\text{,}\) then \(dy = 3/2k\text{.}\)
Figure 35.51.
Solution.
The forces on the rod are: (1) the magnetic force \(I\omega B_0\) pointed down, (2) the spring force \(2k\Delta y\) pointed up, and (3) weight \(mg\) pointed down. Since the rod does not have acceleration, the forces must be balanced giving
\begin{equation*} 2k\Delta y = I\omega B_0 + m g\ \ \Longrightarrow\ \ \Delta y = \dfrac{I\omega B_0 + m g}{2k}. \end{equation*}
37. Magnetic Force on an L-Shaped Conductor Carrying Current.
An \(L\)-shaped conductor sits on a table the ends of which are connected to the terminals of a DC power source resulting in a current \(I\) to flow in the conductor (see Figure). There is a uniform magnetic field \(B_0\) pointed perpendicular to the table. Find magnetic force on the \(L\)-shaped conductor.
Figure 35.52.
Answer.
Magnitude: \(IB\sqrt{a^2+b^2}\text{.}\)
Solution.
The magnetic forces on the two straight segments are easily obtained with magnitudes, \(F_1 = I a B\) pointed to the left on the vertical part, and \(F_2 = I b B\) pointed down on the horizontal part.
Therefore, the net force has the magnitude
\begin{equation*} F_{\textrm{net}} = I B \sqrt{a^2 + b^2}, \end{equation*}
and the direction given by the angle clockwise below the horizontal by \(\theta = \tan^{-1}(F_y/F_x) = \tan^{-1}(b/a)\text{.}\)
Figure 35.53.
PrevTopNext
Found typo?