Electric Field

Section 29.3 Electric Field

The Coulomb’s force law treats the interaction between charges as an action-at-a-distance. By action-at-a-distance we mean that a charge \(Q\) experiences force by another charge \(q\) which is not touching \(Q\text{.}\) One problem with the action-at-a-distance concept of a force is that, if you move \(q\text{,}\) the effect on \(Q\) is immediate regardless of their separation distance. This violates our notion of finite speed of travel of information.

The English physicist Michael Faraday (1791-1867) introduced the idea of electric field in 1830’s, which he called electric lines of force, in analogy with his earlier explanation of the arrangement of iron filings around a magnet, shown in Figure 29.24 in terms of the magnetic force lines. The iron filings respond to the magnetic force lines at their locations created by the magnet.

Credits for Figure 29.24 from Frank Eugene Austen (1916) Examples in Magnetism, 2nd Ed., Hanover, N.H., USA, p.31, plate 2 on Google Books, Public Domain, https://commons.wikimedia.org/w/index.php?curid=4632957.

Figure 29.24. Iron filings align with magentic field.

In analogy with the relation of magnetic field to magnetic force, Faraday believed that each charge created invisible electric lines of force, which would be electric field, and other charges responded to the electric field at their location. Imaginary lines of force emanating from every charge is a good way to visualize electrical effect a charge will have other charges. However, we do need a more quentiative way to study electric field.

Subsection 29.3.1 Definition of Electric Field

Following Faraday, we envision the entire space being permeated by invisible lines. At each point in space, they represent a vector, which we will call electric field vector. We will denote it by symbol \(\vec E\) or \(\vec E_P\text{,}\) where subscript \(P\) refers to the space point of interest. When we place a charge \(Q\) at point P, this charge will experience an electric force whose maganitude is

\begin{equation} F_e = Q\,E,\tag{29.13} \end{equation}

and the direction of the force is same as that of \(\vec E\) if \(Q\) is positive, and opposite to \(\vec E\) if \(Q\) is negative. The SI unit of electric field will be \(\text{N/C}\text{.}\) We can write force/electric field relation as a vector equation as

\begin{equation} \vec F = Q\, \vec E.\tag{29.14} \end{equation}

By measuring force on charge \(Q\text{,}\) we can deduce the electric field by dividing the measured force by charge.

\begin{equation} \vec E = \dfrac{\vec F}{Q}.\tag{29.15} \end{equation}

Note that charge \(Q\) is only “feeling” or “discovering” the electric field that already exists at its location due to other charges somewhere else. We call the \(feeler\) charge \(Q\) the test charge and the other charges whose electric field the test charge is responding to are called the source charge or just charges. The space point P, where we have placed charge \(Q\) is called the field point. It is important to note that:

Electric field at the field point exists regardless of whether or not we test its existence by placing the test charge at that point - it has been generated by other charges.

Example 29.25. Electric Force on a Proton Placed in an Electric Field.

A proton is placed at a point in space where electric field is \(300\text{ N/C}\text{.}\) Find the magnitude of acceleration of the proton.

Data: mass of proton = \(1.673\times 10^{-27}\text{ kg}\text{,}\) charge of proton = \(1.6\times 10^{-19}\text{ C}\text{.}\)

Answer.

\(2.87 \times 10^{10}\text{ m/s}^2\text{.}\)

Solution.

Acceleration can be obtained by applying Newton’s second law of motion with electric force on the electron.

\begin{align*} a \amp = \dfrac{F_e}{m} = \dfrac{qE}{m} \\ \amp = \dfrac{1.6\times 10^{-19}\text{ C} \times 300 \text{ N/C}}{ 1.673\times 10^{-27}\text{ kg}} \\ \amp = 2.87 \times 10^{10}\text{ m/s}^2. \end{align*}

Example 29.26. Suspending a Charged Droplet in Air.

An oil droplet of mass \(1.6\times 10^{-6}\text{ kg}\) is suspended in mid-air when an electric field of magnitude \(2.0\times 10^{4}\text{ N/C}\) and direction down is applied. (a) Find the amount of electic charge on the droplet. (b) How many excess electron or proton does the droplet have?

Data: \(e = 1.6\times 10^{-19}\text{ C}\text{.}\)

Answer.

(a) \(-7.85 \times 10^{-10}\text{ C}\text{,}\) (b) \(4.9\times 10^{9}\text{.}\)

Solution 1. (a)

There are two forces on the droplet, \(mg\) pointed down and \(qE\) pointed up. Since electric field is pointed down, but electric force is pointed up, the charge must be negative.

\begin{equation*} q = - \frac{mg}{E} = - \frac{ 1.6\times 10^{-6}\text{ kg} \times 9.81\text{ m/s}^2}{2.0\times 10^{4}\text{ N/C}} = -7.85 \times 10^{-10}\text{ C}. \end{equation*}

Solution 2. (b)

Dividing the charge by \(e\) will give us the excess electron on the droplet.

\begin{equation*} N_e = \frac{ 7.85 \times 10^{-10}\text{ C} } { 1.6\times 10^{-19}\text{ C} } = 4.9\times 10^{9}. \end{equation*}

Subsection 29.3.2 How Electric Field Solves the Action-at-a-Distance Problem?

With the viewpoint of electric force based on the electric field, there is no action-at-a distance. Instead, the electric force on the test charge \(Q\) is due to the local value of the electric field regardless of the source of electric field. When the source charge(s) of the electric field moves, it takes some time before the electric field at point P changes and the charge \(Q\) responds to the new electric field.

From the dynamic theory of electric fields one can show that the time taken to respond to a movement of the source charge will be equal to the time it would take light to travel from the source charge to the field point. The reason we see “instantaneous” response in the lab has to do with the fact that light travels at enormous speed of \(3\times 10^{8}\text{ m/s}\) and it takes only nano seconds in the lab setting, which is an imperceptible time.

Subsection 29.3.3 Electric Field of a Point Charge at Origin

Suppose a charge \(q\) is fixed to the origin of a Cartesian coordinate system. What is the electric field at point P a distant \(r\) from the charge? To find the electric field at P, let us place a positive “feeler” (test) charge \(Q\) at P, and deduce electric field by dividing the force on \(Q\) by the charge \(Q\text{.}\)

The magnitude of the force on \(Q\) is:

\begin{equation} \text{Magnitude:}\ \ \ F_{\text{on Q}} = \frac{1}{4\pi\epsilon_0}\frac{|Q|\ |q|}{r^2}\tag{29.16} \end{equation}

Now, we can factor the “feeler” charge \(Q\) and immediately obtain the magnitude of the electric field at P.

\begin{equation} \text{Magnitude:}\ \ \ E_P = \frac{1}{4\pi\epsilon_0}\frac{|q|}{r^2}.\tag{29.17} \end{equation}

The direction of the electric field is the direction of the force on a positively-charged test particle. Therefore, if the “source” charge \(q\) is positive, then the electric field at P would be pointed away from \(q\) and towards P, and when \(q\) is negative the electric field at P would have the direction from P towards \(q\text{.}\) See Figure 29.27.

Figure 29.27. The electric field of a positive charge is pointed away from the charge and that of a negative charge is pointed towards the charge. The electric field at a point, say P, is denoted by a vector \(\vec E_P\) at that point, which is shown by an arrow of length corresponding to the magnitude \(E_P\text{.}\)

Let me emphasize again that the electric field \(\vec E_P\) exists at every space point P whether or not the test charge is placed there. The test charge \(Q\) only “discovers” an electric field by experiencing a force when placed at that point.

Subsection 29.3.4 Electric Field Lines of a Single Charge

The vector arrows of electric field at various points produce a diagram of directed lines. These lines are called electric field lines. The electric field lines of a single positive charge are straight lines emanating from the charge in all directions as shown in Figure 29.27 and of a single negative charge are straight lines that terminate on the charge from all directions.

There is a notion of density of electric field lines that gives a quantitative sense in an electric field line diagram. The density of lines at a point is defined by “number of lines” that pass through a unit area pependicular to the lines at that point. You would draw more lines in the region where electric field is stronger and less in the areas with weaker field.

Figure to the right shows an electric field diagram of a single positive charge. At a distance \(r=1\text{ m}\text{,}\) the lines pass through an area of \(4\pi \text{ m}^2\text{,}\) the area of a spherical surface enclosing the charge. But same number of field lines pass through area \(4\pi \times 4\text{ m}^2\) at distance \(r = 2\text{ m}\text{.}\) Therefore, the electric field at at distance \(r = 2\text{ m}\) is \(\dfrac{1}{4} \) of that at at \(r = 1\text{ m}\text{.}\)

\begin{equation*} E_\text{at 2 m} = \dfrac{1}{4} E_\text{at 1 m}. \end{equation*}

Exercises 29.3.5 Exercises

1. Variation of Electric Field with Distance from a Charge.

You find that electric field from a point charge has a magnitude of \(300\text{ N/C}\) when you are \(20\text{ cm}\) from the charge. What will be the electric field from the same change when you look at a point that is \(40\text{ cm}\) from the charge?

Hint.

USe \(E\propto 1/r^2\text{.}\)

Answer.

\(75\text{ N/C}\text{.}\)

Solution.

Note that magnitude of electric field from a charge drops as square of the distance from the charge. Therefore, we will get

\begin{equation*} E_\text{at 40 cm} = \left( \frac{20\text{ cm} }{40\text{ cm}}\right)^2 \: E_\text{at 20 cm} = \frac{300\text{ N/C}}{4} = 75\text{ N/C}. \end{equation*}

2. Electric Field of a Point Charge at Origin.

A positive charge of magnitude \(2.0\text{ nC}\) is located at the origin. Find the magnitude and direction of the electric field at ten labeled points in the \(xy\)-plane shown in Figure 29.28.

Figure 29.28. Figure for Exercise 29.3.5.2.

Hint.

Use the definition.

Answer.

Magnitudes: \(E_1 = 18\text{ N}\text{,}\) \(E_2 = E_4 = E_5 = E_6 = 4.5\text{ N}\text{,}\) \(E_7 = E_8 = E_9 = E_{10} =1.38\text{ N}\text{.}\) Directions: From charge at origin to the points.

Solution.

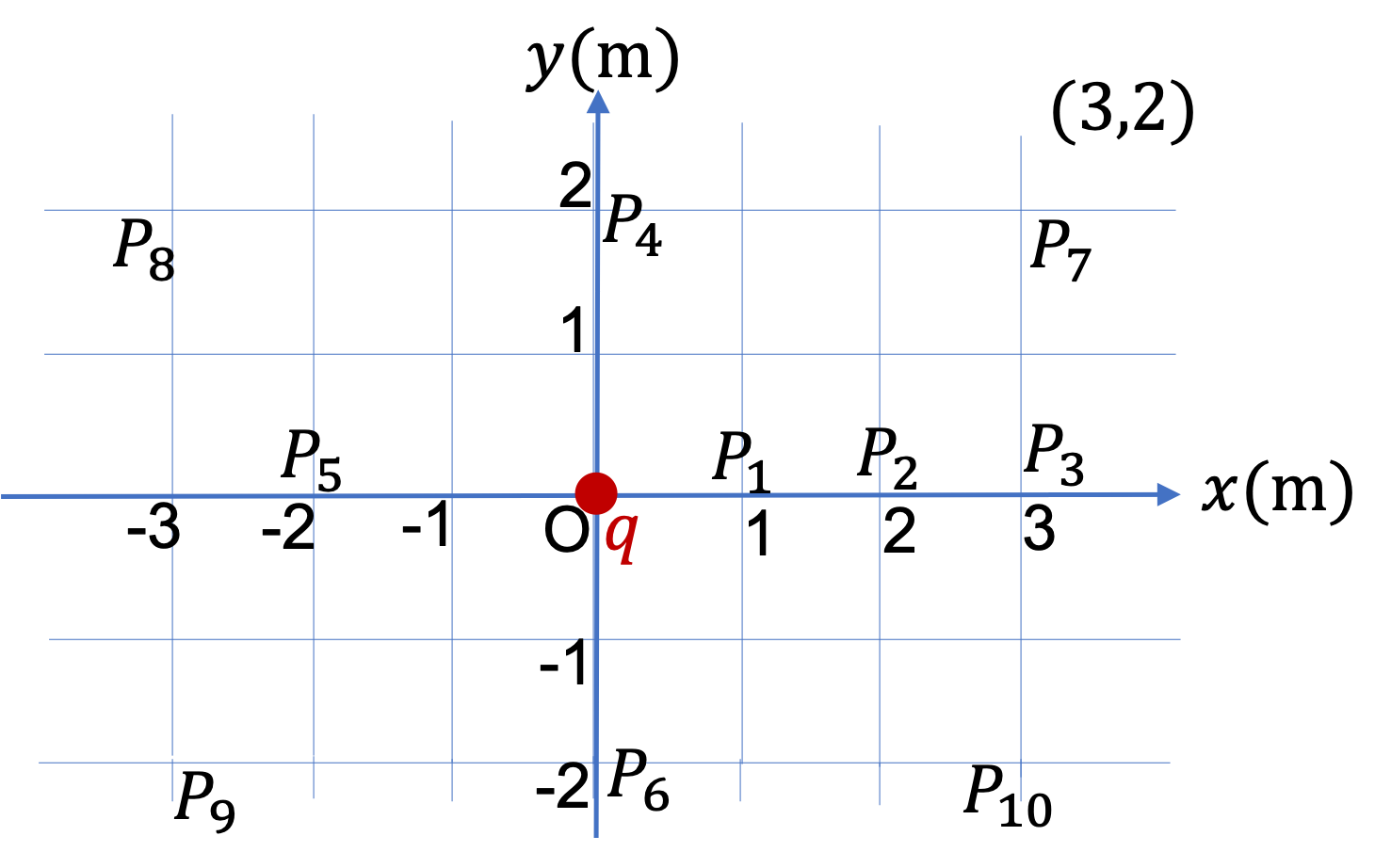
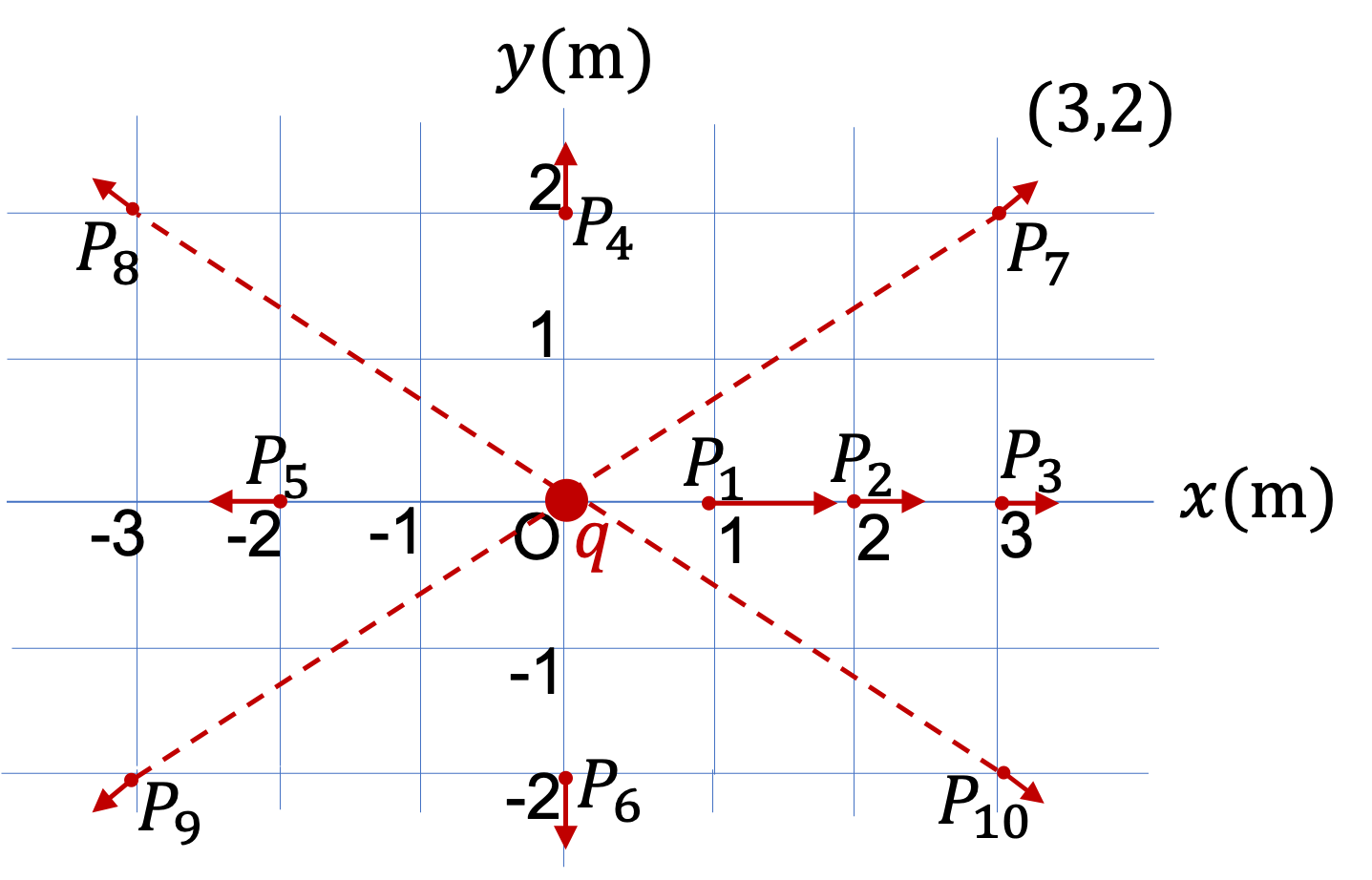
We will first work out the distances from the charge at the origin to the points in the question. We denote these distances by subscript, labeling the points.

\begin{align*} \amp r_1 = 1\text{ m},\ \ r_2 = 2\text{ m},\ \ r_3 = 3\text{ m},\\ \amp r_4 = 2\text{ m},\ \ r_5 = 2\text{ m},\ \ r_6 = 2\text{ m},\\ \amp r_7 = \sqrt{13}\text{ m},\ \ r_8 = \sqrt{13}\text{ m},\\ \amp r_9 = \sqrt{13}\text{ m},\ \ r_{10} = \sqrt{13}\text{ m}. \end{align*}

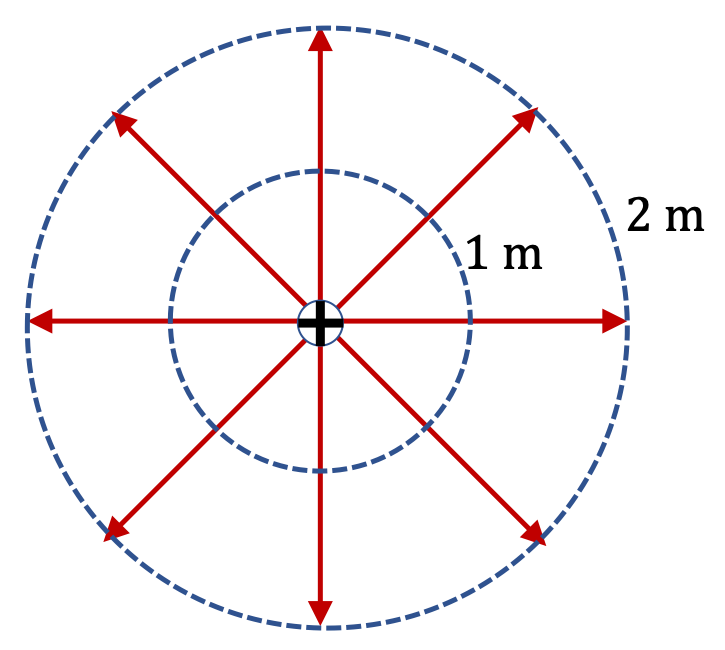
Same distance from the charge will have same magnitude of electric field. We have four different values of distance, so we need to wrok out four values. Actually, we need to work out only one value and use ratios of squares of distances to get the others.

\begin{align*} \amp E_1 = k\dfrac{q}{r_1^2} = 9\times 10^9 \times \dfrac{2\times 10^{-9}}{1^2} = 18\text{ N}. \\ \amp E_2 = E_4 = E_5 = E_6 = E_1\times\left( \dfrac{1\text{ m}}{2\text{ m}} \right)^2 = 4.5\text{ N}. \\ \amp E_7 = E_8 = E_9 = E_{10} = E_1\times\left( \dfrac{1\text{ m}}{\sqrt{13}\text{ m}} \right)^2 = 1.38\text{ N}. \end{align*}

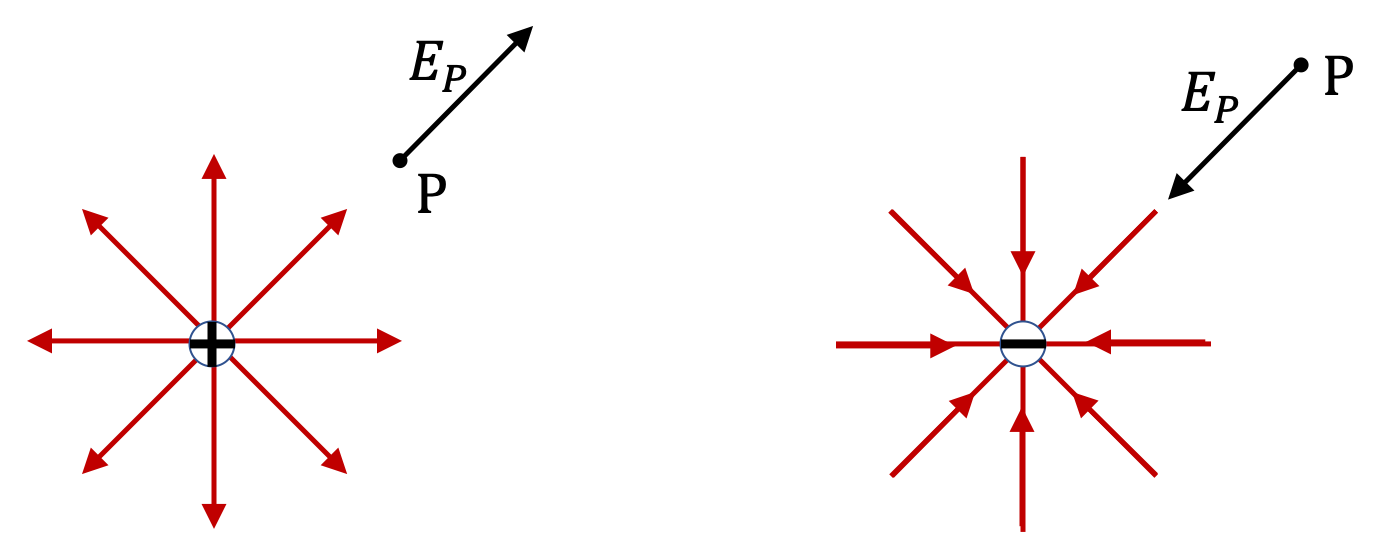
The directions of electric field at various points will be along the line from the charge to that point. Since charge is positive, the direction is directly away from the charge. Therefore, the directions are

\begin{gather*} \vec E_1:\text{ towards positive } x \text{ axis},\\ \vec E_2:\text{ towards positive } x \text{ axis},\\ \vec E_3:\text{ towards positive } x \text{ axis},\\ \vec E_4:\text{ towards positive } y \text{ axis},\\ \vec E_5:\text{ towards negative } x \text{ axis},\\ \vec E_6:\text{ towards negative } y \text{ axis}, \end{gather*}

For the direction of \(\vec E_7\) to \(\vec E_{10}\text{,}\) we will use angle in the \(xy\)-plane. For \(\vec E_7\text{,}\) we find that the direction from the charge to the point is in the direction that is at a counterclockwise angle \(\theta_7\) found by

\begin{equation*} \theta_7 = \tan^{-1}\left( \dfrac{2\text{ m}}{ 3\text{ m}} \right) = 33.7^\circ. \end{equation*}

Similar calculations for the three other points will show that \(\vec E_8\) is at a clockwise angle \(33.7^\circ\) from negative \(x\) axis, \(\vec E_9\) is at a counterclockwise angle \(33.7^\circ\) from negative \(x\) axis, and \(\vec E_{10}\) is at a clockwise angle \(33.7^\circ\) from positive \(x\) axis. Figure 29.29 summarizes the results.

Prev Top Next