Skip to main content
   
Logo image

Physics Bootcamp

Samuel J. Ling

Section 25.3 The Carnot Engine

In a Carnot engine a fixed amount of ideal gas is heated and cooled in a particular cyclic process called the Carnot cycle. The Carnot cycle consists of four steps shown in Figure 25.3.
  1. Isothermal expansion at high temperature \(T_H\text{.}\)
  2. Adiabatic expansion lowering temperature from \(T_H\) to \(T_C\text{.}\)
  3. Isothermal compression at lower temperature \(T_C\text{.}\)
  4. Adiabatic compression raising temperature from \(T_C\) to \(T_H\text{.}\)
The states A, B, C, and D are chosen so that at the end of these four steps, the system returns to state A.
Figure 25.3. The processes of the Carnot engine. Process AB is an isothermal expansion at temperature \(T_H\text{,}\) BC an adiabatic expansion, CD an isothermal compression at temperature \(T_C\text{,}\) and DC an adiabatic compression.
Since the system is an ideal gas and the processes are all quasi-static it is possible to work out heat and work in each step as we will show below. These calculations show that the ratio of \(Q_C \) to \(Q_H \) is equal to the ratio of the temperatures of the baths in absolute scale.
\begin{equation} \dfrac{Q_C}{Q_H} = \dfrac{T_C}{T_H}\ \ \text{(temperatures in kelvin scale)} \tag{25.4} \end{equation}
This relation can also used to define the absolute or kelvin scale of temperature from an operational viewpoint. Using this equaiton we can deduce the following for the efficiency of a Carnot engine.
\begin{equation} \eta_{\text{Carnot}}= 1-\dfrac{T_C}{T_H}\ \ \text{(temperatures in absolute/Kelvin scale)} \tag{25.5} \end{equation}
This formula for the efficiency of a Carnot engine says that a Carnot engine will be 100% efficient only if the temperature of the cold bath \(T_C \) were zero degree kelvin.
When this observation on the efficiency of the Carnot engine is combined with the Kelvin-Planck statement of the second law, we can conclude that a temperature of zero degree kelvin is not reachable since that would imply a possibility of constructing a thermal engine that has \(100\%\) efficiency. This gives another way to state the second law of thermodynamics.
Another Statement for the Second Law. It is impossible to reach a temperature of zero degree kelvin.

Subsection 25.3.1 Proof of \(Q_C/Q_H = T_C/T_H\) in Carnot Cycle

Since the internal energy of an ideal gas is proportional to temperature, the internal energy does not change in the processes AB and CD in Figure 25.3. Applying first law of thermodynamics to these steps and using the formula for work by a gas in an isothermal process, we conclude
\begin{align} \amp Q_H = W_{AB} = nRT_H \ln\left( \frac{V_B}{V_A} \right) \tag{25.6}\\ \amp Q_C = W_{CD} = nRT_H \ln\left( \frac{V_D}{V_C} \right) \tag{25.7} \end{align}
From the adiabatic processes BC and DA we have the following relations.
\begin{align*} \amp \textrm{BC process: } T_H V_B^{\gamma-1} = T_C V_C^{\gamma-1}\\ \amp \textrm{DA process: } T_H V_A^{\gamma-1} = T_C V_D^{\gamma-1} \end{align*}
Taking the ratio we find
\begin{equation} \frac{V_B}{V_A} = \frac{V_C}{V_D}. \tag{25.8} \end{equation}
Now, we take the ratio of Eq. (25.7) to Eq. (25.6) and use Eq. (25.8) to obtain the required result.
\begin{equation*} Q_C/Q_H = T_C/T_H. \end{equation*}

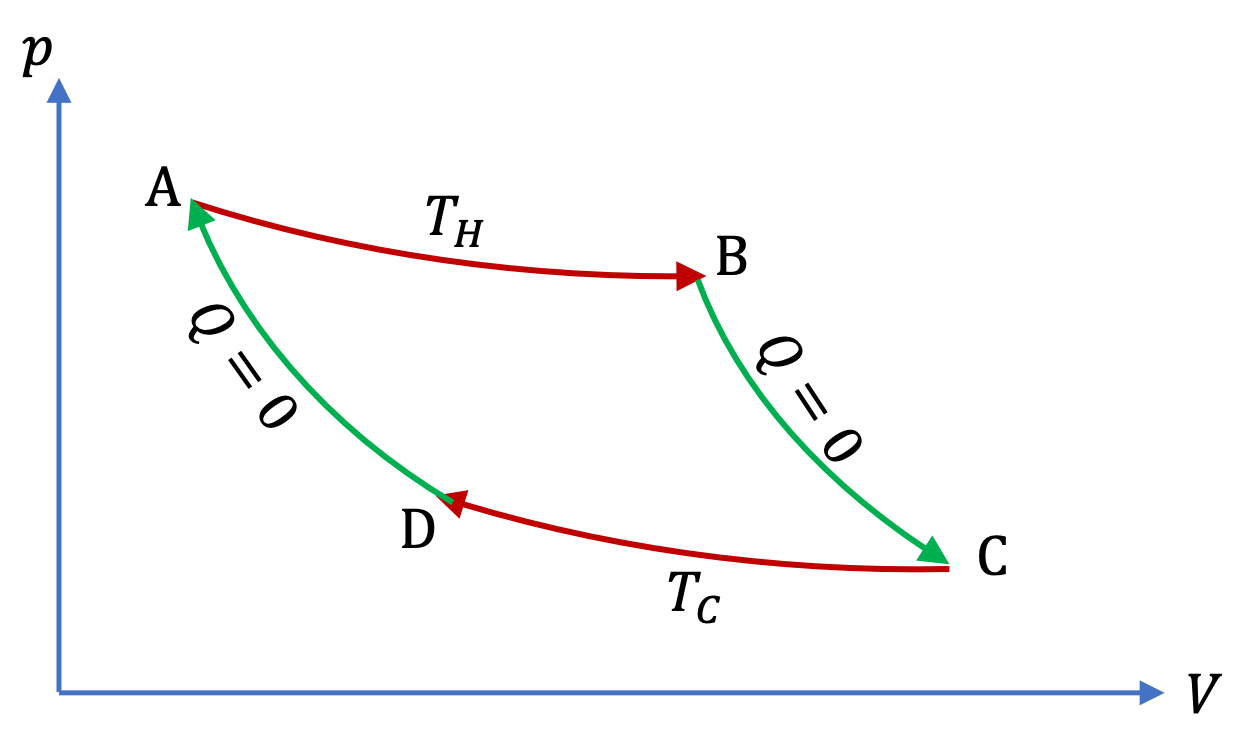
Example 25.4. The Efficiency of a Carnot Engine.

A Carnot engine operates between \(400^{\circ}\text{C}\) and \(27^{\circ}\text{C}\text{.}\)
(a) What is the efficiency of the Carnot engine?
(b) If the Carnot engine produces 5 kJ of work in each cycle, how much heat must it absorb from the \(400^{\circ}\text{C}\) bath in each cycle.
Answer.
(a) 55.4%, (b) \(9.03\ \text{kJ}\text{.}\)
Solution 1. (a)
(a) The efficiency of a Carnot engine can be written in terms of temperatures of the hot and cold baths. But, there is a catch. In order to make use of the formula for efficiency in terms of temperatures, we must express the temperatures in absolute scale.
\begin{align*} \amp T_H = 400 + 273.15 = 673.15\text{K} \\ \amp T_C = 27 + 273.15 = 300.15\text{K} \end{align*}
Therefore, the efficiency of the Carnot engine is
\begin{equation*} \eta = 1- \dfrac{T_C}{T_H} = 1 - \dfrac{300.15\text{K}}{673.15\text{K}} = 0.554. \end{equation*}
The efficiency in this formula is written as fraction. Normally, we write the number in percentage by multiplying this number by 100. This gives the efficiency of this engine to be 55.4%.
Solution 2. (b)
(b) We can use the efficiency found to figure out the heat in the engine.
\begin{equation*} \text{Since }\eta = \dfrac{W}{Q_H},\ \ Q_H = \dfrac{W}{\eta} = \dfrac{5\ \text{kJ}}{0.554} = 9.03\ \text{kJ}. \end{equation*}

Example 25.5. Heat Flow in a Carnot Engine.

A Carnot engine operating in a Carnot cycle between \(400^{\circ}\text{C}\) and an unknown lower temperature has an efficiency of \(0.3\text{.}\) How much heat must be rejected to the cold bath for every kJ of heat absorbed from the hot bath.
Answer.
\(0.7\,\text{kJ}\text{.}\)
Solution.
The efficiency of the Carnot engine can be expressed in terms of \(Q_C\) and \(Q_H\) alone.
\begin{equation*} \eta_C = \frac{Q_H-Q_C}{Q_H}\ \ \Longrightarrow\ \ Q_C = (1-\eta_C) Q_H. \end{equation*}
Therefore, if \(Q_H = 1\text{ kJ}\text{,}\) then
\begin{equation*} Q_C = (1-0.3) \times 1\ \text{kJ} = 0.7\ \text{kJ}. \end{equation*}

Exercises 25.3.2 Exercises

1. Efficiency of a Carnot Engine from Temeperatures of Baths Given in Celsius.

A Carnot engine operates in a Carnot cycle between a heat source at \(550^{\circ}\)C and a heat sink at \(20^{\circ}\)C. Find the efficiency of the Carnot engine.
Answer.
\(64.4\%\text{.}\)
Solution.
Recall that the temperatures in the Carnot efficiency formula are in the Absolute or Kelvin scale. Since the difference in temperature is same in Celsius and Kelvin scales, we only need to change the quantity that stands alone and not in the difference.
\begin{equation*} \eta_{\textrm{Carnot}} = \frac{T_H-T_C}{T_H} = \frac{550-20}{550+273.15} = \frac{530}{823.15} = 0.644\ \ \textrm{or}\ \ 64.4\%. \end{equation*}

2. Power of a Carnot Engine.

A Carnot engine working between two heat baths of temperatures \(600\text{K}\) and \(273\text{K}\) completes each cycle in \(5\text{ sec}\text{.}\) In each cycle, the engine absorbs \(10\text{ kJ}\) of heat. Find the power of the engine.
Hint.
Find \(\eta\) from temperatures and then use it to get \(W\) and \(P=W/\Delta t\text{.}\)
Answer.
\(2,400\text{ W}\text{.}\)
Solution.
The power \(P\) of the engine will be work \(W\) divided by time \(\Delta t\text{.}\)
\begin{equation*} P = \frac{W}{\Delta t}. \end{equation*}
From the definition of efficiency we can obtain \(W\) from the heat rejected to the lower temperature bath and the efficiency as follows.
\begin{equation*} \eta = \frac{W}{Q_H} = \frac{W}{W-Q_C}\ \ \Longrightarrow\ \ W = \left( \frac{\eta}{1-\eta}\right)\ Q_C. \end{equation*}
The efficiency here is equal to the efficiency of the Carnot cycle.
\begin{equation*} \eta = 1- \frac{T_C}{T_H}\ \ \Longrightarrow\ \ \frac{\eta}{1-\eta} = \frac{T_H-T_C}{T_C}. \end{equation*}
Putting in the values here
\begin{equation*} \frac{\eta}{1-\eta} = \frac{600-273}{273} = 1.2. \end{equation*}
Therefore,
\begin{equation*} W = 1.2\times\ Q_C = 1.2\times 10\ \text{kJ} = 12\ \text{kJ}. \end{equation*}
This work is done in 5 sec. Therefore, the power is
\begin{equation*} P = \frac{W}{\Delta t} = \frac{12\ \text{kJ}}{5\ s} = 2400\ \text{W}. \end{equation*}

3. Heat Required by a Carnot Engine to Power a Motor.

An engine working in a Carnot cycle between two heat baths of temperatures \(600\)K and \(273\)K runs an electric motor rated at \(60\) W of power (assume running the motor costs \(60\) W). If each cycle is completed in \(10\) seconds, how much heat does the engine absorb from the higher-temperature bath in each cycle?
Answer.
\(1101\ \textrm{J}\text{.}\)
Solution.
The efficiency
\begin{equation*} \eta = \frac{T_H - T_C}{T_H} = \frac{327}{600} = 0.545. \end{equation*}
The work output in each cycle is
\begin{equation*} W = P\Delta t = 60\ \textrm{W}\times 10\ \textrm{s} = 600\ \textrm{J}. \end{equation*}
Therefore
\begin{equation*} Q_{in} = \frac{W}{\eta} = \frac{600\ \textrm{J}}{0.545} = 1101\ \textrm{J}. \end{equation*}

4. Carnot Cycle with Monatomic Ideal Gas.

Two moles of a monatomic ideal gas performs a Carnot cycle between \(300\text{ K}\) and \(500\text{ K}\text{.}\) The starting volume of the gas before isothermal expansion was \(3\times 10^{-3}\text{ m}^3\text{,}\) and it expands to double the volume in the isothermal step. Find the total amount of work done and heat absorbed from the high temperature reservoir in each cycle.
Hint.
At any point of the cycle, use ideal gas law. For work for processes use \(-pdV\text{.}\) For internal energy use \((f/2)nRT\text{,}\) with \(f=3\) for monatomic gas.
Answer.
\(W = 774\text{ J}\text{,}\) \(Q_{H} = 1935 \text{ J}\text{.}\)
Solution.
First we find the \((p,V)\) at the vertices of the cycle.
\begin{align*} A:\ \ \amp \\ \amp T_A = 500\ \text{K}\\ \amp V_A = 3\times 10^{-3}\ \text{m}^3\\ \amp p_A = 2\times \frac{8.31\times 500}{3\times 10^{-3}} = 2.77\ \text{MPa} \end{align*}
B:
\begin{align*} \amp T_B = 500\ \text{K}\\ \amp V_B = 2\times 3\times 10^{-3}\ \text{m}^3 = 6\times 10^{-3}\ \text{m}^3\\ \amp p_B = \frac{2.77}{2}\ \text{MPa} =1.39 \ \text{MPa} \end{align*}
C:
\begin{align*} \amp T_C = 300\ \text{K}\\ \amp V_C^{\gamma-1} =\frac{T_B}{T_C} V_B^{\gamma-1} \ \ \Longrightarrow\ \ V_C = 12.9\times 10^{-3}\ \text{m}^3\\ \amp p_C = \frac{2 \times 8.31\times 300}{12.9\times 10^{-3}} = 0.386\ \text{MPa} \end{align*}
D:
\begin{align*} \amp T_D = 300\ \text{K}\\ \amp V_D^{\gamma-1} =\frac{T_A}{T_D} V_A^{\gamma-1} \ \ \Longrightarrow\ \ V_D = 6.45\times 10^{-3}\ \text{m}^3\\ \amp p_D V_D = p_C V_C \ \ \Longrightarrow\ \ p_D = 0.773\ \text{MPa} \end{align*}
The calculations for the work by the gas give.
\begin{align*} \amp W_{AB} = n R T_A \ln \frac{V_B}{V_A} = 5760\ \text{J}\\ \amp W_{BC} =\frac{3 n}{2} R (T_B -T_C) = 4986\ \text{J}\\ \amp W_{CD} = n R T_C \ln \frac{V_D}{V_C} = - 3456\ \text{J}\\ \amp W_{DA} =\frac{3 n}{2} R (T_D -T_A) = -4986\ \text{J} \end{align*}
The net work for the entire cycle is obtained by adding the work in each step.
\begin{equation*} W = 2304\ \text{J}. \end{equation*}
The Carnot efficiency of the cycle is given by
\begin{equation*} \eta = 1-\frac{300\ \text{K}}{500\ \text{K}} = 0.4. \end{equation*}
Therefore the cycle abosrbs the following energy from the higher-temperature source.
\begin{equation*} Q_{in} = \frac{W}{\eta} = \frac{2304\ \text{J}}{0.4} = 5760\ \text{J}. \end{equation*}
This is same as the work done in the AB part of the cycle since the change in the internal energy for a constant temperature process of an ideal gas is zero.

5. Numerical Study of Carnot Cycle.

A Carnot engine employs \(1.5\) moles of the Nitrogen gas as the working substance, which will be considered as a diatomic ideal gas with \(\gamma = 7/5\) at the working temperatures of the engine. The Carnot cycle goes in the cycle A-B-C-D-A with A-B being the isothermal expansion. The volume at points A and C of the cycle are \(5 \text{ L}\) and \(150 \text{ L}\) respectively. The engine operates between two thermal baths of temperature \(500\text{K}\) and \(300\text{K}\text{.}\)
  1. Find the values of the volume at B and D.
  2. How much heat is absorbed by the gas in the AB-isothermal expansion?
  3. How much work is done by the gas in the AB-isothermal expansion?
  4. How much heat is given up by the gas in the CD-isothermal compression?
  5. How much work is done by the gas in the CD-isothermal compression?
  6. How much work is done by the gas in the BC-adiabatic expansion?
  7. How much work is done by the gas in the DA-adiabatic compression?
  8. Find the value of the efficiency of the engine based on the net work and heat input. Compare this value of the efficiency to the value of the efficiency of the Carnot engine based on the temperatures of the two baths.
Hint.
At any point of the cycle, use ideal gas law. For work for processes use \(-pdV\text{.}\) For internal energy use \((f/2)nRT\text{,}\) with \(f=5\) for diatomic gas.
Answer.
\(V_B = 41.8 \text{ L}\text{,}\) \(Q_{AB} = 13,200\text{ J}\text{,}\) \(W_{AB} = Q_{AB} = 13,200 \text{ J}\text{,}\) \(Q_{CD}=-8,000\text{ J}\text{,}\) \(W_{CD}=-8,000\text{ J}\text{,}\) \(W_{BC} = 6,200\ \text{J}\text{,}\) \(W_{DA} = -6,200\ \text{J}\text{,}\) \(\eta = 0.394\text{.}\)
Solution.
We have the following known quantities in the Carnot cycle.
\begin{align*} \amp V_A = 5\ \text{L};\ \ V_C = 150\ \text{L}\\ \amp T_A = T_B = 500\text{K};\ \ T_C= T_D = 300\text{K} \end{align*}
The other parameters we have are
\begin{equation*} n = 1.5\ \text{mol};\ \ \gamma = \frac{7}{5} \end{equation*}
  1. Find the values of the volume at B and D. The process DA is adiabatic process. Therefore,
    \begin{equation*} T_A V_A^{\gamma-1} = T_D V_D^{\gamma-1}. \end{equation*}
    This gives
    \begin{equation*} V_D = \left(T_A/ T_D\right)^{1/(\gamma-1)}\ V_A = \left(\frac{500}{300}\right)^{5/2}\times 5\ \text{L} = 17.9\ \text{L}. \end{equation*}
    From the adiabatic process BC we get
    \begin{equation*} V_B = 41.8 \text{ L}. \end{equation*}
  2. How much heat is absorbed by the gas in the AB-isothermal expansion?
    \begin{align*} Q_{AB} \amp = n RT_A \ln\left( \frac{V_B}{V_A}\right)\\ \amp = 1.5\times8.31\times 500\times \ln\left( \frac{41.8}{5}\right) = 13,200\ \text{J} \equiv Q_H. \end{align*}
  3. How much work is done by the gas in the AB-isothermal expansion? Since the temperature is constant, and for an ideal gas, the internal energy does not change in a constant-temperature process.
    \begin{equation*} W_{AB} = Q_{AB} = 13,200\ \text{J}. \end{equation*}
  4. How much heat is given up by the gas in the CD-isothermal compression?
    \begin{align*} Q_{CD} \amp = n RT_A \ln\left( \frac{V_D}{V_C}\right)\\ \amp = 1.5\times8.31\times 300\times \ln\left( \frac{17.9}{150}\right) = -8,000\ \text{J} \equiv -Q_C. \end{align*}
  5. How much work is done by the gas in the CD-isothermal compression?
    \begin{equation*} W_{CD} = Q_{CD} = -8,000\ \text{J}. \end{equation*}
  6. How much work is done by the gas in the BC-adiabatic expansion? The adiabaticity of process gives the following for the work by the gas.
    \begin{equation*} W_{BC} = -\Delta U = -\frac{5}{2} n R(T_C - T_B) = 6,200\ \text{J}. \end{equation*}
  7. How much work is done by the gas in the DA-adiabatic compression? The adiabaticity of process gives the following for the work by the gas.
    \begin{equation*} W_{DA} = -\Delta U = -\frac{5}{2} n R(T_A - T_D) = -6,200\ \text{J}. \end{equation*}
  8. Find the value of the efficiency of the engine based on the net work and heat input. Compare this value of the efficiency to the value of the efficiency of the Carnot engine based on the temperatures of the two baths. The net work:
    \begin{align*} W \amp = W_{AB} + W_{BC} + W_{CD} + W_{DA} \\ \amp = 13,200\ \text{J} + 6,200\ \text{J} -8,000\ \text{J} -6,200\ \text{J} = 5,200 \ \text{J}. \end{align*}
    The heat input in the AB-process is
    \begin{equation*} Q_H = 13,200\ \text{J}. \end{equation*}
    Therefore, the efficiency of the cycle is
    \begin{equation*} \eta =\frac{5,200 \ \text{J}}{13,200\ \text{J}} = 0.394\ \ \text{or}\ \ 39.4\%. \end{equation*}
PrevTopNext
Found typo?