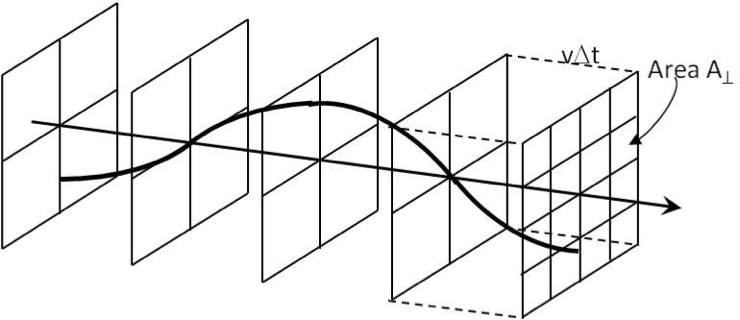
All waves
transport energy without an actual transport of material. For concreteness, as shown in
Figure 14.24 consider a wave of frequency
\(f\text{,}\) wavelength
\(\lambda\text{,}\) and amplitude
\(D\) on a taut string with tension
\(T\) and mass per unit length
\(\mu\text{.}\) We denote the amplitude of the displacement of string particles by letter
\(D\) rather than letter
\(A\) since the later will be used for area below. Supposing the wave is moving in the positive
\(x\) axis direction wave will have the following expression.
\begin{equation*}
\psi = D \cos\left( \frac{2\pi}{\lambda} x - 2\pi f t\right).
\end{equation*}
In
Figure 14.24, the energy of the wave will be contained in the motion (kinetic energy) and the deformation (potential energy). Let us figure out the energy contained within a distance
\(v\Delta t\) of the plane labeled
\(A_\perp\) in the figure. Since each part of the string executes simple harmonic motion at frequency
\(f\) of the wave, we can use formulas for energy derived in the simple harmonic motion to get some ideas about energy involved here. Let
\(K\) stand for effective spring constant (we use capital
\(K\) to distinguish it from wavenumber
\(k\)) and
\(M\) the mass of string in length
\(v\Delta t\text{,}\) where
\(v\) is the wave speed. Let
\(V\) denote maximum speed of motion of particles of string. Thus, average energy within a length
\(v\Delta t\) of the string can be estimated to be
\begin{equation}
E_\text{av} = \frac{1}{2} K D^2 = \frac{1}{2} M V^2\tag{14.54}
\end{equation}
Additionally, by analogy with simple harmonic oscillator, we can replace \(V\) by
\begin{equation}
V = \omega D= 2\pi f D.\tag{14.55}
\end{equation}
Using this we find
\begin{equation}
K = M \omega^2 = 4\pi^2 M f^2.\tag{14.56}
\end{equation}
Therefore,
\begin{equation}
E_\text{av} = \frac{1}{2} K D^2 = 2 \pi^2 M f^2 D^2.\tag{14.57}
\end{equation}
This energy will pass any point of string in time \(\Delta t\text{.}\) Therefore, the average rate of flow of energy, i.e., average power \(P\text{,}\) in the string will be
\begin{align}
P_\text{av} \amp = \frac{E_\text{av}}{\Delta t} = \frac{2 \pi^2 M f^2 D^2}{\Delta t}, \notag\\
\amp = \frac{2 \pi^2 M v f^2 D^2}{v\Delta t} = 2 \pi^2 \mu v f^2D^2, \notag\\
\amp = 2 \pi^2 \mu \lambda f^3 D^2, \tag{14.58}
\end{align}
This says that the rate at which energy is transported by a wave is proportional to the square of the amplitude of the wave.
\begin{equation}
P_\text{av} \propto D^2.\tag{14.59}
\end{equation}
It is of interest to know how “concentrated” the power is in any region. Therefore, we define a property called intensity of the wave by dividing power by the area of the surface the wave is flowing through, here it will be \(A_\perp\text{.}\)
\begin{equation}
I = \frac{P_\text{av}}{A_\perp} = \frac{2 \pi^2 \mu \lambda f^3 D^2}{A_\perp}.\tag{14.60}
\end{equation}
Imporant observation here again is that intensity of a wave is proportional to the square of the amplitude.
\begin{equation}
I \propto D^2.\tag{14.61}
\end{equation}
For a plane wave intensity does not change from one location to another or with time. This is not the case for spherical wave as we will see below.
Note that
\(D\) in Eq.
(14.60) has the units of length since it corresponds to displacement in its derivation. The unit of intensssity will be
\begin{equation*}
\text{unit of } I = \frac{\text{kg}}{\text{m}} \times \frac{1}{\text{s}^3} \frac{\text{m}^2}{\text{m}^2} = \frac{\text{W}}{\text{m}^2},
\end{equation*}
where \(\text{W}\) is Watts or \(\text{J/s}\text{.}\)