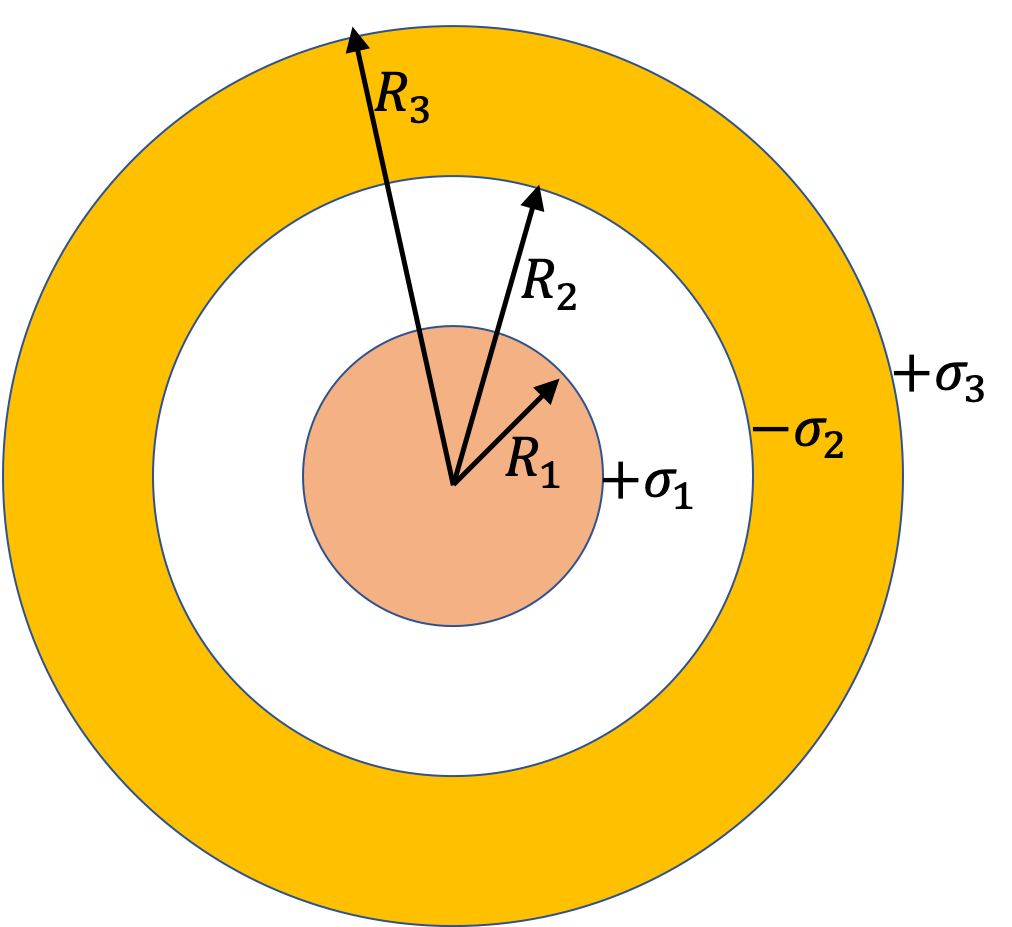
Example 30.17. Electric Field of Charged Thick Concentric Spherical Shells.
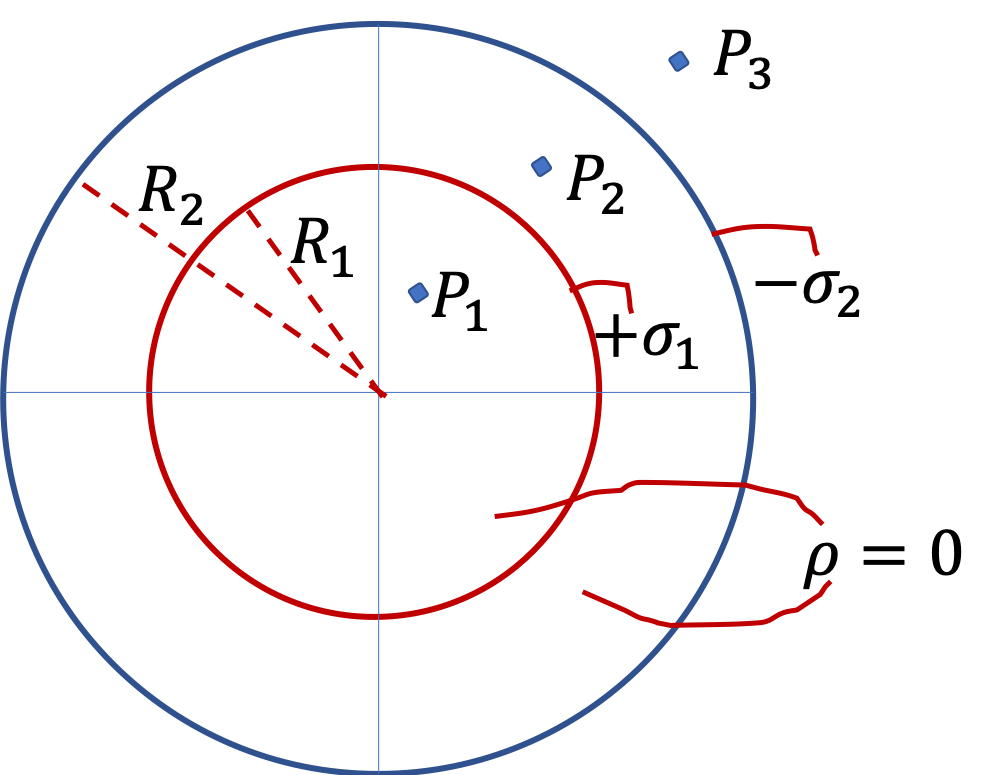
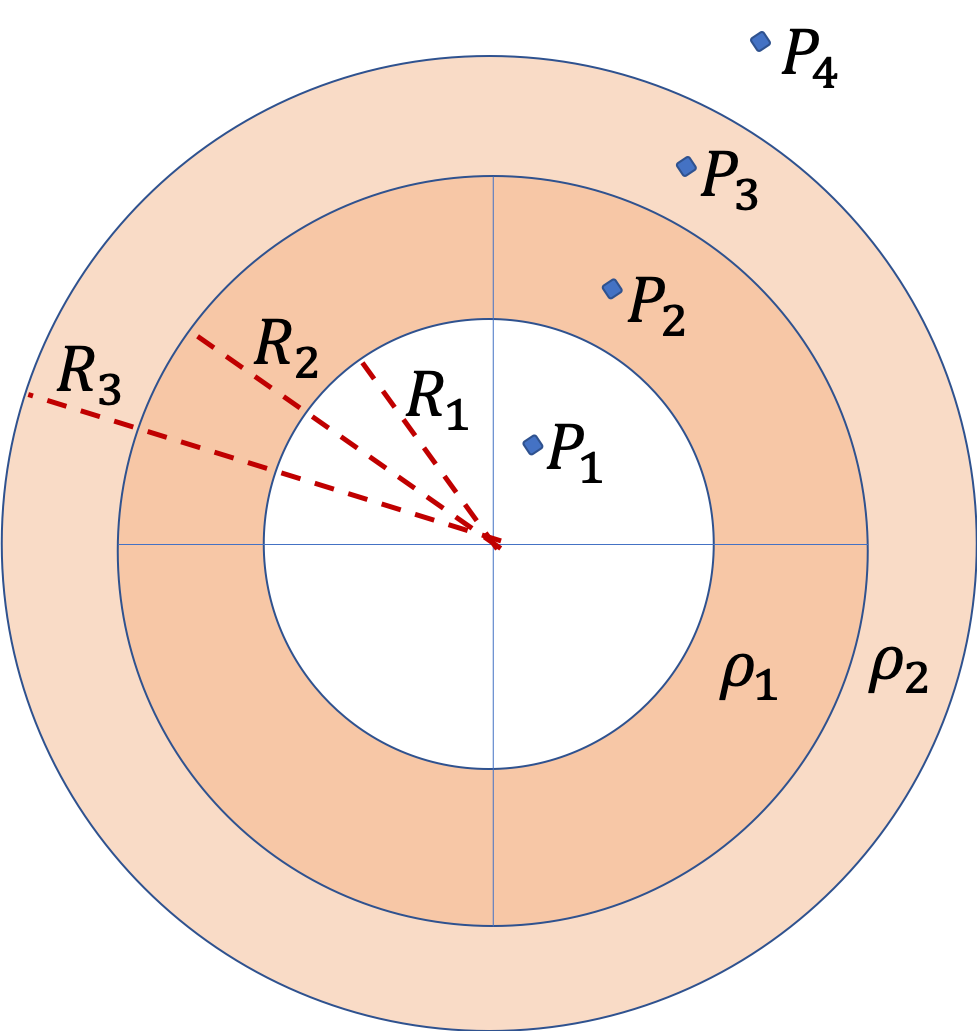
Figure shows two charged concentric spherical shells. There are no charges in the space at the core, i.e., charge density, \(\rho = 0,\ r\lt R_1\text{.}\) There are four distinct field points, labeled, \(P_1\text{,}\) \(P_2\text{,}\) \(P_3\text{,}\) and \(P_4\text{.}\) Find electric fields at these points.
Answer.
See solution.
Solution.
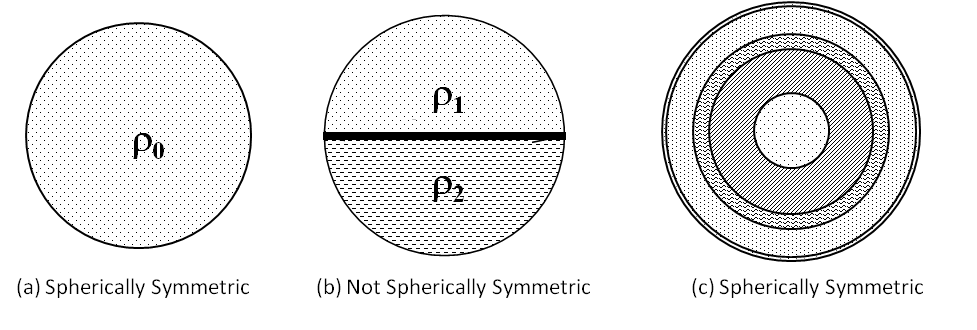
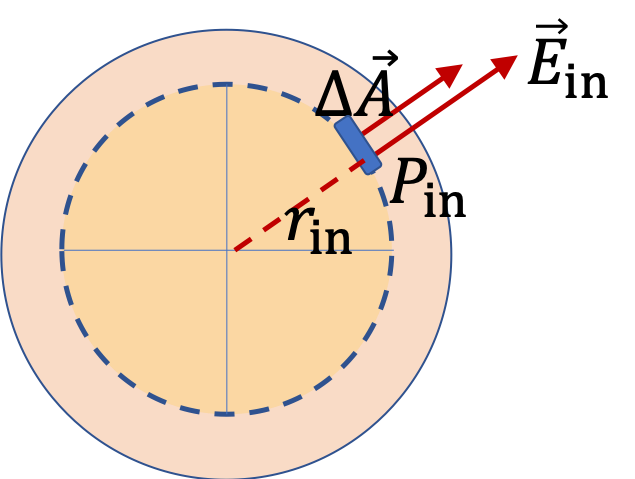
We first note that the charge distribution has a spherical symmetry since charge density is a function only of \(r\text{,}\) the distance from the common center, and not on the direction. That means, we can use Gauss’s law to find electric field rather easily.
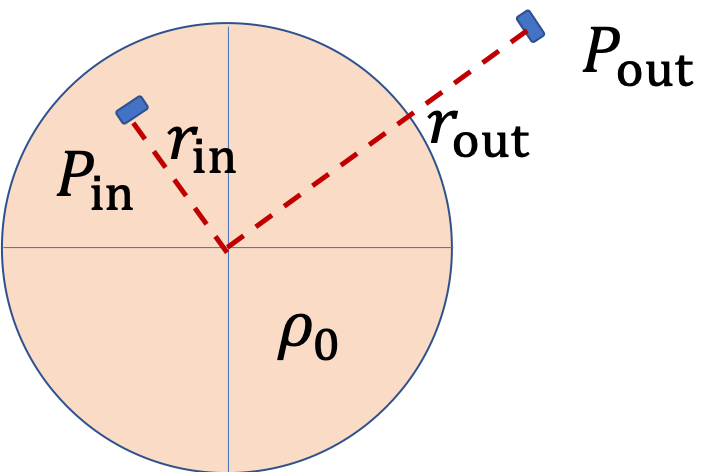
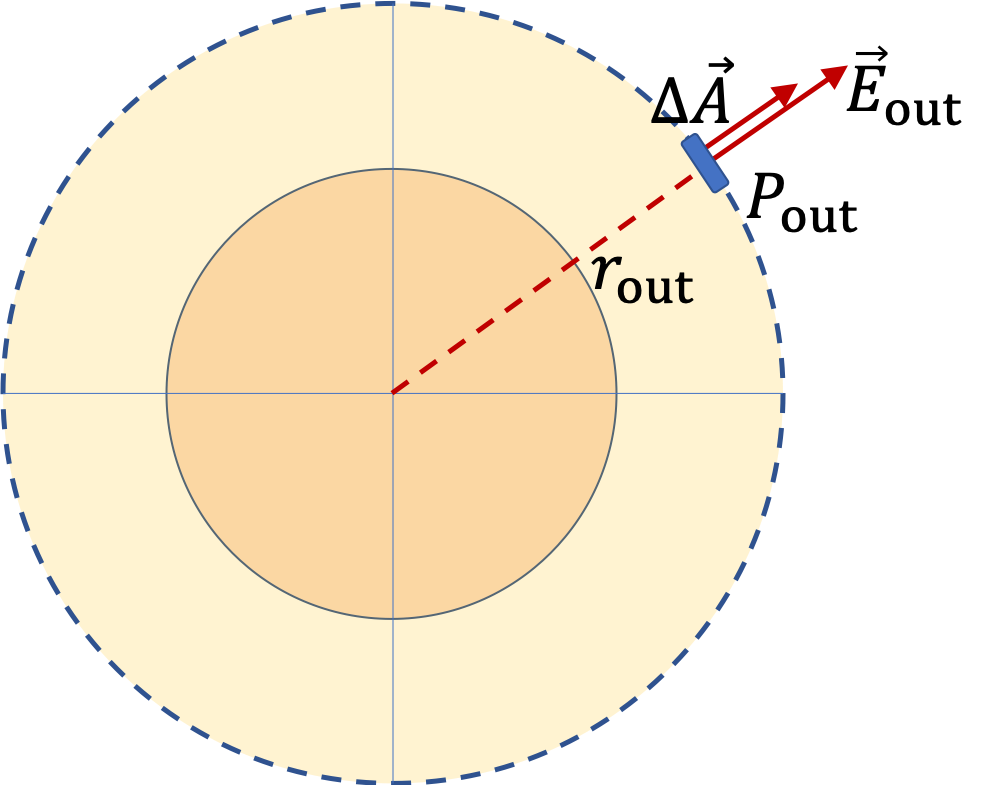
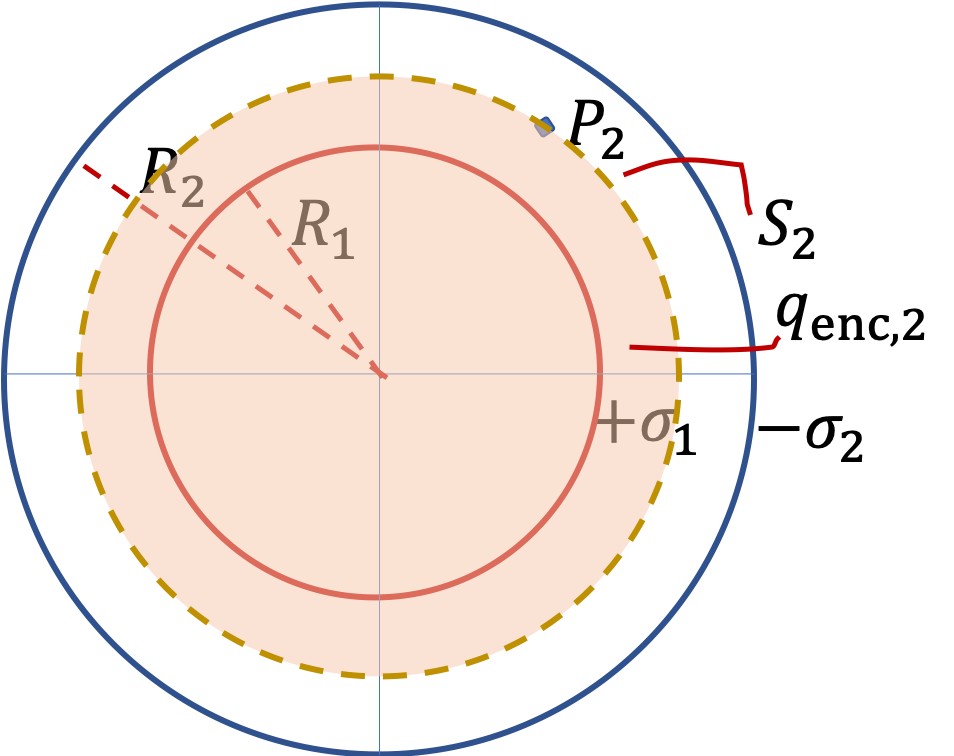
So, if we want field at one of these points, say \(P_3\text{,}\) we will imagine a spherical Gaussian surface \(S_3\) that contains point \(P_3\text{.}\) By spherical symmetry we already know the direction of \(\vec E_3\) and the magnitude will depend on charges inside the Gaussian closing surface, which we denote by \(q_\text{enc,3}\text{.}\)
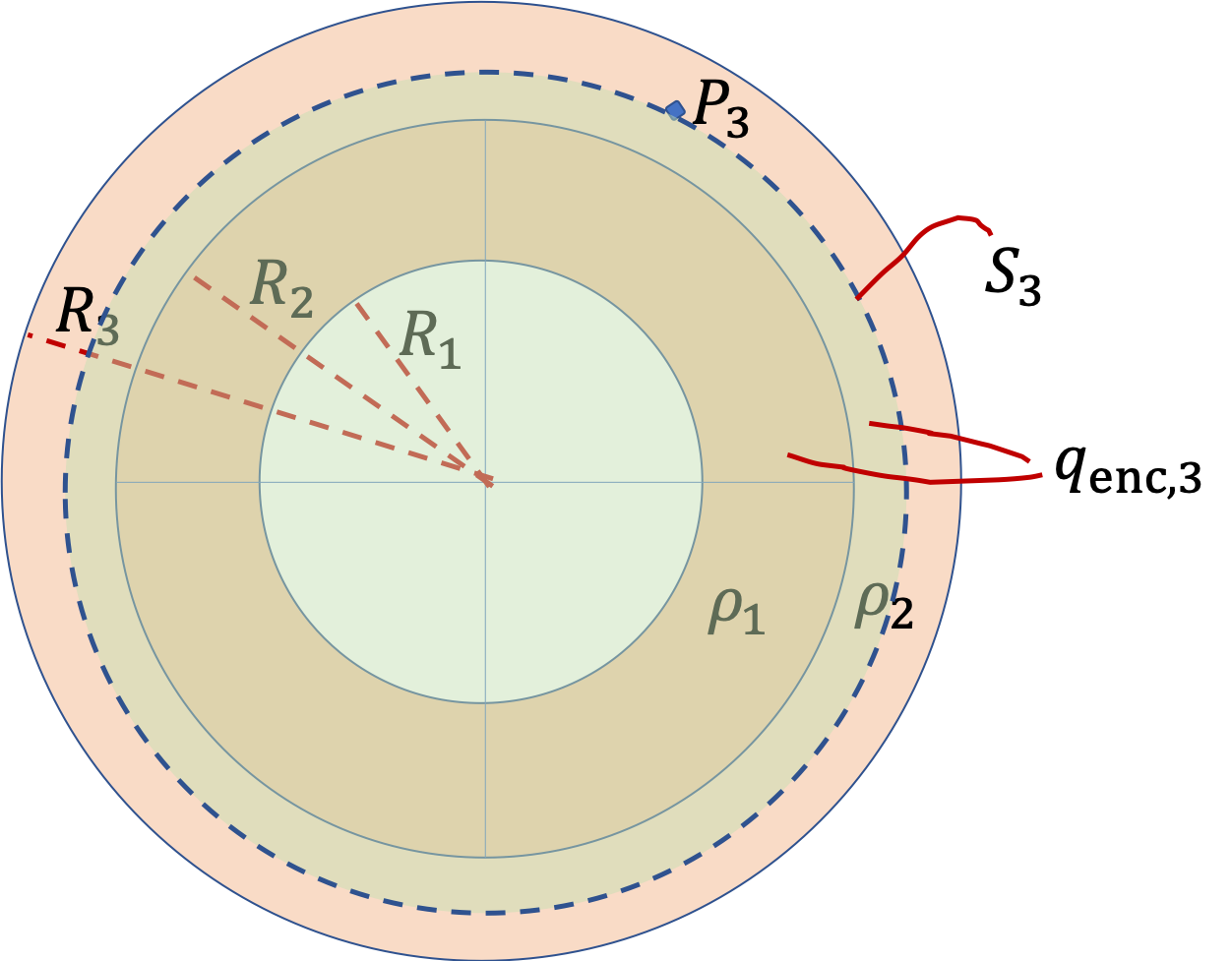
\begin{equation*}
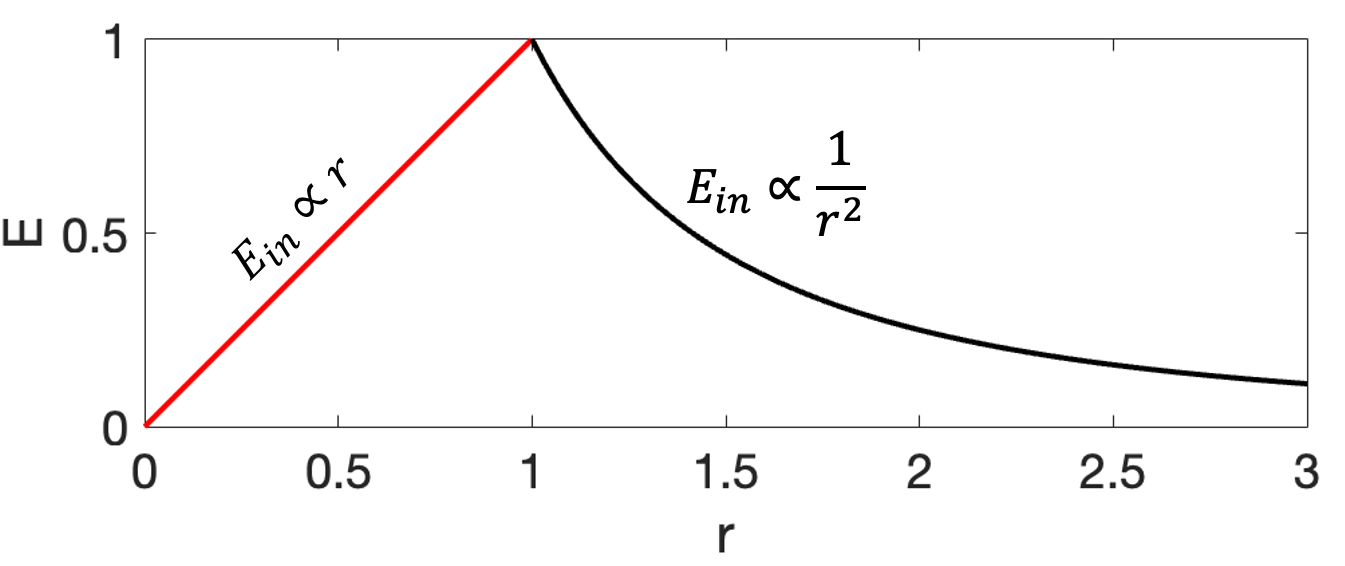
E_3 = \dfrac{1}{4\pi\epsilon_0}\, \dfrac{q_\text{enc,3}}{r_3^2}.
\end{equation*}
Same arguments can be applied at all four points. Let us denote the distances to the field points from the common center be \(r_1\text{,}\) \(r_2\text{,}\) \(r_3\text{,}\) and \(r_4\text{.}\) So, the only thing we need to work out the enclosed charges in each case.
\begin{align*}
q_\text{enc,1} \amp = 0, \\
q_\text{enc,2} \amp = \rho_1\, \dfrac{4}{3}\pi\left(r_2^3 - R_1^3 \right), \\
q_\text{enc,3} \amp = \rho_1 \, \dfrac{4}{3}\pi\left(R_2^3 - R_1^3 \right) + \rho_2\, \dfrac{4}{3}\pi\left(r_3^3 - R_2^3 \right), \\
q_\text{enc,4} \amp = \rho_1 \, \dfrac{4}{3}\pi\left(R_2^3 - R_1^3 \right) + \rho_2\, \dfrac{4}{3}\pi\left(R_3^3 - R_2^3 \right),
\end{align*}
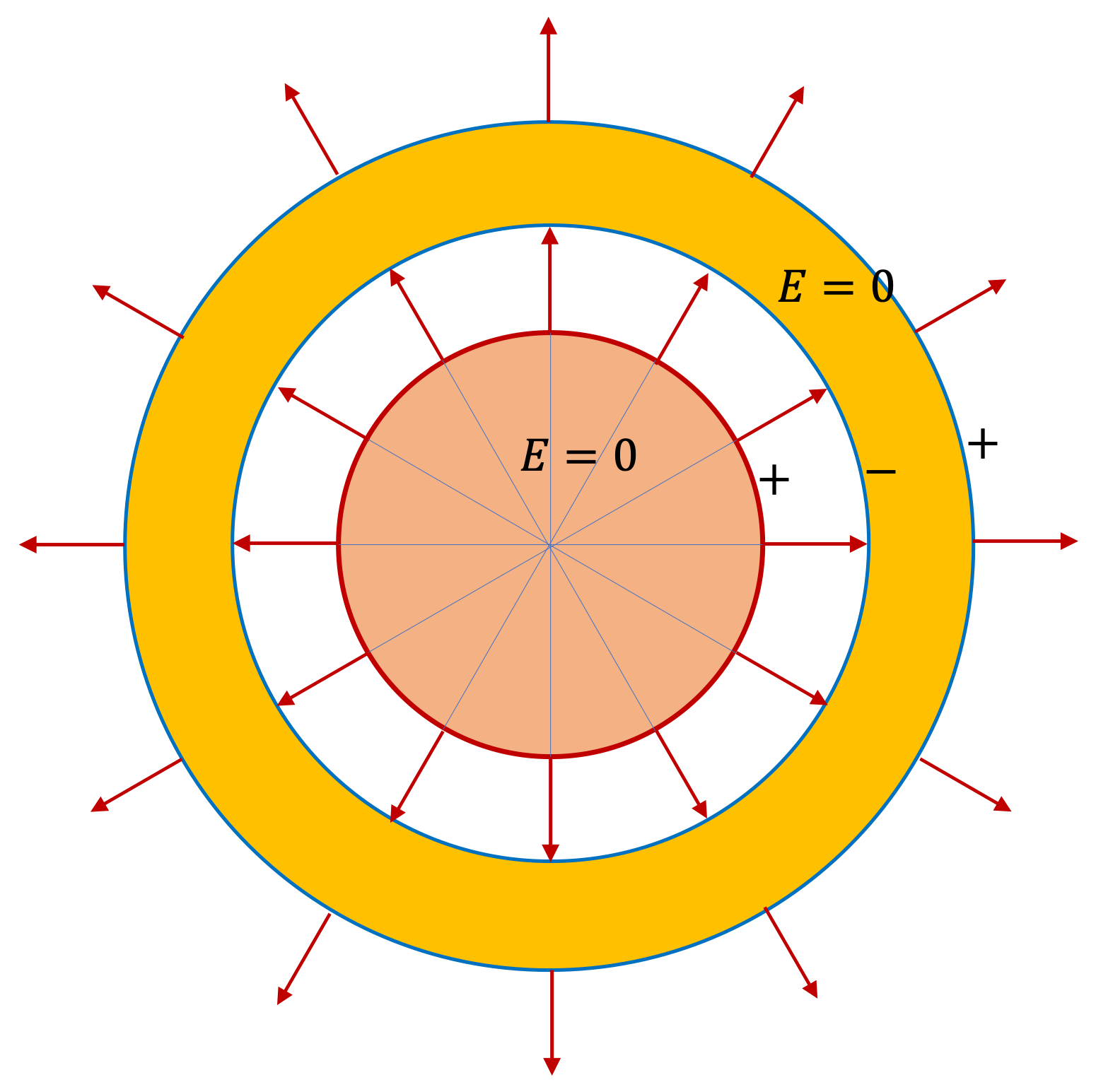
Therefore, electric fields are radial outward if \(q_\text{enc,i}\) is positive and radially inward if \(q_\text{enc,i}\) is negative, and the magnitude will be
\begin{equation*}
E_i = \dfrac{1}{4\pi\epsilon_0}\, \dfrac{q_\text{enc,i}}{r_i^2}.
\end{equation*}
for \(i=1,\ 2,\ 3, 4\text{.}\)