Drag Force

Section 6.14 Drag Force

Drag force is the force that a fluid applies on a moving body in the fluid. This type of friction is different from kinetic friction between solids in one important way: while the kinetic friction did not depend much on the speed of the object, the drag force depends on the speed.

Drag force occurs through two mechanisms:

viscous drag force: due to viscous flow of the fluid around the body of the fluid.
inertial drag force: due to pushing of the fluid out of the way from in front of the moving body.

While both of these drag forces act on a moving body, often one of them is highly dominant in a particular situation. For instance, if the body is moving very fast, the inertial drag force will be the dominant force and when the body is moving slowly in a viscous fluid, the viscous force will be the dominant component. We will address both of these drag forces below.

Our treatment of drag force will give you a very simplified picture of what is actually goes on when an object is moving in a fluid. A fuller treatment of the subject is quite complicated and beyond the scope of this book. However, our treatment will give you sufficient understanding of the physics involved for you to be able to address the role of viscous forces in many practical situations. We will also study viscosity in the chapter on dynamic fluid.

Subsection 6.14.1 Viscous Drag Force

Viscous drag force occurs due to forces between the molecules of the fluid. Due to the attractive nature of these forces, molecules tend to stick to each other. When a body is moving in a fluid, the molecules of the fluid next to the body will move with the velocity of the body, but molecules further away would not move much or at all. Thus, at low speeds you find layers of fluid moving past each other, causing a laminar flow as shown in Figure 6.60.

The magnitude of the drag force is proportional to one power of speed if body is moving “slowly” so that a laminar flow of fluid around the object occurs as shown in Figure 6.60. In this range of speed, the drag is dominated by viscous effects of the fluid. Sir George Stokes published in 1840s a formula for the viscous drag force on a moving sphere of radius \(R\text{.}\)

\begin{equation} F_{D}^{\text{viscous}} = 6\pi\eta R\, v,\tag{6.22} \end{equation}

where \(v\) is the speed of sphere and \(\eta\) viscosity of the fluid.

The formula in Eq. (6.22) is called Stoke’s force, linear drag force or viscous drag force. For other shapes, you might think that the general formula may be written as

\begin{equation*} F_{D}^{\text{viscous}} = k\,\eta\, v, \end{equation*}

where \(k\) will be shape-dependent with dimension of length. The direction of viscous drag force is, just like the kinetic friction, in the opposite direction of the velocity of the moving object.

Subsection 6.14.2 Inertial Drag Force

If a body is moving rapidly through a fluid, the flow of the fluid around the object is no longer laminar. In these cases, the fluid becomes turbullent. This is the case, for instance, when you drop a steel ball in air. The resistive force of the fluid is mainly as a reaction to the impulse on the fluid by the moving ball, hence, it is known as inertial drag force.

Suppose a spherical ball is moving through a fluid at speed \(v \) as shown in Figure 6.61. From the perspective of the ball, i.e., in the ball frame, the fluid in front of the ball would be striking the ball at speed \(v \text{.}\)

When the moving molecule hits the ball, it must come to rest. Net effect is the change in momentum of the fluid which is transfered to the change in momentum of the ball. In one second, fluid will deposit a momentum equal to

\begin{equation} \Delta p = \text{Volume}\times \text{Density} \times v,\tag{6.23} \end{equation}

where Volume is the volume in front of the ball of a cylinder of cross-section equal to the cross-section of the ball, i.e., here \(\pi R^2\text{,}\) and the height equal to \(v\text{,}\) since in one second, all the fluid up to this distance would have hit the ball.

Writing \(\rho \) for the density of the fluid, we find the following for the rate at which momentum is deposited by the fluid on the ball in the opposite direction to the fluid flow.

\begin{equation*} \dfrac{\Delta p}{\Delta t} = \pi R^2 \rho v^2. \end{equation*}

We usually write a more general formula that can apply to other shapes.

\begin{equation*} \dfrac{\Delta p}{\Delta t} = \dfrac{1}{2}\,C_D\, A\, \rho\, v^2, \end{equation*}

where \(A \) is the frontal area of cross-section of the moving object that is blocking the fluid flow past the body, and \(C_D \) the drag coefficient. The rate of change of momentum acts as a resistive force. It is called the inertial drag force.

\begin{equation} F_{D}^{\text{inertial}} = \dfrac{1}{2}\,C_D\, A\, \rho\, v^2. \tag{6.24} \end{equation}

The drag coefficient \(C_D\) is a dimensionless number that depends on shape and speed in a complicated way, usually determined experimentally. But, for most systems, the value os between \(0.4\) and \(1.0\text{.}\) To get a sense of ballpark value of drag, you may just set it to \(1.0\text{.}\) In problems in books, \(C_D\) is normally specified with the problem or you could lok up in a table such as Table 6.62, so you don’t need to worry about it.

From the formula for the inertial drag in (6.24), you can see that, to reduce drag, you could reduce the area \(A\) that the body presents in the way of the flow. This parameter plays important role in the design of cars and airplanes for drag reduction. Skiers and skydivers also manage drag on their bodies by crouching and changing shape effectively changing \(A\text{.}\)

Table 6.62. Representative \(C_D \) Values. The values in the table are from wikipedia sources. A good resource: https://www.engineeringtoolbox.com/drag-coefficient-d_627.html

Object	\(C_D \)
Smooth sphere	\(0.47 \)
Car	\(0.25 \)
Skier	\(1.0 - 1.1 \)
Boeing 787	0.024
Dophin	0.0036

Subsection 6.14.3 Reynold’s Number

Shoud I use \(F_{D}^{\text{viscous}}\) or \(F_{D}^{\text{inertial}} \text{?}\) Since both drags are present all the time, we need to see if we need to use both or if one of them is extremely dominant. A ratio of the inertial drag to viscous drag could be used to test how big one is compared to the other. For a spherical ball, we get

\begin{equation*} \dfrac{F_D^{\text{inertial}}}{F_D^{\text{viscous}}} = \dfrac{C_D}{12} \dfrac{\rho R v}{\eta}. \end{equation*}

Rather than this formukla, we actually use a related dimensionless quantity, called Reynold’s number, defined by

\begin{equation*} N_R = \dfrac{2R\, \rho\, v}{\eta}, \end{equation*}

In general, we replace \(2R \) by a suitable measure of a length scale \(L \) of the moving object that is being pushed against by the fluid flow.

\begin{equation} N_R = \dfrac{L\, \rho\, v}{\eta},\tag{6.25} \end{equation}

The rule of thumb is that if \(N_R \gt\gt 1 \text{,}\) use the inertial drag, and, if \(N_R \lt\lt 1 \) use the simpler linear drag, otherwise use the sum of the two.

Subsection 6.14.4 Terminal Speed

Consider an object falling in air or some fluid. Initially speed is too small and gravity dominates. That leads to increasing speed in the fall. Now, suppose that the object can present significant area \(A\) to the fluid so that inertial drag force on it is considerable once speed has picked up. If the height by which the object has fallen, at some point in the fall its speed would be such that the upward inertial drag force would balance the force of gravity. At that point onward, the forces on the object will be balanced and no further increase in speed would occur. This speed is called terminal speed. Using Eq. (6.24), we can find a general expression for terminal speed, \(v_t\) by setting the inertial drag force for \(v=v_t\) to the weight of the body gives

\begin{equation*} \dfrac{1}{2}\,C_D\, A\, \rho\, v_t^2 = m g. \end{equation*}

Therefore,

\begin{equation} v_t = \sqrt{ \frac{2mg}{C_D\, A\, \rho} }.\tag{6.26} \end{equation}

For a human body, let \(C_D=0.5\text{,}\) \(m=65.0\text{ kg}\text{,}\) \(A = 1.5\text{ m} \times 0.4\text{ m} = 0.6\text{ m}^2\text{,}\) in air, \(\rho=1.225\text{ kg/m}^{3}\text{.}\) This will give terminal speed to be

\begin{equation*} v_t = \sqrt{ \frac{2\times 65 \times 9.81}{0.5 \times 1.5\times 1.225} } = 37.3\text{ m/s}. \end{equation*}

With parachute, you may increase the area. Say, you make the area \(4\times\text{.}\) Then, you will cut down \(v_t\) by \(2\times\text{,}\) i.e., \(v_t\) now will be \(18.65\text{ m/s}\text{.}\)

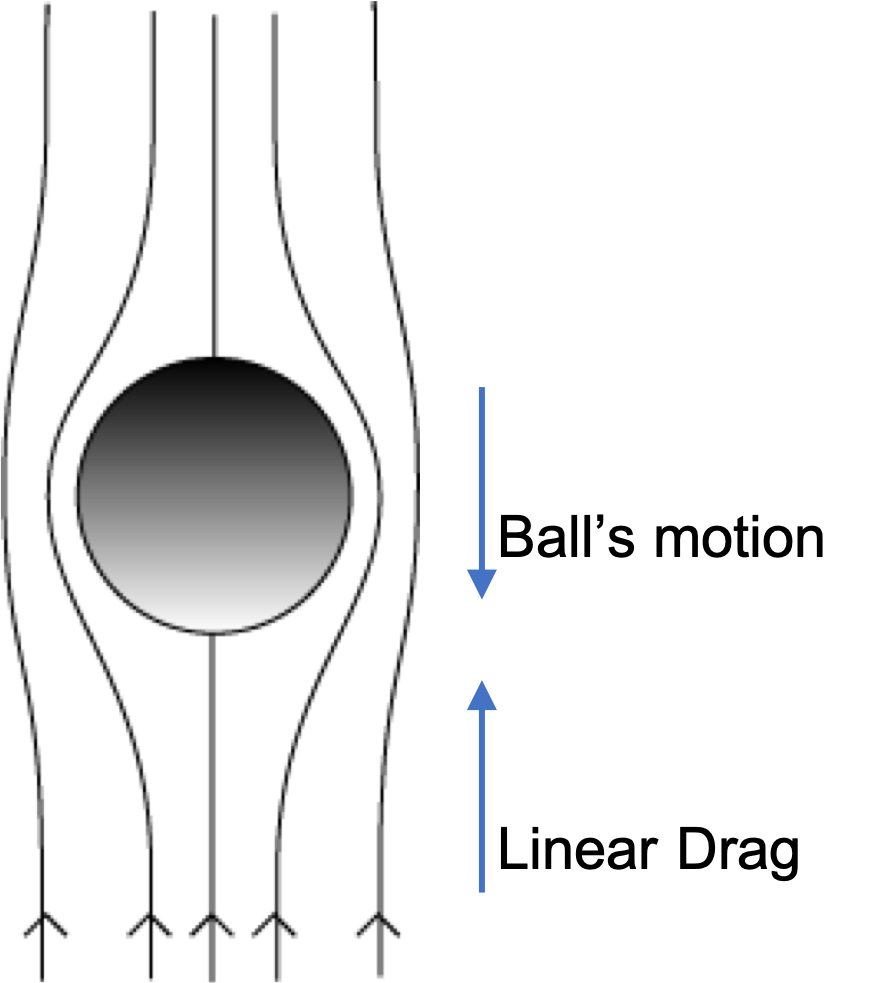
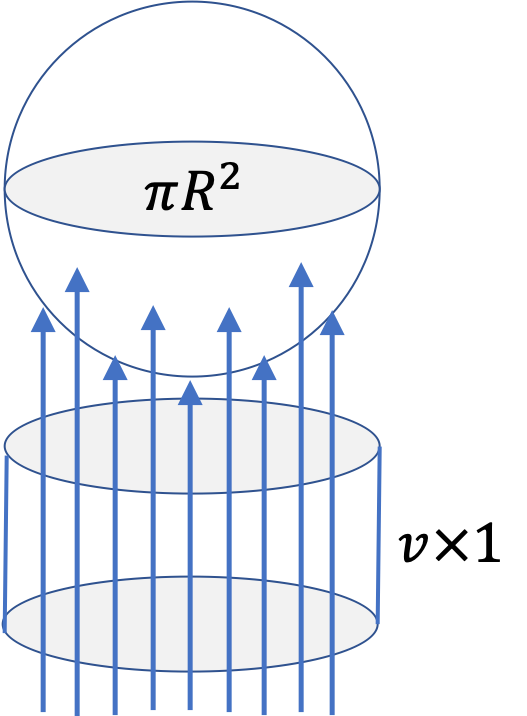
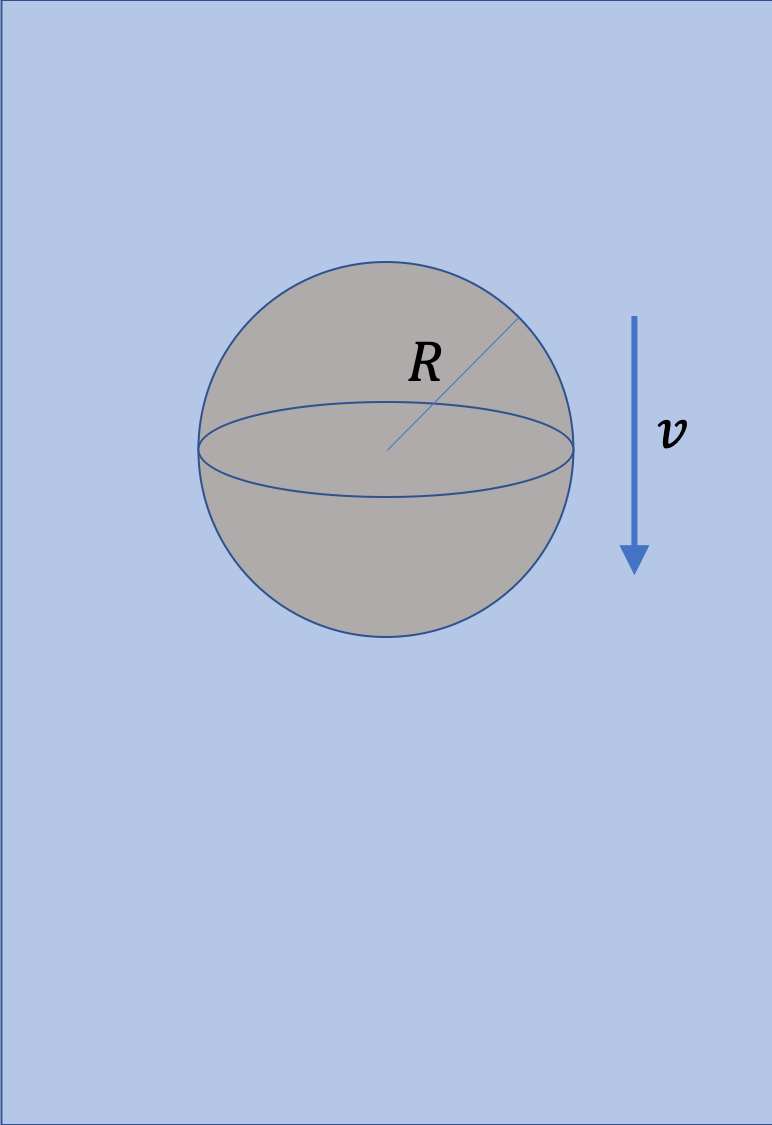
Example 6.63. Computing Viscous Drag Force Given the Speed.

An amoeba is moving in water at speed \(10\, \mu\text{m/min}\text{.}\) You can assume amoeba to be a sphere of radius \(500\, \mu\text{m}\text{.}\)

(a) What is the Reynold’s number of the fluid flow at the speed of the amoeba? Decide which drag force is dominant here.

(b) Based on your decision in (a), compute the drag force on the amoeba.

Data: Viscosity \(\eta \) of water to be \(0.009\text{ Pa.s}\) and the density of water to be \(1000\text{ kg/m}^3\text{.}\)

Answer.

(a) \(1.9\times 10^{-5}\text{,}\) (b) \(1.41\times 10^{-11}\text{ N} \text{,}\)(c) \(364,300\text{.}\)

Solution 1. a

We use the formula for the Reynold’s number to find the value. In the Reynold’s number formula, we need to choose a length scale for the moving object, for which we choose the diameter of amoeba as tthe relevant length scale. We also convert all the units in the standard SI units of \(\text{m, s, kg}\text{.}\)

\begin{align*} N_R \amp = \dfrac{L \rho v }{\eta}, \\ \amp = \dfrac{2\times 500\times 10^{-6} \times 1000\times \frac{1}{6}\times 10^{-6}}{ 0.009} = 1.9\times 10^{-5}. \end{align*}

This says that viscous drag will be the dominant one for amoeba.

Solution 2. b

We can make a drastic assumption and assume amaeba to have a spherical shape. This is just to get a ballpark answer. Using the formula for the viscous drag force for a sphere, we find

\begin{align*} F_D^{\text{viscous}} \amp = 6\pi\eta R v, \\ \amp = 6\times \pi \times 0.009\times 500\times 10^{-6} \times \frac{1}{6}\times 10^{-6}\\ \amp = 1.41\times 10^{-11}\text{ N}. \end{align*}

Solution 3. c

To find the weight of amoeba, we need to find its mass. We will get its mass by multiplying its volume by the density.

\begin{equation*} \text{Volume, }V = \dfrac{4}{3}\pi R^3 = 5.24\times 10^{-10}\, \text{m}^3. \end{equation*}

Therefore, weight of the amoeba is

\begin{equation*} W = mg = \left( 1000 * 5.24\times 10^{-10} \right) * 9.81 = 5.14\times 10^{-6}\text{ N}. \end{equation*}

Comparing drag to weight we get.

\begin{equation*} \dfrac{W}{F_D} = \dfrac{5.14\times 10^{-6}}{1.41\times 10^{-11}} = 364,300. \end{equation*}

Example 6.64. Computing Inertial Drag Force.

Inertial drag force is important at high speeds. A dolphin is swimming in water at a speed of \(10 \text{ m/s}\text{.}\) Model the dolphin as a cylinder of radius \(0.5\text{ m} \) and length \(4\text{ m}\text{.}\)

(a) Find the Reynold’s number for the water flow at the speed of the dolphin.

(b) Based on the Reynold’s number, decide if you should omit the viscous drag and only use the inertial drag when computing the drag force, and then find the drag force on the dolphin.

Data: Viscosity \(\eta \) of water is \(0.009\text{ Pa.s}\text{.}\) You may use the drag coefficient of dolphin to be \(C_D = 0.0036\text{.}\) Density of water = \(1000\text{ kg/m}^3\text{.}\)

Answer.

(a) \(1.0 \times 10^6\) ,(b) \(141.4\text{ N}\text{,}\) (c) \(35.4\text{ N}\text{.}\)

Solution 1. a

We use the formula for the Reynold’s number to find the value. In the Reynold’s number formula, we need to choose a length scale for the moving object, for which we choose the diameter of the cylinder modeling the dolphin since that is the size which is perpendicular to the flow.

\begin{align*} N_R \amp = \dfrac{L \rho v }{\eta}, \\ \amp = \dfrac{ 2\times 0.5 \times 1000\times 10 }{ 0.009} = 1.0 \times 10^6. \end{align*}

Solution 2. b

Since \(N_R \gt\gt 1 \text{,}\) the inertial drag is way more than the viscous drag. Therefore, we drop the viscous drag. Using the formula for the inertial drag force, we find

\begin{align*} F_D^{\text{inertial}} \amp = \dfrac{1}{2}\,C_D A \rho v^2, \\ \amp = 0.5\times 0.0036\times \pi\times 0.5^2\times 1000\times 10^2 = 141.4\text{ N}. \end{align*}

Solution 3. c

Since \(F_D \sim v^2 \text{,}\) if \(v \rightarrow \dfrac{v}{2} \text{,}\) \(F_D \rightarrow \dfrac{F_D}{4} \text{.}\) That is, the drag force will become one quarter.

\begin{equation*} F_D = \dfrac{141.4\text{ N}}{4} = 35.4\text{ N}. \end{equation*}

Example 6.65. Drag Force and the Terminal Velocity.

A steel ball of radius \(2.0\text{ cm}\) is gently placed inside a tube of water and released from rest. Initially, the ball accelerates but after some time reaches a terminal velocity, i.e., velocity does not change.

Data: Viscosity \(\eta \) of water is \(0.009\text{ Pa.s}\text{.}\) You may use the drag coefficient of sphere to be, \(C_D = 0.5\text{.}\) Density of steel = \(8000\text{ kg/m}^3\text{.}\) Density of water = \(1000\text{ kg/m}^3\text{.}\)

(a) Assuming viscous drag force to be the only drag force, find the speed at which the net force on the ball is zero. This assumption turns out to be incorrect for this situation, but we will discover that in part (b) below.

(b) What is the Reynold’s number of the flow at the terminal speed you found by assuming viscous drag as total drag in (a)? Decide if ignoring the inertial drag force was justified.

(c) You will find that viscous drag force is not the dominant drag force at this speed. We should be using the inertial drag force instead. Now, find the terminal velocity using the inertial drag force.

Answer.

(a) \(774\text{ m/s}\) ,(b) \(3,440,000\text{,}\) (c) \(2.9\text{ m/s} \text{.}\)

Solution 1. a

Using the formula for the viscous drag force, we find

\begin{align*} F_D^{\text{viscous}} \amp = 6\pi\eta R v, \\ \amp = 6\times \pi \times 0.009\times 0.02 \times v = 0.0034\, v. \end{align*}

This must balance the weight for acceleration to be zero. We need to find the mass of the ball to find the weight. We will get that from the volume \(V \) of the ball and the density of steel.

\begin{align*} V \amp = \dfrac{4}{3}\pi R^3, \\ \amp = \dfrac{4}{3}\times \pi \times 0.02^3 =3.35\times 10^{-5}\text{ m}^3. \end{align*}

Therefore,

\begin{equation*} W = mg = (3.35\times10^{-5}\times 8000)\times 9.81=2.63\text{ N}. \end{equation*}

Balancing this with the viscous drag gives

\begin{equation*} 0.0034\, v = 2.63\ \ \Longrightarrow\ \ v = 774\text{ m/s}. \end{equation*}

Solution 2. b

\begin{align*} N_R \amp = \dfrac{L \rho v }{\eta}, \\ \amp = \dfrac{ 0.04 \times 1000\times 774 }{ 0.009} = 3,440,000. \end{align*}

This is saying that at this speed, the inertial drag is 3,440,000 times more important. That means, our terminal speed calculated in (a) is wrong. We should, instead, use the inertial drag formula.

Solution 3. c

Using the formula for the inertial drag force, we find

\begin{align*} F_D^{\text{inertial}} \amp = \dfrac{1}{2}C_D A \rho v^2, \\ \amp = 0.5\times 0.5\times \pi\times 0.02^2\times 1000\, v^2 = 0.315\, v^2. \end{align*}

This must balance the weight for acceleration to be zero. We found weight in part (a). Now, we get the following equaiton for \(v \text{.}\)

\begin{equation*} 0.315\, v^2 = 2.63\ \ \Longrightarrow\ \ v = 2.9\text{ m/s}. \end{equation*}

Thus, the terminal velocity for the steel ball is \(2.9\text{ m/s}\text{.}\) This is a much more reasonable number than the wrong value of terminal speed found in (a).

Exercises 6.14.5 Exercises

1. Comparison of Inertial Drag Forces on Two Airplanes.

A commercial airliner is cruising with speed 600 mph at an altitude of 40,000 feet. When it took off, it had a speed of 150 mph. The density of air is \(1.22\text{ kg/m}^3\) near ground and \(0.385\text{ kg/m}^3\) at 40,000 ft. Compare the inertial drag force on the airplane in the two situations.

Hint.

No need to convert units. Work with ratio.

Answer.

Near ground : at 40,000 ft = \(0.2\text{.}\)

Solution.

Let \(F_\text{d0}\) and \(F_\text{d4}\) be drag forces on ground and at 40,000 ft. Using Eq. (6.24) will be

\begin{align*} \frac{F_\text{d0}}{F_\text{d4}} \amp = \frac{\dfrac{1}{2}\,C_D\, A\, \rho_0\, v_0^2}{\dfrac{1}{2}\,C_D\, A\, \rho_4\, v_4^2} = \frac{ \rho_0\, v_0^2}{ \rho_4\, v_4^2} \end{align*}

We do not need to do any conversion of units since the ratio of similar quantities will cancel out the units.

\begin{equation*} \frac{F_\text{d0}}{F_\text{d4}} = \frac{ 1.22}{0.385} \times \left( \frac{150}{600} \right)^2 = 0.2. \end{equation*}

2. (Calculus) Speed and Distance of a Skier with Inertial Drag Force.

A \(70\text{-kg}\) skier glides down a “frictionless” slope starting from rest on a flat incline with angle of inclination \(\theta=30^\circ\text{.}\) The motion of skier is impeded by inertial drag force from air. Suppose \(C_D=0.4\) and \(\rho_\text{air}=1.22\text{kg /m}^3\text{,}\) and the skier presents and area of \(A=1.2\text{ m}^2\text{.}\) (a) Find the terminal speed of the skier. (b) Find the expression of speed \(v\) as a function of time \(t\) with \(t=0\) at start where \(v=0\text{.}\) (c) Find the expression of distance on the slope the skier travels in time \(t\text{.}\)

Hint.

(a) Set up the condition for zero acceleration. (b) Write \(F_x = m dv_x/dt\) and solve for \(v_x\text{.}\) (c) Integrate the result of (b).

Answer.

(a) \(34.2\text{ m/s}\text{,}\) (b) \((34.3\text{ m/s})\; \tanh( 0.143\; t)\text{,}\) (c) \((239\text{ m}) \ln( \cosh( 0.143\; t ) )\text{.}\) You might different expressions for (b) and (c) since the integrals can be written in other forms also.

Solution 1. (a)

(a) Figure 6.67 shows three forces acting on the skier. Let \(v_x\) and \(a_x = dv_x/dt\) denote the \(x\) component of velocity and acceleration respectively. Equation of motion \(F_x = m a_x= m dv_x/dt\) will be

\begin{equation} m \frac{dv_x}{dt} = m g \sin\theta - \frac{1}{2} C_D \rho A v_x^2.\tag{6.27} \end{equation}

When speed is terminal speed \(v_t\text{,}\) then, it has zero acceleration. This gives

\begin{equation*} v_t = \sqrt{ \frac{2 m g \sin\theta}{ C_D \rho A } }. \end{equation*}

Putting the numerical values we get

\begin{equation*} v_t = \sqrt{ \frac{2 \times 70 \times 9.81 \times \sin\, 30^\circ}{ 0.4 \times 1.22 \times 1.2 } } = 34.2\text{ m/s}. \end{equation*}

Solution 2. (b)

Now, we work with the equation of motion, Eq. (6.27).

\begin{equation*} m \frac{dv_x}{dt} = m g \sin\theta - \frac{1}{2} C_D \rho A v_x^2. \end{equation*}

Let’s divide by \(m\) and replace myriad constants by symbols.

\begin{equation} \frac{dv_x}{dt} = a - b v_x^2,\tag{6.28} \end{equation}

where

\begin{equation*} a = g \sin\theta,\ \ \ b = \frac{1}{2m} C_D \rho A. \end{equation*}

Note that \(v_t = \sqrt{a/b}\text{.}\) Rearrange Eq. (6.28) and integrate from \(t=0\) to \(t\text{.}\)

\begin{equation*} \int_0^v \frac{d v_x}{ a - b v_x^2 } = \int_0^t dt. \end{equation*}

This gives (with \(v_t = \sqrt{a/b}\)):

\begin{equation} v = v_t \tanh(b v_t t ).\tag{6.29} \end{equation}

Now, using the numerical values we get

\begin{equation*} v = (34.3\text{ m/s})\; \tanh( 0.143\; t). \end{equation*}

Solution 3. (c)

Now, we integrate Eq. (6.29) to get the distance \(\Delta x\) on the slope.

\begin{equation*} \Delta x = \int_0^t v dt = \int_0^t v_t \tanh(b v_t t ) dt. \end{equation*}

This gives

\begin{equation*} \Delta x = \frac{1}{b} \log( \cosh( b v_t t ) ). \end{equation*}

Now, using the numerical values we get

\begin{equation*} \Delta x = (239\text{ m}) \ln( \cosh( 0.143\; t ) ). \end{equation*}

3. (Calculus) Practice with a Friend: Accounting for Air Drag on a Bob Sled.

A bob sled with riders weighing \(500\text{ kg}\) starts at rest and comes down a straight incline of length \(100\text{ m}\) at angle \(12.5^\circ\) with the horizon. The coefficient of kinetic friction between the sled and the ground is \(0.15\text{.}\) The bob sled is also subject to inertial air drag with parameters \(C_D = 0.8\text{,}\) \(A=1.8\text{ m}^2\text{,}\) \(\rho_\text{air} = 1.22\text{ kg/m}^3\text{.}\) How long does it take the Bob sled to finish the \(100\text{ m}\) slide?

Hint.

See Exercise 6.14.5.2 with \(a\) there will change to \(g\sin\theta - \mu_k g \cos\theta\text{.}\)

Prev Top Next