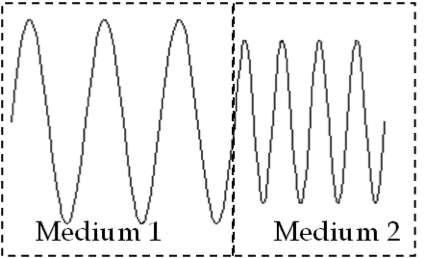
Example 43.20. Speed and Wavelength of Light in Glass.
Find speed and wavelength of light in glass if its wavelength in vacuum is \(632.8\text{ nm}\text{.}\) Use \(n = 1.55\) for the refractive index of glass for the given light.
Answer.
\(1.94\times 10^8\ \text{m/s}\text{,}\) \(408.3\ \text{nm}\text{.}\)
Solution.
We can find the value of speed easily by dividing the speed in vacuum by the refractive index.
\begin{align*}
v \amp = \frac{c}{n} = \frac{3\times 10^8\ \text{m/s}}{1.55}
= 1.94\times 10^8\ \text{m/s}.
\end{align*}
For the wavelength we note that frequency of light does not change when it passes from one medium into another. Let \(\lambda_0\) be the wavelength of the light in vacuum and \(\lambda\) be the wavelength of the same light in the medium. The, we will have
\begin{equation*}
f = \frac{c}{\lambda_0} = \frac{v}{\lambda}.
\end{equation*}
Since \(v = c/n\text{,}\) we obtain
\begin{equation*}
\lambda = \frac{\lambda_0}{n} = \frac{632.8\ \text{nm}}{1.55} = 408.3\ \text{nm}.
\end{equation*}