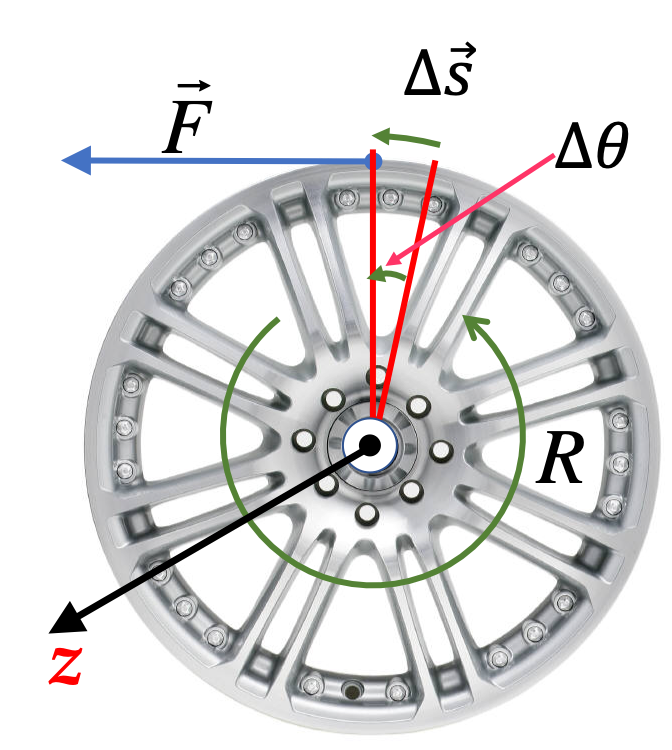
Example 9.124. Work in Tightening a Bolt.
A \(12\text{-inch}\)-long wrench is used to tighten a bolt by applying a steady force of \(5\text{ N}\) at the end of the handle which is approximately \(10\text{ inches}\) from the center of the bolt.
(a) How much work is done for each quarter turn?
(b) Suppose, you use a \(6\)-in wrench, and apply the same force, except that the force now would act at a distance of about \(5\text{ inches}\) from the center of the bolt. How much work would now be done for each quarter turn?
Answer.
(a) \(2.0\text{ N.m} \text{,}\) (b) \(1.0\text{ N.m}\text{.}\)
Solution 1. a
The lever arm of the \(5\text{ N}\) force is
\begin{equation*}
r_\perp = 10\text{ inches} \times 0.0254\text{ m/inch} = 0.254\text{ m}.
\end{equation*}
Therefore, the torque is
\begin{equation*}
\tau = 5\text{ N} \times 0.254\text{ m} = 1.28\text{ N.m}.
\end{equation*}
The angle to be rotated at this torque level is
\begin{equation*}
\Delta \theta = 0.25\text{ turn} \times 2\pi\text{ rad/turn} = \dfrac{\pi}{2}\text{ rad}.
\end{equation*}
Therefore, the rotational work is
\begin{equation*}
W_\text{rot} = \tau\Delta \theta = 2.0\text{ N.m}.
\end{equation*}
Solution 2. b
The lever arm of the \(5\text{ N}\) force is now half as much. This factor will continue into the work.
\begin{equation*}
W_\text{rot} = 1.0\text{ N.m}.
\end{equation*}