Position

Section 4.1 Position

Position is a vector from a reference object or reference point in space to the location of the object. Usually, coordinate system for the study is chosen so that its origin is at th location of the reference object or the reference point in space. We will denote position vector by \(\vec r \text{.}\)

Figure 4.1 shows position vector and a three-dimensional coordinate system. The arrow from origin O to point P represents the vector pictorially. The coordinates \((x,y,z) \) are the Cartesian components of vector \(\vec r\text{.}\) The direct distance OP, i.e., the length of the vector \(\vec r \text{,}\) is magnitude of the vector. The spherical coordinate angles \(\theta \) and \(\phi \) can be used to indicate the direction of vector \(\vec r \) in the three-dimensional space.

Figure 4.1. Position vector \(\vec r \) for a particle located at P. Point Q in the \(xy\)-plane is the point where normal from point P intersects the \(xy\)-plane.

In a two-dimensional space, say in the \(xy\) plane, position vector would be as vector from O to P, where P is now in the \(xy\) plane. In this case, we need only angle \(\theta \) from \(x \) axis to describe the direction as shown in Figure 4.2.

In one dimensions, say motion on \(x\) axis, direction is given by whether the location is on the positive side of origin or the negative side.

Figure 4.2. Position vector \(\vec r \) for a particle located at P in \(xy\) plane.

Subsection 4.1.1 Position Vector in the Component Form

The Cartesian components of the position vector \(\vec r\) are simply the Cartesian coordinates \((x, y, z)\) of the location. For some other vectors, e.g., a force vector \(\vec F\text{,}\) they would be denote by \((F_x, F_y, F_z) \text{.}\) If you compare the notations for components for vectors \(\vec r\) and \(\vec F\text{,}\) you might see that we are using \(r_x = x,\ r_y = y,\ r_z = z\text{,}\) but we do not write \((r_x, r_y, r_z) \text{.}\) While we use the notation of placing subscripts to the symbol of the vector, for \(\vec r\text{,}\) we don’t do that; we just use \((x,y,z)\) for \(\vec r\text{.}\)

We can also write the position vector using the unit vectors along the axes, namely, \(\hat i \) (towards positive \(x\)-axis), \(\hat j\) (towards positive \(y\)-axis), and \(\hat k\) (towards positive \(z\)-axis). That is, there are two equivalent ways of writing position vector (or any other vector) in terms of components.

\begin{equation} \text{Position Vector: } \vec r = (x, y, z) = x\hat i+ y \hat j + z \hat k.\tag{4.1} \end{equation}

Using unit vectors often makes it easier to do the algebra - clearly, it is another way of organizing the components of the vector.

Subsection 4.1.2 Magnitude and Direction of Position

Magnitude:

The magnitude of the position vector \(\vec r \) is simply the direct distance from the origin.

\begin{equation} \text{Magnitude of position vector, } r = \sqrt{x^2 + y^2 + z^2}.\tag{4.2} \end{equation}

Magnitude of vector in \(xy\) plane is similar. For direction of position in two and three dimensions, we proceed a little differently.

Direction of Vector in the \(xy\)-Plane:

If the vector is in the \(xy\)-plane, then we usually specify the angle of the vector with the \(x\)-axis as shown in Figure 4.2. Let \(\theta\) be the angle the vector makes with either the positive or the negative \(x \) axis directions, then by trig you can get

\begin{equation} \tan\, \theta = \dfrac{y}{x}.\tag{4.3} \end{equation}

Be aware that the value of this angle is not the direction of the vector. You need to interpret the value of \(\theta \) to deduce the direction. You can get the direction of the vector from the sign of \(\theta \) and the quadrant in which point \((x,y) \) lies. The situation in the four Cartesian coordinates is illustrated in Figure 4.3.

If \(\theta\) is positive, then the direction is obtained by going counter-clockwise from the axis, and if \(\theta\) is negative, then the direction is obtained by going clockwise from the axis, as seen from \(+z\) axis.
If \((x,y) \) is in first or fourth quadrant, the direction is with respect to the positive \(x \) axis, and if \((x,y) \) is in second or third quadrant, the direction is with respect to the negative \(x \) axis.

Figure 4.3. Position vector \(\vec r \) for a particle located at P in different quadrants in the \(xy\)-plane.

Direction of Vector in 3-Dimensions:

If the vector is in three-dimensions, for instance, the position of a star, we would need to specify two angles to describe the direction. One way to do that is familiar to you when you use the latitude and azimuth angles to locate places on the Earth. Another way is to give angles of the vector with the Cartesian axes. The easiest is perhaps the spherical angles as shown in Figure 4.1.

Spherical Angle Variables for Directions in 3-Dimensional Space. Spherical coordinates has two angles, the polar angle \(\theta \) between the vector and the positive \(z \) axis, and the azimuth \(\phi \) between the projection of the vector on the \(xy\) plane and the positive \(x \) axis. Note that \(\phi \) is not the direct angle between the vector and \(x \) axis but the angle of the projection. From the components \((x, y, z) \) these angles can be computed by the following formulas.

\begin{align} \amp \cos\,\theta = \dfrac{z}{r}, \tag{4.4}\\ \amp \tan\,\phi = \dfrac{y}{x}\tag{4.5} \end{align}

After computing, you would need to interpret the values vis-a-vis the octant the point \((x,y,z) \) lies.

Direction Cosines For Directions in 3-Dimensional Space. Let \(\theta_x, \theta_y, \theta_z\) be the angle that the position vector makes with the axes. These angles are often denoted by Greek letters \(\alpha, \beta, \gamma\text{,}\) respectively. By taking dot product of \(\vec r\) with \(\hat i\text{,}\) \(\hat j\text{,}\) and \(\hat k\text{,}\) we can show that

\begin{align} \amp \cos \theta_x = \dfrac{x}{r}\tag{4.6}\\ \amp \cos \theta_y = \dfrac{y}{r}\tag{4.7}\\ \amp \cos \theta_z = \dfrac{z}{r}\tag{4.8} \end{align}

These cosines are called direction cosines of the vector. It turns out that the three angles are not independent but are related by

\begin{equation} \cos^2 \theta_x + \cos^2 \theta_y + \cos^2 \theta_z = 1.\tag{4.9} \end{equation}

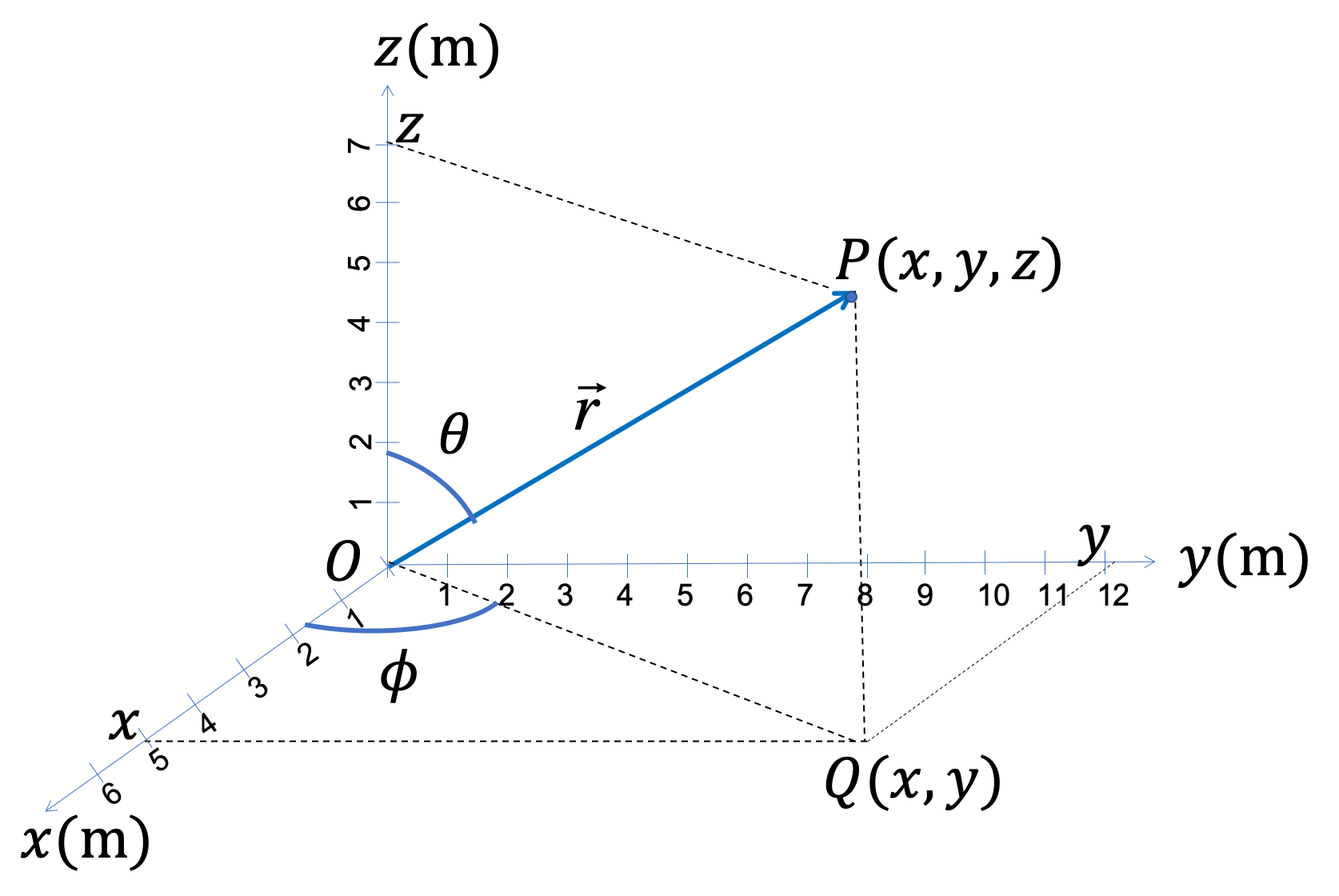
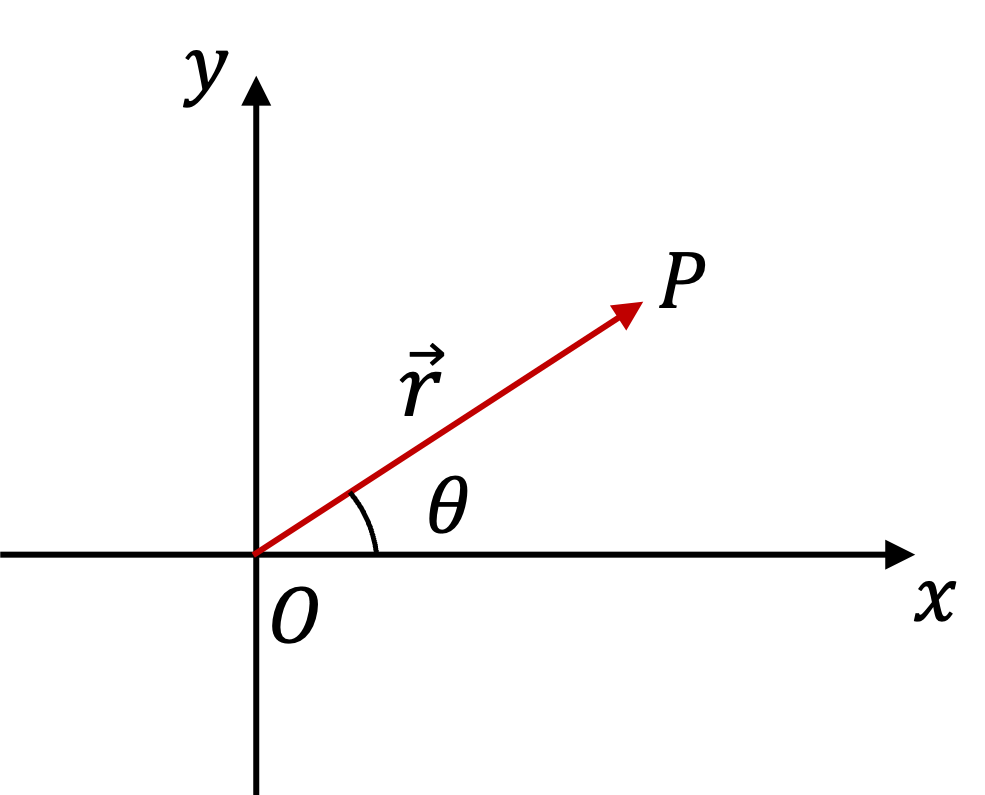
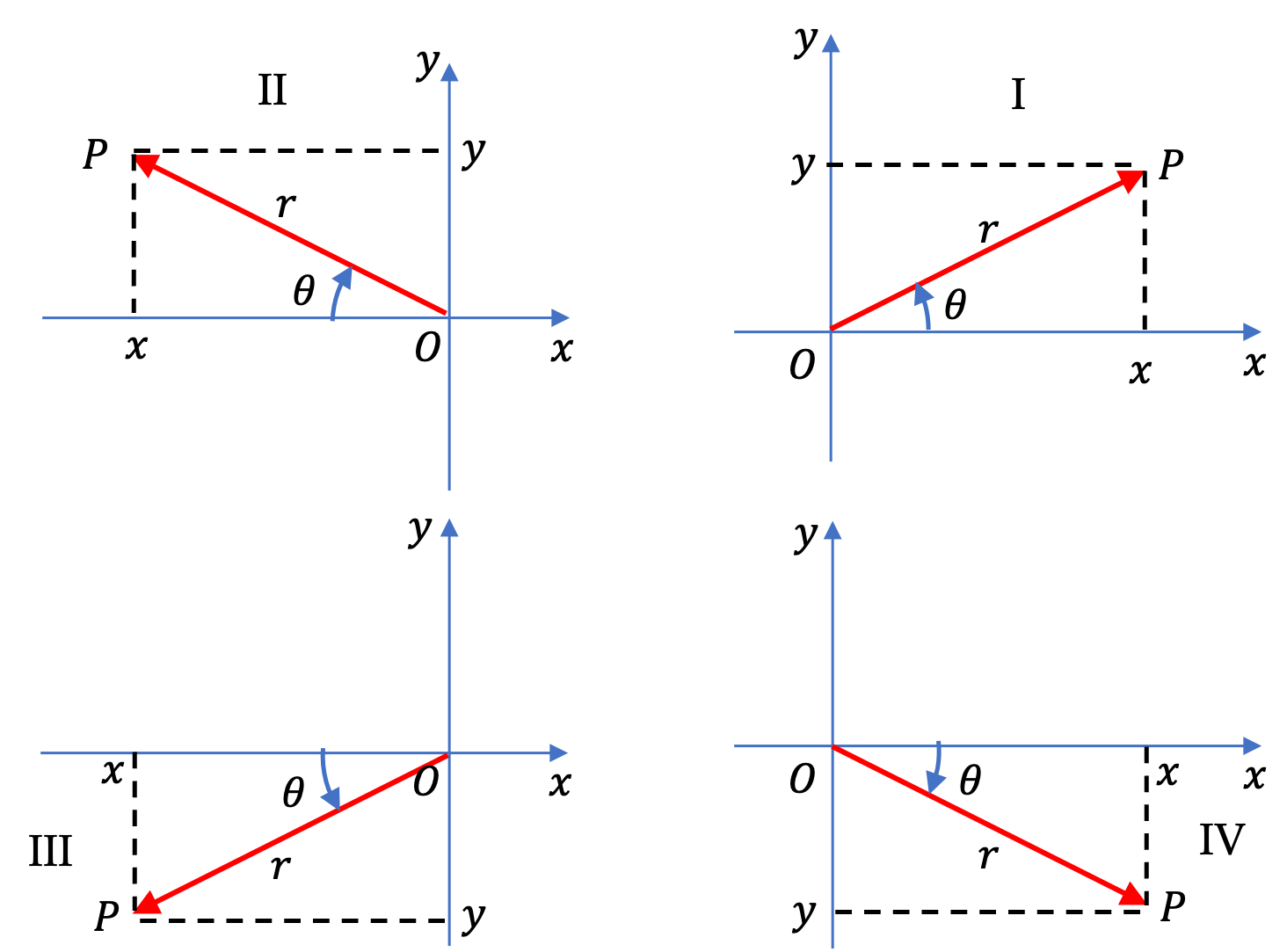
Example 4.4. Representations of a Position Vector in Plane.

A marble is located at a point in the \(xy\)-plane at the coordinates \((3 \text{ m}, 4 \text{ m}) \text{.}\) Express the position vector in (a) coordinate form, (b) magnitude-direction form, and (c) using unit vectors along the axes.

Answer.

(a) \((3 \text{ m}, 4 \text{ m}) \text{,}\) (b) \(5\text{ m} \text{,}\) \(53.1^{\circ} \) counterclockwise from the positive \(x \) axis, (c) \(3 \text{ m }\hat i + 4 \text{ m }\hat j\text{.}\)

Solution 1. a

The coordinate-form is already given in the problem statement as \((3 \text{ m}, 4 \text{ m}) \text{.}\)

Solution 2. b

Magnitude is:

\begin{equation*} r = \sqrt{x^2 + y^2} = \sqrt{3^2 + 4^2} = 5\text{ m}. \end{equation*}

First we find the angle \(\theta \) and then we interpret it to get the direction.

\begin{equation*} \theta = \tan^{-1}\left( 4/3 \right) = 53.1^{\circ}. \end{equation*}

Since the point \((3,4) \) is in the first quadrant, the direction is \(53.1^{\circ} \) counterclockwise from the positive \(x \) axis.

Solution 3. c

From the components in (a), we can immediately write

\begin{equation*} \vec r = 3 \text{ m }\hat i + 4 \text{ m }\hat j. \end{equation*}

Example 4.5. Three Dimensional Position Vector Magnitude and Direction Cosines.

The Cartesian coordinates of a person on the 10-th floor of a building is \((20 \text{ m}, 30\text{ m}, 35\text{ m}) \text{.}\) (a) How far away from the origin is the person? What is the angle the position vector of the person makes with (b) the \(x\) axis, (c) the \(y\) axis, and (d) with the \(z\) axis?

Answer.

(a) \(50.3\text{ m}\text{,}\) (b) \(66.6^{\circ}\text{,}\) \(53.4^{\circ}\text{,}\) \(45.9^{\circ}\text{.}\) (c) \(\theta_y = 53.4^{\circ}\text{,}\) (d) \(\theta_z = 45.9^{\circ}\text{.}\)

Solution 1. a

The distance is the radial distance of the spherical coordinate system.

\begin{equation*} r = \sqrt{20^2 + 30^2 + 35^2} = 50.3\text{ m}. \end{equation*}

Solution 2. b

The dot product between the given position and \(\hat i \) vector will give us the cosine of angle with the \(x \) axis.

\begin{equation*} \cos\, \theta_x = \dfrac{x}{r} = \dfrac{20}{50.3}=0.3976. \end{equation*}

Therefore, \(\theta_x = 66.6^{\circ}\text{.}\)

Solution 3. c

Similarly, the dot product between the given position and \(\hat j \) vector will give us the cosine of angle with the \(y \) axis.

\begin{equation*} \cos\, \theta_y = \dfrac{y}{r} = \dfrac{30}{50.3}=0.596. \end{equation*}

Therefore, \(\theta_y = 53.4^{\circ}\text{.}\)

Solution 4. d

Similarly, the dot product between the given position and \(\hat k \) vector will give us the cosine of angle with the \(z \) axis.

\begin{equation*} \cos\, \theta_z = \dfrac{z}{r} = \dfrac{35}{50.3}=0.6958. \end{equation*}

Therefore, \(\theta_z = 45.9^{\circ}\text{.}\)

Exercises 4.1.3 Exercises

1. Direction of Position Vector from a Direction Cosine Calculation.

A position vector makes \(120^{\circ}\) with respect to the positive \(x\) axis and \(90^{\circ}\) with respect to the positive \(y\) axis. What angle does it make with respect to the positive \(z\) axis?

Hint.

Use the identity \(\cos^2\, \theta_x + \cos^2\, \theta_y + \cos^2\, \theta_z = 1\)

Answer.

\(30^{\circ},\ 150^\circ.\)

Solution.

Using the identity \(\cos^2\, \theta_x + \cos^2\, \theta_y + \cos^2\, \theta_z = 1\text{,}\) we get

\begin{equation*} \cos\,\theta_z = \pm\sqrt{1- \dfrac{1}{4} - 0 } = \pm\dfrac{\sqrt{3}}{2} \end{equation*}

Therefore, \(\theta_z = 30^{\circ},\ 150^\circ\text{.}\) We need more information about the octant the vector points to choose between the two values.

Prev Top Next