Position on a Circle

Section 5.1 Position on a Circle

Subsection 5.1.1 Arc Length and Angle Subtended

When an object is moving in a circle, you can quantify its motion either by the distance covered on the circle or by the angle rotated about the center. The distance covered on the circle is called arc length and the angle at the center is called angle subtended.

The distance and angle must be cumulative since the position repeats and we are interested in movement during some duration of time. Therefore, we must add multiples of \(2\pi\) radians for each cycle in the counterclockwise direction and \(-2\pi\) radians for each cycle in the clockwise direction

There is a simple relation between arc length, denoted by \(s \text{,}\) corresponding angle \(\theta \) subtended at the center, and the radius \(R\) of the circle.

\begin{equation*} s = \theta\,R\ \ \ \ (\theta \text{ in radians.}) \end{equation*}

The relation between radians and degrees is

\begin{equation*} \pi\text{ radians} = 180^\circ. \end{equation*}

Thus, angle \(\theta\) covered when going once around is \(\theta=2\pi\) radians. This gives the distance \(D\) around the circle once to be

\begin{equation*} D = 2\pi R. \end{equation*}

This distance is called circumference of the circle.

In a circular motion, the direction of velocity changes continuously. Thus, in addition to the direction of vector quantities such as velocity and acceleration, we also describe the motion by a sense of rotation. For instance, when we look at the tip of a grandfather clock’s “minutes arm”, it goes around in circle. That sense of circular motion is called clockwise. You can also get this sense by folding left hand around the thumb with thum pointed up (Credit: https://commons.wikimedia.org/wiki/File-Clock-JungHans-6932.jpg). That is why clockwise sense is sometimes called left-handed.

The opposite sense is called counterclockwise>. You can get the counterclockwise sense by using your right hand and try to fold your fingers around the thumb, when the thumb is pointed up. This is the so-called right-handed sense.

Subsection 5.1.2 Position and Displacement on a Circle

Position vector \(\vec r\) of a particle P with respect to the center O of the circle has magnitude \(R\text{,}\) the radius of the circle, and direction radially from O to P. Let \(\theta\) be the counterclockwise angle of P with respect to positive \(x\) axis. Then, \(x\) and \(y\) components of \(\vec r\) will be

\begin{equation*} x = R\, \cos\, \theta,\ \ y = R\, \sin\, \theta. \end{equation*}

It is sometimes written using Cartesian unit vectors as

\begin{equation*} \vec r = x\, \hat i + y\, \hat j = (R\, \cos\, \theta)\,\hat i + (R\, \sin\, \theta)\, \hat j. \end{equation*}

Let \(\vec r_1\) be the position at \(t=t_1\) and \(\vec r_2\) be the position at \(t=t_2\text{.}\) Then, displacement \(\Delta \vec r\) during an interval \(\Delta t=t_2-t_1\) is

\begin{align*} \Delta \vec r \amp = \vec r_2 - \vec r_1,\\ \amp = (x_2 - x_1)\, \hat i + (y_2 - y_1)\, \hat j, \end{align*}

We can express this using radius of circle and angles.

\begin{align*} \Delta \vec r \amp = R(\cos \theta_2 - \cos \theta_1)\, \hat i + R(\sin \theta_2 - \sin \theta_1)\, \hat j,\\ \amp = 2 R \left( -\sin \dfrac{\theta_2 + \theta_1}{2} \, \hat i + \cos\dfrac{\theta_2 + \theta_1}{2} \, \hat j \right)\sin \dfrac{\theta_2 - \theta_1}{2}, \end{align*}

where I used trig identities for \(\cos A - \cos B\) and \(\sin A - \sin B\text{.}\)

\begin{align*} \amp \sin A - \sin B = 2 \cos\,\dfrac{A+B}{2}\, \sin\,\dfrac{A-B}{2},\\ \amp \cos A - \cos B = -2 \sin\,\dfrac{A+B}{2}\, \sin\,\dfrac{A-B}{2}, \end{align*}

Displacement for Small Intervals

The displacement formula for finite intervals simplifies considerably for small time intervals. Let

\begin{align*} \Delta \theta \amp = \theta_2 - \theta_1,\ \ \text{ and }\ \ \theta = \dfrac{\theta_2 + \theta_1}{2}. \end{align*}

For small \(\Delta\theta\text{,}\) we can approximate \(\sin(\Delta\theta/2)\) to be

\begin{equation*} \sin(\Delta\theta/2) \approx \Delta\theta/2, \end{equation*}

using \(\sin(x)\approx x\) for small \(x\text{.}\)

Therefore, displacement for small time intervals around angle \(\theta\) will be

\begin{equation*} \Delta \vec r = R\,\Delta\theta\,\left( -\hat i\, \sin \theta + \hat j\, \cos \theta \right). \end{equation*}

Vector \(\left( -\hat i\, \sin \theta + \hat j\, \cos \theta \right)\) is a unit vector in the direction of tangent to the circle as shown in Figure 5.6. We denote this unit vector by \(\hat u_\theta\text{.}\)

\begin{equation*} \Delta \vec r = R\,\Delta\theta\, \hat u_\theta. \end{equation*}

That is for small time intervals, displacement has magnitude \(R\,\Delta\theta\text{,}\) which is the arc length corresponding to the angle subtended, and direction is tangent to the circle. This makes sense since for small angles, the direct distance will be very close to the distance on the circle.

Example 5.7. Position, and Displacement on a Circle.

A child in a merry-go-round is moving in a circle of radius \(4\text{ m}\text{.}\) At some instant, let \(t = 0 \text{,}\) the child is at a point labeled A. Other positions of interest in our problem are B and C in Figure 5.8.

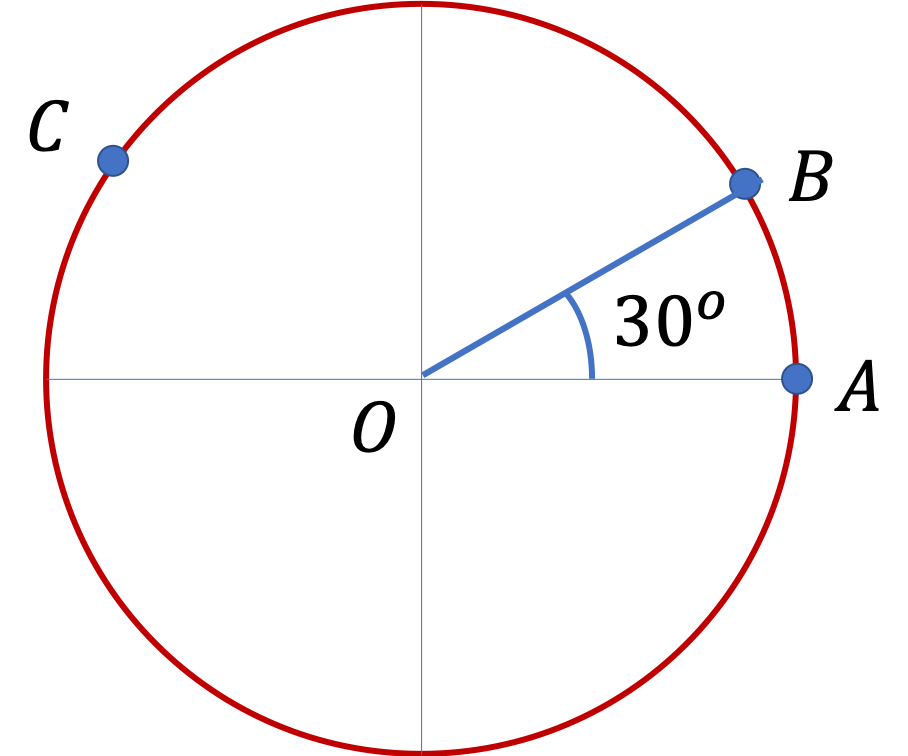
(a) At time \(t=2.0\text{ sec}\text{,}\) the child is at another point labeled B. How far distance on the arc between A and B has the child moved if the angle subtended at the center O between lines OA and OB is \(30^{\circ}\) (i) assuming the child has not gone full circle yet, (ii) assuming, the child has gone two full circles in addition to that shown in the figure?

(b) At some other instant, \(t = 3.0\text{ sec}\text{,}\) the child is at point C. If the distance moved between A and C on the arc is \(10.0\text{ m}\text{,}\) what is the angle subtended between OA and OC in degrees (i) assuming the child has not gone full circle yet, (ii) assuming, the child has gone two full circles in addition to that shown in the figure?

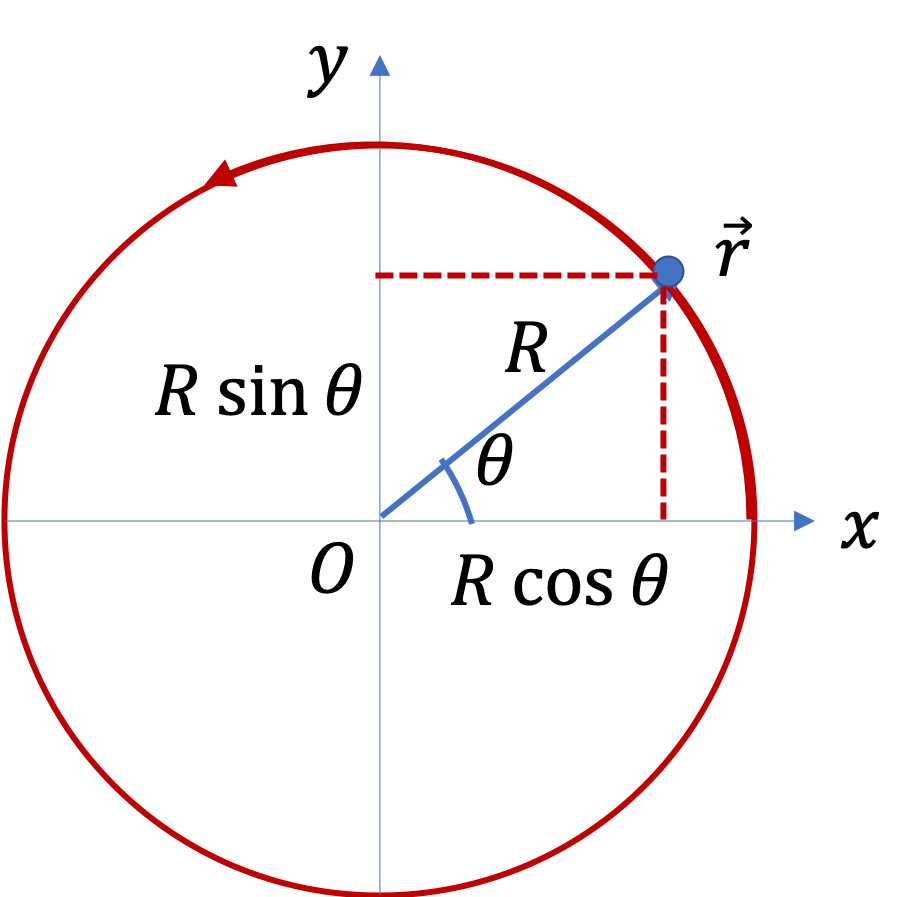
(c) Suppose you use a Cartesian coordinates with O at the center and OA towards the positive \(x \) axis, what are the coordinates of points A, B and C?

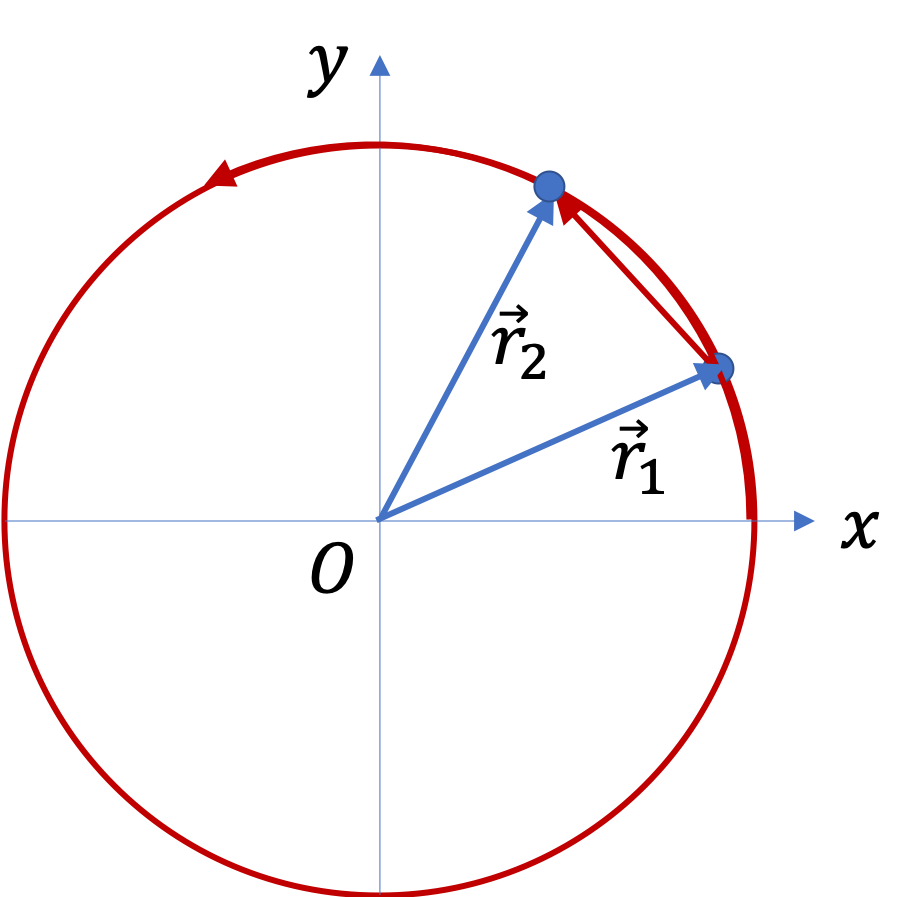
(d) What is the displacement between B and C?

Answer.

(a) (i) \(2.09\text{ m}\text{,}\) (ii) \(52.35\text{ m}\text{,}\) (b) (i) \(143.2^{\circ}\text{,}\) (ii) \(15.1\text{ rad}\text{,}\) (c) \((4.0\text{ m}, 0) \text{,}\) \(( 3.46\text{ m}, 2\text{ m})\text{,}\) \(( -3.20\text{ m}, 2.39\text{ m})\) (d) \(6.67\text{ m}\) at \(3.35^{\circ}\) clockwise from the negative \(x \) axis.

Solution 1. a

(i) The distance on the arc is related to the angle in radian, so we convert degrees to radians.

\begin{equation*} s = R\theta = 4.0\times \dfrac{30\times \pi}{180} = 2.09\text{ m}. \end{equation*}

(ii) Since the child has gone two full circles in addition to this, we have

\begin{equation*} s = 2.09\text{ m} + 2\times 2\pi R = 52.35\text{ m}. \end{equation*}

Solution 2. b

(i) The angle in radian will be

\begin{equation*} \theta = \dfrac{s}{R} = \dfrac{10.0}{4.0} = 2.5\text{ rad}. \end{equation*}

We need to convert this to degrees.

\begin{equation*} \theta = 2.5 \times 180 / \pi = 143.2^{\circ}. \end{equation*}

(ii) Now, we will need to add angles covered for two additional full circles.

\begin{equation*} 2.5\text{ rad} + 2\times 2\pi\text{ rad} = 15.1\text{ rad}. \end{equation*}

Solution 3. c

Using the axes given, we will get the following for the positions of A, B, and C.

\begin{align*} \amp \vec r_A = (4.0\text{ m}, 0),\\ \amp \vec r_B = (4.0\,\cos\,30^{\circ}, 4.0\,\sin\,30^{\circ}) = ( 3.46\text{ m}, 2\text{ m}),\\ \amp \vec r_C = (4.0\,\cos(2.5\text{ rad}), 4.0\,\sin(2.5\text{ rad})) = ( -3.20\text{ m}, 2.39\text{ m}), \end{align*}

Solution 4. d

Now, since we know the coordinates of B and C, it is trivial to get the \(x \) and \(y\) components of the displacement vector. From

\begin{equation*} \Delta \vec r = \vec r_C - \vec r_B, \end{equation*}

we get

\begin{align*} \amp \Delta x = x_C - x_B = -3.20-3.46 = -6.66\text{ m}, \\ \amp \Delta y = y_C - y_B = 2.39-2 = 0.39\text{ m}. \end{align*}

We can get the magnitude and direction of the displacement from these components.

\begin{align*} \amp\text{Magnitude: } \Delta r = 6.67\text{ m}, \\ \amp \theta = \tan^{-1}\dfrac{0.39}{-6.66} = -3.35^{\circ}. \end{align*}

Since \((-6.66,0.39)\) is in the second quadrant, the direction is \(3.35^{\circ}\) clockwise from the negative \(x \) axis.

Exercises 5.1.3 Exercises

1. Rolling a Cylinder by Pushing on the Axle (JEE, 2020).

A small roller of radius \(R\) with an axle of radius \(r\) is placed on a horizontal floor and a meter ruler is positioned horizontally on the axle with one edge of the ruler on top of the axle as shown in Figure 5.9.

The ruler is now pushed gently on the axle so that the ruler rides on the axle and the roller rolls without slipping on the floor. After the roller has moved a distance \(D\text{,}\) how far would the tip of the ruler move? (Adapted from Indian JEE, 2020)

Hint.

The axle rotates same amount of angle as the entire roller, but a point on axle moves different amount in space.

Answer.

\(\frac{D\,r}{R}\text{.}\)

Solution.

Note that the axle and roller rotate same amount of angle, but while roller rolls a distance \(2\pi R\) in one full rotation, a point on axle moves only \(2\pi r\text{.}\) Therefore, when roller has moved a distance \(D\text{,}\) the tip of the ruler will move

\begin{equation*} \frac{2\pi r}{2\pi R}\; D = \frac{D\,r}{R}. \end{equation*}

Prev Top Next