Quantum Model of Conduction in Metals

Section 53.4 Quantum Model of Conduction in Metals

While the classical model of metals gave reasonable explanations of some aspects of electrical and thermal conduction, it was deficient in some other aspects. We saw in the last chapter that an application of quantum mechanics to atoms gives us satisfactory explanation of many properties of atoms and molecules - spectroscopy, their arrangement in the periodic table, angular momentum, magnetic dipole moment, bonding between atoms, and so on. The questions now are: could an application of quantum mechanics to a block of solid also give us insights into properties of solids, and is it mathematically possible to solve the complicated problem of electrons in solids? Recall that solving Schr\"odinger equation for any atom beyond the Hydrogen atom is too difficult. If multielectron-atom problems are difficult, there is no hope of solving the problem of $10^22$ electrons in a metal sample. Clearly, we need drastic approximation such as the the one made in the Drude model. In this section we will look at the Drude model quantum mechanically.

Subsection 53.4.1 Fermi Level

Subsubsection 53.4.1.1 Free Electron Approximation

If electrons are considered free of each other, we can solve the problem of one electron first, and then use the Aufbau principle together with the Pauli’s exclusion principle to find the quantum state of the solid. Each electron in the metal would be considered to be confined to the body and surface of the metal. This is same as a particle in a box problem. To be concrete and for the sake of simplicity, suppose the metal is a cube of side $a$ with one corner at the origin. Then, the quantum wave function of any one electron will be

\begin{equation*} \psi_E(x,y,z) = \left(\frac{2}{a}\right)^{3/2}\sin\left( \frac{n_x\pi x}{a}\right) \sin\left( \frac{n_y\pi y}{a}\right) \sin\left( \frac{n_z\pi z}{a}\right), \end{equation*}

with quantum numbers $n_x = 1, 2, 3, \cdots\text{,}$ $n_y = 1, 2, 3, \cdots\text{,}$ $n_z = 1, 2, 3, \cdots\text{,}$ corresponding to energy

\begin{equation} E = \dfrac{\pi^2\hbar^2}{2 m a^2}\left( n_x^2 + n_y^2 + n_z^2\right). \tag{53.8} \end{equation}

According to Pauli’s exclusion principle, each state designated by the quantum numbers $(n_x, n_y, n_z)$ can have at most two electrons, one with up spin and the other with down spin. For instance, the first electron will go in the lowest energy state $(1,1,1)\text{,}$ the second electron can also go in this state but with opposite spin. The first two electrons each have energy

\begin{equation*} E = \dfrac{3\pi^2\hbar^2}{2 m a^2}. \end{equation*}

The third electron will have to go in the next higher energy state, which will be either $(2,1,1)$ or $(1,2,1)$ or $(1,1,2)\text{.}$ Suppose, we place the third electron in $(2,1,1)\text{,}$ then the fourth electron can have the same spin as the third electron if it is in $(1,2,1)$ or $(1,1,2)$ states. In this way, a total of six electrons will go into states $(2,1,1)\text{,}$ $(1,2,1)\text{,}$ and $(1,1,2)\text{,}$ which all have the same energy.

\begin{equation*} E = \dfrac{3\pi^2\hbar^2}{m a^2}. \end{equation*}

The next six electrons go into $(2,2,1)$ or $(1,2,2)$ or $(2,1,2)$ states which all have the same energy

\begin{equation*} E = \dfrac{9\pi^2\hbar^2}{2 m a^2}. \end{equation*}

This process of successively filling the allowed states will be continued till we have placed all conduction electrons in the available quantum states. The highest energy level occupied is called the Fermi level. We will next calculate the expression of the energy of the Fermi level.

Subsubsection 53.4.1.2 Fermi Energy

In a macroscopic size metal, say 1 cm $\times$ 1 cm $\times$ 1 cm, there will be a large number of conduction electrons, of the order of the Avogadro number. Suppose there are $N_e$ total conduction electrons. They will fill up $N_e/2$ states. We can calculate the energy of the highest energy state occupied by the following argument.

Note that the quantum numbers $(n_x, n_y, n_z)$ in the energy expression Eq. (53.8) come as sum of their squares. Therefore, if we think of $(n_x, n_y, n_z)$ as the $x$-, $y$- and $z$-coordinates of the $n$-space, energy will depend on the ``radial’’ distance in that space. Let us denote the ``radial’’ distance in this space by $n\text{.}$

\begin{equation} E = \dfrac{\pi^2\hbar^2}{2 m a^2}\: n^2.\tag{53.9} \end{equation}

The states to fill up go as $n=\sqrt{3}\text{,}$ $\sqrt{6}\text{,}$ $\sqrt{9}\text{,}$ $\sqrt{11}\text{,}$ $\sqrt{12}\text{,}$ and so on. Eventually, the spacing between the successive $n$ values narrow and we can treat $n$ as a continuous variable. If the final $n$ to fill up by conduction electrons is $n_F\text{,}$ then the volume of the sphere of ``radius’’ $n=n_F$ in the positive octant will be occupied with each $n$ being occupied by two electrons, one an up spin and the other the down spin. Therefore, this volume times 2 will equal the total number of conduction electrons, $N_e\text{.}$

\begin{equation*} \left(\frac{1}{8}\: \times \:\frac{4}{3} \pi n_F^3\right)\times 2 = N_e. \end{equation*}

This gives the following for $n_F\text{.}$

\begin{equation*} n_F = \left( \frac{3N_e}{\pi}\right)^{1/3} \end{equation*}

Now, putting $n=n_F$ in Eq. (53.9) gives us the energy of the highest occupied level, which we denote by $E_F\text{.}$

\begin{equation*} E_F = \dfrac{\pi^2\hbar^2}{2 m a^2}\: n_F^2 , \end{equation*}

which upon simplification yields

\begin{equation} E_F = \dfrac{ \hbar^2}{2 m }\: \left( \frac{3\pi^2 N_e}{a^3} \right)^{2/3}, \tag{53.10} \end{equation}

Often it is written by replacing $a^3$ by the volume $V$ of the cube.

\begin{equation} E_F = \dfrac{ \hbar^2}{2 m }\: \left( \frac{3\pi^2 N_e}{V} \right)^{2/3}. \tag{53.11} \end{equation}

The energy $E_F$ is called Fermi energy and the energy level with $E=E_F$ is called the Fermi level. The Fermi energy of a system is related to the energy required to extract an electron from the metal, which is the work function of the metal.

Subsubsection 53.4.1.3 Density of States

How many states will there be between energy $E$ and $E+\Delta E\text{?}$ The number of states below any energy level is one-eights (times two) of the volume of the sphere of radius $n$ corresponding to that energy. Thus, the number of states $\Delta \mathcal{N}$ in the energy range $E$ to $E+\Delta E$ will be

\begin{equation*} \Delta \mathcal{N} = 2\times \frac{1}{8}\left[\frac{4}{3} \pi (n+\Delta n)^3 - \frac{4}{3} \pi n^3\right]. \end{equation*}

Simplifying this we get

\begin{equation*} \Delta \mathcal{N} = \pi n^2 \Delta n, \end{equation*}

where I have dropped higher power of $\Delta n$ since we are interested in infinitesimal $\Delta n\text{.}$ We can write this expression in terms of energy $E$ by noting that

\begin{equation*} E = \dfrac{\pi^2\hbar^2}{2 m a^2}\: n^2 \ \ \Longrightarrow\ \ \Delta E = \dfrac{\pi^2\hbar^2}{m a^2}\: n \Delta n. \end{equation*}

Therefore, the number of states between energy $E$ and $E+\Delta E$ is

\begin{equation*} \Delta \mathcal{N} = \pi\sqrt{2} \left( \frac{m}{\pi^2\hbar^2}\right)^{3/2} V \sqrt{E} \Delta E. \end{equation*}

Therefore, the number of states per unit energy range per unit volume, called the density of states, $\rho(E)$ is

\begin{equation} \rho(E) = \frac{\Delta \mathcal{N} }{V \Delta E} = \pi\sqrt{2} \left( \frac{m}{\pi^2\hbar^2}\right)^{3/2} \sqrt{E}.\tag{53.12} \end{equation}

This says that as you go on filling electrons in various states, the number of available states per unit energy of the last filled state increases with energy. This has the effect of most conduction electrons to end up near the highest energy state filled by the electrons.

Subsubsection 53.4.1.4 Fermi-Dirac Distribution

So far in our studies we have ignored the role of temperature. Our discussion above has tacitly assumed that the metal sample is at the absolute zero, $0K\text{,}$ temperature. At temperature $T=0K\text{,}$ there is no thermal energy available to push an electron into higher energy states above the Fermi level. If the sample is in thermal contact with a thermal bath at a non-zero temperature, $T > 0K\text{,}$ electrons at the Fermi level will be excited leaving some lower energy states unoccupied and some higher energy states occupied. For a metal we can also define a Fermi temperature $T_F$ by equating the thermal energy for that temperature to the Fermi energy of the metal.

\begin{equation*} k_BT_F = E_F,\ \ \Longrightarrow\ \ T_F = E_F/ k_B. \end{equation*}

We will see below that thermal effects are significant even when the temperature of the metal is well below the Fermi temperature for the metal. The probability that a state of energy $E$ is occupied at temperature $T$ (Kelvin) is given by the Fermi-Dirac distribution function give by

\begin{equation*} f_{\textrm{FD}} = \frac{1}{e^{(E-E_F)/k_BT} + 1}. \end{equation*}

To see the impact of temperature on a sample it is instructive to plot $f_{\textrm{FD}}$ at different temperatures. Figure 53.17 shows the Fermi-Dirac distribution function for gold at $0K$ and at $\frac{1}{10}T_F = 6,420K\text{.}$ The $T_F$ of gold was calculated from the Fermi energy of 5.53 eV of gold as

\begin{equation*} T_F = \frac{E_F}{k_B} = \frac{5.5\ \textrm{eV}}{8.62\times 10^{−5}\:\textrm{eV/K}} = 64,200\:\textrm{K}. \end{equation*}

From the figure it is clear that, although the Fermi energy is $5.53\text{ eV}\text{,}$ the probabilities of the occupancy of states from around 2.5 eV and up are less than 1 at $T = 0.1 T_F\text{.}$ While all states below $E=E_F$ are occupied at $T=0K\text{,}$ some of the states below $E=E_F$ will be un-occupied at $T>0K\text{.}$ For instance, gold has $5.90 \times 10^{22}$ conduction electrons per $\text{cm}^3\text{.}$ At $T=0K$ all of these electrons will be in states with $E\le E_F\text{.}$ At $T>0K\text{,}$ some of these electrons will be promoted to states with $E>E_F$ and therefore, some of the states below the Fermi level will be empty.

Figure 53.17. The effect of temperature on the distribution of electrons in available quantum states. The top figure is the density of available states in the free-electron approximation. The middle figures are the Fermi-Dirac distribution at $T = 0K$ and $T = 6420K\text{,}$ which is one-tenth of the $T_F$ of gold. The bottom figure shows the product of the two and displays actual density of states occupied. The temperature mostly affects the distribution near the Fermi energy.

shows the density of the available states and the density of occupied states with respect to energy of the state at $T=0K$ and $T = 0.1 T_F$ for a gold sample. The number of states per unit energy per unit volume varies as $\sqrt{E}$ as given in Eq. (53.12) and the probability that any one of these states is occupied is given by the Fermi-Dirac distribution $f_{\textrm{FD}}\text{.}$ The density of occupied states will equal the density of states times the probability that the state is occupied given by $f_{\textrm{FD}}\text{.}$ That is

\begin{equation} \rho_{\textrm{occupied}} (E) = \rho(E) \times f_{\textrm{FD}}. \tag{53.13} \end{equation}

While the lowest energy electrons are not affected much by the thermal energy that is not too large, the electrons at the Fermi level are affected greatly. This can be seen in the expression of the Fermi-Dirac distribution. The dependence on energy is is exponential in the difference $E-E_F$ and temperature $T\text{.}$ The limits of $f_{\textrm{FD}}$ in $E>> E_F$ and $E \ll E_F$ limits are

\begin{equation*} f_{\textrm{FD}} = \frac{1}{e^{(E-E_F)/k_B T} + 1} = \left\{ \begin{array}{ll} 1 \amp \quad\quad E \ll E_F\\ 0 \amp \quad\quad E>> E_F \end{array} \right. \end{equation*}

Thus, the only electrons that play active role in the electrical properties of a metal are the ones whose energies are close to the Fermi energy.

Subsection 53.4.2 Mean Free Path of Electrons in Metal

To study conduction it is useful to introduce a speed associated with an electron at the Fermi level, called the Fermi speed $v_F\text{,}$ by equating the Fermi energy to the kinetic energy of the electron. Since the electron speed even the ones at the Fermi level are in the non-relativistic regime we use the nonrelativistic formula of the kinetic energy.

\begin{equation*} \frac{1}{2} m v_F^2 = E_F,\ \ \ v_F = \sqrt{2E_F/m}. \end{equation*}

For simplicity of discussion we will assume $T=0K\text{.}$ In this case, the speed of electrons in the metal will be between $0$ and $v_F$ which would correspond to the energy of the occupied states between $0$ and $E_F\text{.}$ In the absence of an applied electric field, the velocity of conduction electrons will be in all directions, or put another way, same number of electrons will flow in opposite directions. Therefore, even with large speed, there will be no net drift in any particular direction.

Due to the symmetry of directions in space, in the absence of an external applied field, the Fermi-Dirac distribution will be symmetric with respect to positive and negative components of the velocity in any direction. Now, if we apply an electric field pointed towards the negative $x$ direction, there will be an external force on the electron towards the positive $x$ direction, which will accelerate the electrons moving towards the positive $x$ direction and decelerate the electrons which were moving towards the negative $x$ direction. This will cause the shift of the Fermi-Dirac distribution with respect to the velocity towards the positive $x$ direction as shown in Figure 53.18.

Figure 53.18. The Fermi surface is centered at the origin in the velocity space when there is no external electric field. When an electric field is applied in the direction of negative $x$-axis, electrons pick up speed in the positive $x$-direction moving the Fermi surface to the right.

In Figure 53.18 we note that mostly the electrons at the Fermi level will be active in the conduction. They have the Fermi speed $v_F\text{.}$ Therefore, in place of the rms speed $v_{\textrm{rms}}$ used in the classical model we should use $v_F\text{.}$

\begin{equation*} \textrm{For quantum gas, use } v_F = \sqrt{2E_F/m}. \textrm{ in place of } v_{\textrm{rms}}. \end{equation*}

With this change we will notice a difference in the predicted conductivity with the conductivity now given by

\begin{equation} \sigma = \frac{ne^2\lambda}{m v_F}. \tag{53.14} \end{equation}

Recall that the problem with the Drude model was the short mean free path in the model. Now, since we are using electrons as waves, we would like to know what is the mean free path of the electron that would give the correct $\sigma\text{.}$ Solving Eq. (53.14) for $\lambda$ gives

\begin{equation} \lambda = \frac{m v_F\sigma}{ne^2}. \tag{53.15} \end{equation}

Checkpoint 53.19. Mean Free Path of an Electron in Metal.

Find the mean free path of an electron in gold using quantum gas formulas.

Hint.

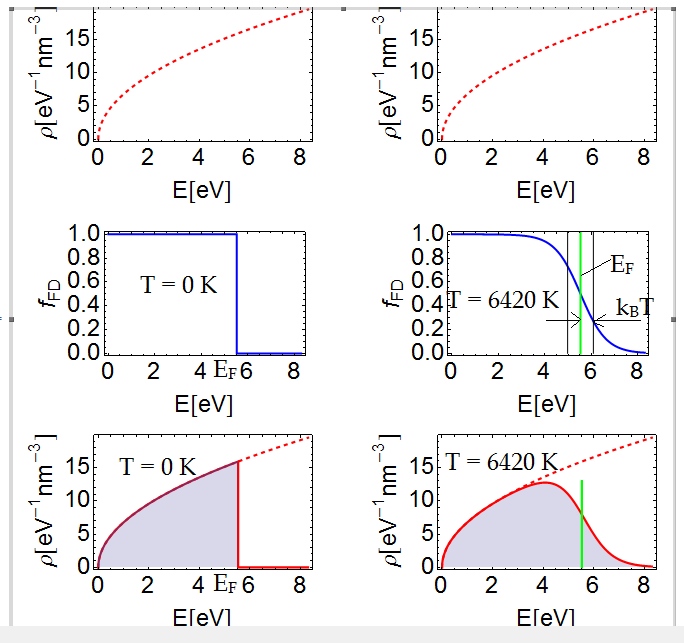
Get $v_F$ from Fermi energy.

Answer.

$34.6 \: \textrm{nm}\text{.}$

Solution.

Gold has Fermi energy $5.53 \text{ eV}\text{.}$ This gives the following for the Fermi speed $v_F\text{.}$

\begin{equation*} v_F = c\sqrt{2E_F/mc^2} = c\: \sqrt{\frac{2\times 5.53\: \textrm{eV} }{0.511\:\textrm{MeV}}} = 1.40\times 10^6\:\textrm{m/s}. \end{equation*}

Assuming that each gold atom contributes one electron to the conduction, we can readily calculate the density of conduction electrons from the density of gold $(19.32 \text{ g/cm}^3)$ and atomic weight $(197 \text{ g})$ with the result

\begin{equation*} n = 5.90 \times 10^{28}\:\textrm{electrons/m}^3. \end{equation*}

Putting numerical values in Eq. (53.15) we get the following for the mean free path.

\begin{align*} \lambda \amp = \frac{9.1\times 10^{-31}\:\textrm{kg} \times 1.40\times 10^6\:\textrm{m/s}\times 4.10\times 10^7\:\Omega^{-1}\textrm{m}^{-1}}{5.90 \times 10^{28}\:\textrm{electrons/m}^3 \times (1.6\times 10^{-19}\:\textrm{C})^2}\\ \amp = 3.46\times10^{-8}\:\textrm{m} = 34.6 \: \textrm{nm}. \end{align*}

Assuming the inter-atomic distance between gold atoms to be $0.30 \text{ nm}\text{,}$ the mean free path here is about 115 times longer than expected in the classical Drude model.

\begin{exercise} Assuming each atom of the (a) Ag, (b) Cu, and (c) Au contribute to the conduction, find the Fermi energy of these metals. Data: atomic weights: Ag 107.86, Cu 63.55, Au 196.97; mass density of metals, Ag 10.49 g/cm$^{3}$, Cu 8.96 g/cm$^{3}$, Au 19.30 g/cm$^{3}$. \end{exercise}

\begin{exercise} The electrical conductivity of copper at room temperature ( $27^{\circ}$C) is $ 5.96 \times 10^{7}\:\Omega^{-1}\textrm{m}^{-1}$. (a) Find the average time between collisions of electrons using quantum mechanical treatment. (b) What is the Fermi energy of copper. (c) What is the Fermi velocity of electrons of copper? (d) What is the mean free path of electrons at room temperature? Data: atomic weight Cu 63.55, mass density Cu 8.96 g/cm$^{3}$. \end{exercise}

Prev Top Next