The Heat Engine

Section 25.2 The Heat Engine

A device that does a conversion of heat to some other form of energy in a continuous process is called a heat engine. A heat engine must work in a cyclic process for the engine to convert heat to work continuously. Figure 25.1 shows the energy cycle of a heat engine schematically. As shown in this figure, an engine interacts with three external bodies.

The engine takes in energy $Q_H$ from a hot bath, such as a furnace.
The engine produces work $W$ through some mechanical apparatus, such as turbine which normally converts the mechanical energy to the electrical energy.
Finally, the engine gives up energy $Q_C$ to a cold bath, such as cold water, in order to return to the initial state and complete the cycle. That is, the cycle could not make use of all the energy in $Q_H$ in order for it to run in a cycle.

Figure 25.1. Schematics of energy flow in and out of a heat engine. The left panel shows the state of the working substance of the engine, shows as a fluid. In a cycle, the substance in state $a$ is heated by inputting heat $Q_H$ transforming to state $b\text{,}$ which expands the fluid leading to output of energy in the form of work $W\text{.}$ Finally, the substance is cooled by extracting heat $Q_C$ from the system, which brings the system back to the original state $a$ for the next cycle. The right panel shows the energetics of the cycle schemtically.

At the end of each cycle, the engine returns to the initial state, therefore, the net change in the internal energy of the engine must be zero.

\begin{equation*} \Delta U_\text{cycle a-b-c-a} = 0. \end{equation*}

In each cycle, engine takes up energy $Q_H$ and gives up energy $W+Q_C\text{.}$ Therefore, work by the engine would be the difference of heat in and heat out.

\begin{equation} W = Q_H - Q_C, \tag{25.1} \end{equation}

where all quantities are positive. The efficiency of a heat engine $\eta$ is defined as the ratio of the amount of net work $W$ the engine produces in one cycle to the amount of heat $Q_H$ transferred to the engine from the heat source.

\begin{equation} \eta = \frac{W}{Q_H}.\tag{25.2} \end{equation}

Putting the expression of $W$ from Eq. (25.1), the efficiency of a heat engine can he rewritten as follows.

\begin{equation} \eta = \frac{Q_H - Q_C}{Q_H} = 1- \frac{ Q_C}{Q_H}. \tag{25.3} \end{equation}

Clearly if all of heat taken $(Q_H)$ is converted into work, i.e. if $Q_C = 0\text{,}$ the efficiency will be $1\text{,}$ corresponding to a $100\%$-efficient engine. Experience has shown that this is not possible. We will study next an ideal engine called the Carnot engine that places an absolute limit on the highest possible efficiency of a heat engine.

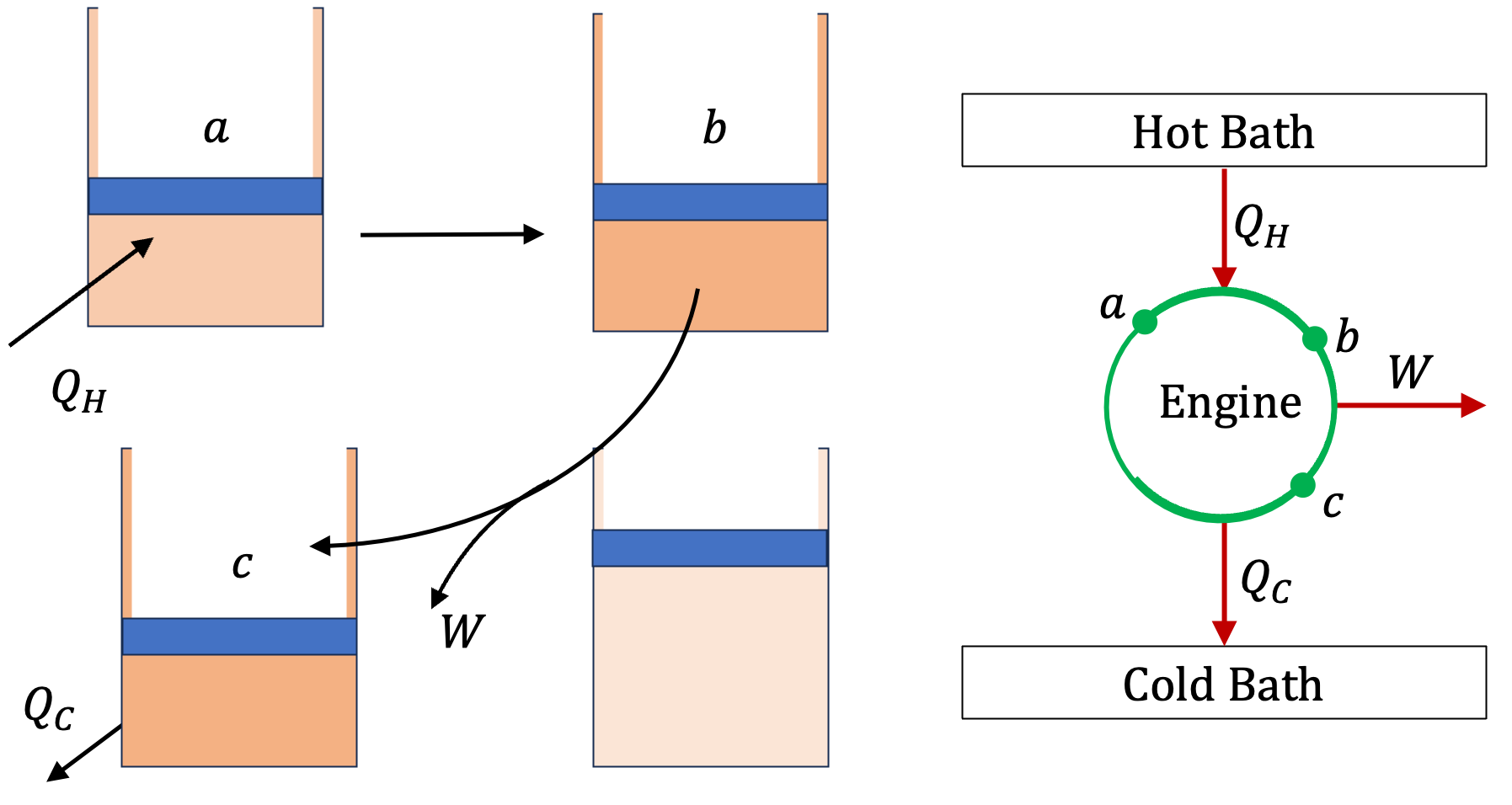
Example 25.2. Efficiency of a Steam Engine.

In a steam engine, a fixed amount of water is the working substance which goes through a full cycle, from liquid water at a certain temperature and pressure to steam, and then back to the liquid water at the original temperature and pressure.

The heat is put in the working substance, which is water here, in the step when liquid water is converted to steam. In some other parts of the cycle the steam expands and the energy comes out of steam when the steam pushes on the blades of a turbine, and in some other parts, the water has to be pumped and compressed, which requires work also.

In a certain steam engine, net work done by the working substance of the engine was $2000$ J per cycle. If the efficiency of the steam engine is $40\%\text{,}$ how much heat must be rejected in the cooling part of the cycle?

Answer.

$3000\text{ J}\text{.}$

Solution.

The net work $W$ by the engine and the efficiency $\eta$ of the engine are given here and we need to find $Q_C\text{.}$ From the efficiency $\eta$ and work $W\text{,}$ we can find $Q_H\text{,}$ and then using the energy balance, we will find $Q_C\text{.}$

\begin{equation*} \eta = \frac{W}{Q_H}\ \ \Longrightarrow\ \ Q_H = \frac{W}{\eta} = \frac{2000\ \text{J}}{0.4} = 5000\ \text{J}. \end{equation*}

Now, from the energy balance over one cycle, we know that in an engine, $W = Q_H-Q_C\text{.}$ Therefore,

\begin{equation*} Q_C = Q_H-W = 5000\ \text{J}- 2000\ \text{J} = 3000\ \text{J}. \end{equation*}

Exercises Exercises

1. Work Produced and Efficiecy of a Thermal Engine.

A heat engine operates between two temperatures such that the working substance of the engine absorbs $5000$ J of heat from the high temperature bath and rejects $3000$ J to the low temperature bath. The rest of the energy is converted into the mechanical energy of the turbine. (a) Find the amount of work produced by the engine. (b) Find the efficiency of the engine.

Hint.

(a) In a cycle W = Q. (b) Efficiency = Work/Heat in.

Answer.

(a) $2000$ J, (b) $40\%\text{.}$

Solution 1. a

First we note that in a cycle $\Delta U = 0\text{.}$ That means, in a cycle

\begin{equation*} W_\text{net,by} = Q_\text{net}. \end{equation*}

Taking engine as the system. That will make $Q_\text{in} \gt 0$ and $Q_\text{out} \lt 0\text{.}$ That will give

\begin{equation*} Q_\text{net} = 5000\text{ J} - 3000\text{ J} = 2000\text{ J}. \end{equation*}

Therefore,

\begin{equation*} W_\text{net,by} = 2000\text{ J}. \end{equation*}

Solution 2. b

The efficiency is the work by the engine divided by the heat into the engine at higher temperature.

\begin{equation*} \eta = \frac{W_{by}}{Q_{in}} = \dfrac{2000\text{ J}}{5000\text{ J}} = 0.4. \end{equation*}

As a percentage, it is 40%.

2. Efficiency of a Thermal Engine Producing Electricity.

A thermal engine produces $4$ MJ of electrical energy while operating between two thermal baths of different temperatures. The working substance of the engine rejects $5$ MJ of heat to the cold temperature bath. What is the efficiency of the engine?

Answer.

$44.4\%\text{.}$

Solution.

Given

\begin{equation*} W_{by} = 4\ \textrm{MJ}\ \ \textrm{and}\ \ Q_{out} = 5\ \textrm{MJ}. \end{equation*}

This gives

\begin{equation*} \ Q_{in} = W_{by} + Q_{out} = 9\ \textrm{MJ}. \end{equation*}

Therefore

\begin{equation*} \textrm{Efficiency} = \frac{W_{by}}{Q_{in}} = \frac{4\ \textrm{MJ}}{9\ \textrm{MJ}} = 0.444\ \ \textrm{or}\ \ 44.4\%. \end{equation*}

3. Efficiency of a Coal Power Plant.

A coal power plant consumes $100,000$ kg of coal per hour and produces $500$ MW of power. If the heat of combustion of coal is $30$ MJ/kg, what is the efficiency of the power plant?

Hint.

Use $Q=mh$ to get the energy produced by burning coal.

Answer.

60%

Solution.

From the mass $m$ and the heat of combustion $h$ of coal we get $Q_{in}\text{.}$ In one hour the heat entering the system at high temperature of the cycle is

\begin{align*} Q_{in}[\textrm{1 hour}] \amp = m h\\ \amp = 10^5\ \textrm{kg}\times 30\ \textrm{MJ/kg} = 3\times 10^6\ \textrm{MJ}. \end{align*}

The power produced is the work produced per unit time. The data is given in the unit $MW$, which is $MJ/s\text{.}$ In one hour the work produced will be

\begin{equation*} W_{by} = 500\ \textrm{MW} \times 3600\ \textrm{s} = 1.8\times 10^6\ \textrm{MJ}. \end{equation*}

Therefore,

\begin{align*} \textrm{Efficiency} \amp = \frac{W_{by}}{Q_{in}} \\ \amp = \frac{1.8\times 10^6\ \textrm{MJ}}{3\times 10^6\ \textrm{MJ}} = 0.6. \end{align*}

This is 60%.

Prev Top Next