Electric Potential and Electric Field

Section 31.7 Electric Potential and Electric Field

Subsection 31.7.1 (Calculus) Electric Potential From Electric Field

I have defined electric potential change based on work per unit charge required to move a charge from one location to another. This work is required due to need to balance the electric force on the charge by other charges. Denoting \(\phi_1\) for potential at point \(P_1\text{,}\) \(\phi_2\) for potential at point \(P_2\text{,}\) \(W_{1\rightarrow 2}\) the work required to move a test charge \(Q\) from \(P_1\) to \(P_2\) while balancing the electric force \(\vec F_e\text{,}\) the change is actually a work integral.

\begin{equation*} \phi_2 - \phi_1 = \frac{W_{1\rightarrow 2}}{Q} = -\frac{1}{Q}\int_1^2 \vec F_e\cdot d\vec r. \end{equation*}

Now, electric force can also be expressed as \(Q\) times the electric force of the other charges.

\begin{equation*} \vec F_e = Q\vec E. \end{equation*}

Therefore, we can write change in electric potential as

\begin{equation} \phi_2 - \phi_1 = - \int_1^2 \vec E\cdot d\vec r.\tag{31.19} \end{equation}

If point \(P_1\) is the reference point, we get the potential \(\phi\) at arbitrary point \(P\) by

\begin{equation} \phi = - \int_{\text{ref}}^{P}\, \vec E\cdot d\vec r.\tag{31.20} \end{equation}

The integral on the right side is independent of path. That means you can choose any path between the reference point and \(P\) to set up the integral for calculations. Only the end points of the integral matter. This conclusion is true only for electric field of static charges as we will see when we study dynamic fields. We say that electric force by static charges is a conservative force.

In case of spherical, cylindrical or planar, it is easier to obtain electric field by using Gauss’s law. In these cases, its often best to use Eq. (31.20) to obtain electric field as illustrated below in Exercise 31.7.5.3.

Subsection 31.7.2 (Calculus) Gradient of Potential and Curl of Electric Field

Taking gradient of both sides of Eq. (31.20) gives a local relation between electric field and electric potential at each point of space for static fields.

\begin{equation} \vec E = -\vec\nabla\, \phi.\ \ \ \ (\text{Static } \vec E)\tag{31.21} \end{equation}

This is often the way to get electric field from potential since working out or measuring potential is lot easier than electric field.

For instance, suppose we some how knew the electric potential of a charge \(q\) and we wanted to find electric field. So, it will go as follows.

\begin{equation} \vec E = -\vec \nabla \left[ \frac{1}{4\pi\epsilon_0}\ \frac{q}{r}\right],\tag{31.22} \end{equation}

where \(r\) is the spherical radial coordinate. Since we are dealing with spherical coordinates, we will use \(\vec \nabla\) in spherical coordinates, which is

\begin{equation*} \vec \nabla = \hat u_r \frac{\partial}{\partial r} + \hat u_\theta\frac{1}{r}\frac{\partial}{\partial \theta} + \hat u_\phi\frac{1}{r\sin\theta}\frac{\partial}{\partial \phi}. \end{equation*}

Using this in Eq. (31.22) gives the electric field expected for a point particle located at origin.

\begin{equation*} \vec E = \frac{1}{4\pi\epsilon_0}\ \frac{q}{r^2}\; \hat u_r. \end{equation*}

From Eq. (31.19) we see that change in electric potential will be zero if we move charge \(Q\) back to its original location. That is the line integral of the electric field over any closed loop will be zero.

\begin{equation} \oint_{1^1} \vec E\cdot d\vec r = 0.\ \ \ \ (\text{Static } \vec E)\tag{31.23} \end{equation}

By use of Stoke’s theorem of multivariat Calculus, you can also write this as curl of electric field equal to zero.

\begin{equation} \vec \nabla \times \vec E = 0.\tag{31.24} \end{equation}

Subsection 31.7.3 (Calculus) Laplace’s Equation

In the chapter on Gauss’s law, we found that divergence of electric field at any point is proportional to charge density at that point.

\begin{equation*} \vec\nabla\cdot\vec E = \dfrac{\rho}{\epsilon_0}. \end{equation*}

From the last section, we note that static electric field can be obtained from electric potential by gradient.

\begin{equation*} \vec E = -\vec\nabla \phi. \end{equation*}

Using this in the equation above, we find that

\begin{equation} \nabla^2 \phi = - \dfrac{\rho}{\epsilon_0}.\tag{31.25} \end{equation}

Here \(\nabla^2\) is called Laplacian. In Cartesian coordinates, it is just sum of the second derivatives.

\begin{equation*} \nabla^2 \phi = \dfrac{\partial^2 \phi}{\partial x^2} + \dfrac{\partial^2 \phi}{\partial y^2} + \dfrac{\partial^2 \phi}{\partial z^2}. \end{equation*}

Eq. (31.25) says that, laplacian of potential is zero at all points where charge density is zero.

\begin{equation} \nabla^2 \phi = 0,\ \ \text{where }\rho=0.\tag{31.26} \end{equation}

This equation is called Laplace’s equation. Much of more complicated statics problems are handled by solving Laplace’s equation.

Subsection 31.7.4 Electric Potential in Constant Electric Field Region

In a region of constant electric field \(\vec E\text{,}\) such as between two large charged plates or near single charged plate or very close to any charged surface, potential difference between two points \(P_1\) and \(P_2\) is simply

\begin{equation} \phi_2 - \phi_1 = - E\, d\, \cos\theta,\tag{31.27} \end{equation}

where \(d\) is the distance between \(P_1\) and \(P_2\) and \(\theta\) is the angle between the direction of \(P_1\) to \(P_2\) and the direction of electric field as shown in Figure 31.27.

Exercises 31.7.5 Exercises

1. Electric Potential Difference in the Region of Constant Electric Field.

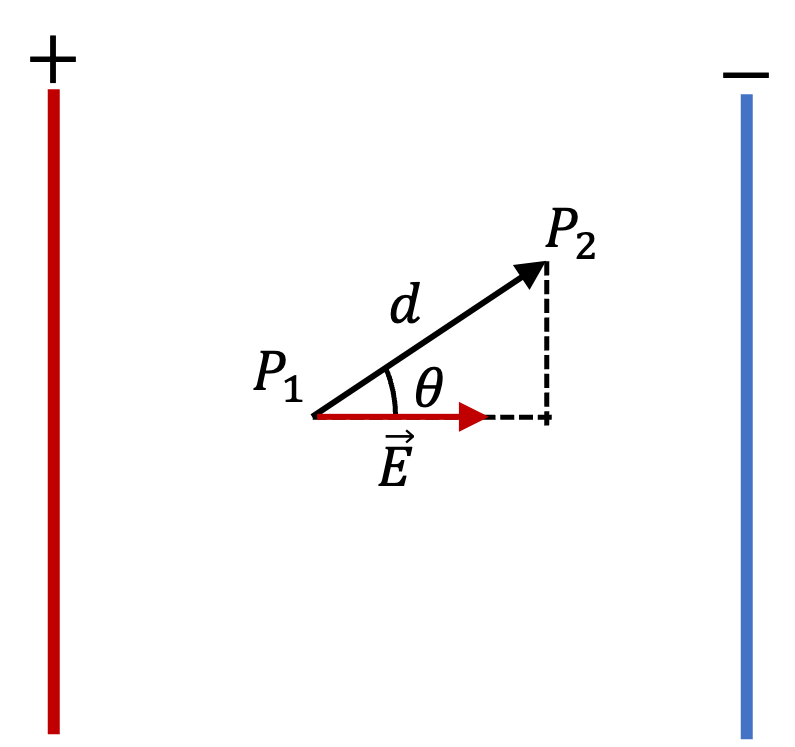
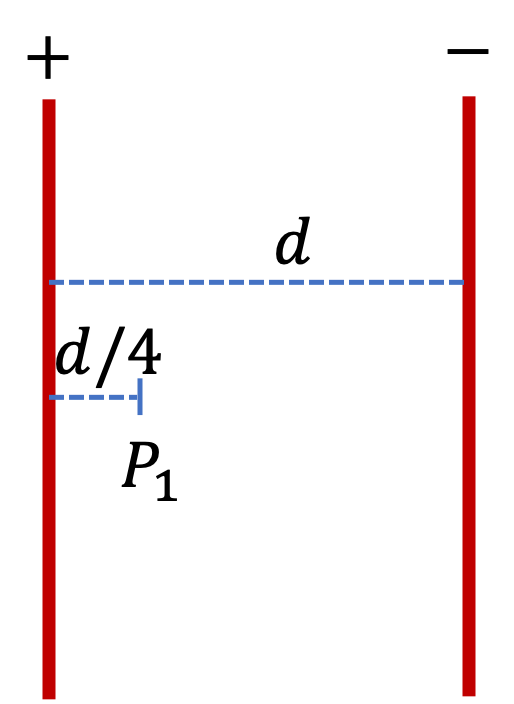
Two oppositely charged sheets with charge densities \(\pm\sigma\) face each other separated by a distance \(d\text{.}\) What is the potential difference between them?

Hint.

Make use the electric field between the plates.

Answer.

\(\frac{\sigma d}{\epsilon_0}\text{.}\)

Solution.

From applying Gauss’s law to one sheet we found that electric field by one sheet is \(\sigma/2\epsilon_0\text{.}\) The, by superposition, we get electric field between plates to be

\begin{equation*} \vec E = \frac{\sigma}{\epsilon_0}\hat u, \end{equation*}

where the unit vector \(\hat u\) is pointed from positive plate to negative plate. Now, we can make use of Eq. (31.19) to find the potential difference between plates. Integrating from negative plate to positive plate will mean \(d\vec r\) will be in the opposite direction to \(\hat u\text{,}\) which means the dot product will cancel the negative sign and result int

\begin{align*} \phi_{+} - \phi_{-} \amp = \int_{0}^{d} \frac{\sigma}{\epsilon_0} dr \\ \phi_{+} - \phi_{-} \amp = \frac{\sigma d}{\epsilon_0}. \end{align*}

2. Constant Electric Field between Parallel Plates from Electric Potential Difference.

Two large aluminum plates are connected to two terminals of a \(12\text{-volt}\) battery, which keeps all points of positive plate at electric potential \(\phi_+ = 12\text{ V}\) and all points of negative plate at electric potential \(\phi_- = 0\text{ V}\text{.}\) The separation between plates is \(4\text{ mm}\text{.}\)

(a) What is the electric field between the plates?

(b) What is the electric potential at point \(P_1\) located at a distance \(1.0\text{ mm}\) from the positive plate?

Hint.

(a) Use the fact that electric field between plates is constant. (b) Use electric field you found.

Answer.

(a) \(3000\text{ V}\text{,}\) (b) \(9\text{ V} \text{.}\)

Solution 1. (a)

Since electric field is constant between plates, the potential difference between plates will just be

\begin{equation*} \phi_+ - \phi_- = E d, \end{equation*}

where \(E\) is the magnitude of the electric field. Therefore,

\begin{equation*} E = \frac{\Delta\phi}{d}= \dfrac{12\text{ V}}{0.004\text{ m}} = 3000\text{ V/m}. \end{equation*}

Solution 2. (b)

Let \(x\) represent the distance of point \(P_1\) from the negative plate. Since electric field is constant, integration from negative plate to this point will give

\begin{equation*} \phi_{P_1} - \phi_{-} = E x. \end{equation*}

With \(\phi_{-}\) taken as zero reference, we get the potential at this point to be

\begin{equation*} \phi_{P_1} = E x = 3000\text{ V/m}\times 0.003\text{ m} = 9\text{ V}. \end{equation*}

3. (Calculus) Electric Potential Outside and Inside of a Charged Spherical Shell.

A copper sphere of radius \(R\) is charged with a total charge \(Q\text{.}\) The charge spreads out on the surface of the sphere with no charges inside the volume of the sphere. Use \(r=\infty\) as zero reference for electric potential.

(a) Find electric potential at a point outside the sphere.

(b) Find electric potential at a point inside the sphere. (Hint: it is not zero!)

Hint.

Use Gauss’s law to get E-field first. Then integrate E-field from reference point to the field point.

Answer.

(a) \(\dfrac{1}{4\pi\epsilon_0} \dfrac{Q}{r_\text{out}}\text{,}\) (b) \(\dfrac{1}{4\pi\epsilon_0} \dfrac{Q}{R}\text{.}\)

Solution 1. (a)

By applying Gauss’s law you should convince yourself that the magnitude of electric field of a charges shell depends on the distance \(r\) from the center of the shell with direction being radial from the center of the sphere.

\begin{equation*} E(r) = \begin{cases} 0 \amp r \lt R\\ \dfrac{1}{4\pi\epsilon_0}\, \dfrac{Q}{r^2} \amp r\gt R. \end{cases} \end{equation*}

For directions, we will assume \(Q\) to be positive for our calculations.

For electric potential at \(P_\text{out}\text{,}\) we will perform the integral in Eq. (31.20) from \(r=\infty\) to \(r=r_\text{out}\text{.}\) Since vector \(d\vec r = \hat u_r\, dr\) and \(\vec E\) is in \(\hat u_r\) direction, their dot product gives

\begin{equation*} \vec E \cdot d\vec r = E\, dr. \end{equation*}

Therefore, we get the following for the potential

\begin{align*} \phi_\text{out} \amp = -\int_{\infty}^{r_\text{out} }\, E(r)\, dr\\ \amp = -\dfrac{Q}{4\pi\epsilon_0} \int_{\infty}^{r_\text{out} }\, \dfrac{1}{r^2} \, dr\\ \amp = \dfrac{1}{4\pi\epsilon_0} \dfrac{Q}{r_\text{out}} \end{align*}

Solution 2. (b)

In the present case, we will need to perform integral from \(r=\infty\) to \(r=r_\text{in}\text{.}\) From (a), we already know what to expect fror any point from \(r=\infty\) to \(r=R\text{,}\) the radius. Present integral will then be divided up in two parts: \(r=\infty\) to \(r=R\) and \(r=R\) to \(r=r_\text{in}\text{,}\) the later will be zero since \(E\) in this domain is zero.

\begin{align*} \phi_\text{in} \amp = -\int_{\infty}^{r_\in}\, E(r) dr\\ \amp = \dfrac{Q}{4\pi\epsilon_0} \int_{\infty}^{R}\, \dfrac{1}{r^2} \, dr + 0 \\ \amp = \dfrac{1}{4\pi\epsilon_0} \dfrac{Q}{R}. \end{align*}

This says that electric potential is same throughout the interior of the metal sphere.

4. (Calculus) Potential of Uniformly Charged Sphere.

A spherical cloud of radius \(R\) has uniform charge density \(\rho\) (units: \(\text{C/m}^3\)). Find potential (a) at a point outside and (b) at a point inside the sphere. Use \(r=\infty\) as reference for the potential.

Hint.

Use Gauss’s law result for electric field.

Answer.

(a) \(\frac{1}{4\pi\epsilon_0}\,\frac{q}{r_\text{out}}\text{,}\) (b) \(\frac{1}{4\pi\epsilon_0} \frac{q}{R} \left( \frac{3}{2} - \frac{1}{2}\; \frac{r_{\text{in}}^2}{R^2} \right)\text{.}\)

Solution 1. (a)

Common to (a) and (b): Applying spherical symmetry case of Gauss’s law to the charge distribution, you can show that the electric field first. Let \(q\) be tht total charge in the sphere.

\begin{equation*} q = \frac{4}{3}\pi R^3 \rho. \end{equation*}

Using \(q\) and radial unit vector \(\hat u_r\text{,}\) electric field can be written as follows.

\begin{equation} \vec E = \begin{cases} \frac{1}{4\pi\epsilon_0} \frac{q}{r^2}\;\hat u_r \amp r \gt R\\ \frac{1}{4\pi\epsilon_0} \frac{q}{R^3}\; r\;\hat u_r \amp r \lt R \end{cases}\tag{31.28} \end{equation}

Now, we can integrate from reference at infinity to \(r=r_\text{out}\text{,}\) a point outside the sphere along a radial line. To set up the integral, we note that \(d\vec r = \hat u_r\, dr\) here for the radial path, giving us \(\vec E \cdot d\vec r = E\, dr\text{.}\) Hence, the potential is

\begin{align*} \phi_\text{out} \amp = -\frac{q}{4\pi\epsilon_0} \int_\infty^{r_\text{out}}\frac{1}{r^2}\; dr\\ \amp = \frac{1}{4\pi\epsilon_0}\,\frac{q}{r_\text{out}}. \end{align*}

That is, from outside, the spherical charge distribution acts like as it the entire charge is located at the center.

Solution 2. (b)

(b) Here, we split the integral into two parts since we need to integrate from infinity to a point inside and, according to Eq. (31.28), electric field has different expression outside and inside.

\begin{align*} \phi_\text{in} \amp = -\frac{q}{4\pi\epsilon_0} \int_\infty^{r_\text{in}}\frac{1}{r^2}\; dr\\ \amp = -\frac{q}{4\pi\epsilon_0} \int_\infty^{R}\frac{1}{r^2}\; dr -\frac{q}{4\pi\epsilon_0}\, \frac{1}{R^3}\, \int_R^{r_\text{in}}\;r\; dr\\ \amp = \frac{1}{4\pi\epsilon_0} \frac{q}{R} + \frac{1}{4\pi\epsilon_0} \frac{q}{2R} \left( 1 - \frac{r_{\text{in}}^2}{R^2} \right) \\ \amp = \frac{1}{4\pi\epsilon_0} \frac{q}{R} \left( \frac{3}{2} - \frac{1}{2}\; \frac{r_{\text{in}}^2}{R^2} \right). \end{align*}

5. (Calculus) Electric Potential of an Infintely Long Wire.

An infinitely long straight wire has a uniform charge density of \(\lambda=2.0\times 10^{-6}\text{ C/m}\text{.}\) What is the electric potential at a distance \(s=25\text{ cm}\) from the wire? State your reference point.

Hint.

Use electric field of a charged wire to deduce the formula for electric potential.

Answer.

\(5.0\times 10^4\text{ V}\) with zero potential reference at \(s=1\text{ m}\text{.}\)

Solution.

By applying Gauss’s law for cylindrical symmetry, we can show that magnitude of electric field at a distance \(s\) from the wire is given by the following formula.

\begin{equation*} E = \frac{\lambda}{2\pi\epsilon_0}\; \frac{1}{s}. \end{equation*}

Here, the field is in the cylindrical radial direction, as given by the unit vector \(\hat u_s\text{,}\) and the element \(d\vec r\) is also in the \(\hat u_s\) direction. Therefore, we will get their dot product to be

\begin{equation*} \vec E\cdot d\vec r = E\, ds. \end{equation*}

Now, let us integrate this along cylindrical radial line from \(s=s_0\text{,}\) the reference, to the point \(s=s\text{.}\) This will give us the following potential difference with respect to the reference point.

\begin{align*} \phi - \phi_\text{ref} \amp = - \frac{\lambda}{2\pi\epsilon_0}\; \int_{s_0}^s\frac{1}{s} ds \ \ \ (s_0\gt s)\\ \amp = - \frac{\lambda}{2\pi\epsilon_0}\; \ln\frac{s}{s_0}. \end{align*}

Choosing \(\phi_\text{ref} = 0 \text{,}\) we get

\begin{equation*} \phi = - \frac{\lambda}{2\pi\epsilon_0}\; \ln\frac{s}{s_0}. \end{equation*}

Note that we cannot choose reference distance, \(s_0=\infty\text{,}\) since that would give use zero potential at all points. Typically, we will choose \(s_0=1\) in the unit we express distance \(s\text{.}\) Thus, if we express \(s\) in meters, we will set \(s_0=1\text{ m}\) and write potential at \(s\) as

\begin{equation*} \phi = - \frac{\lambda}{2\pi\epsilon_0}\; \ln\,(s\text{ in m}). \end{equation*}

Numerically, now, with \(s=25\text{ cm}= 0.25\text{ m}\) we get

\begin{align*} \phi \amp = - \frac{2.0\times 10^{-6}}{2\pi\times 8.85\times 10^{-12}}\; \ln\,(0.25) = 5.0\times 10^4\text{ V}. \end{align*}

The potential is positive since our reference point at \(1\text{ m}\) is further away from positive charges than the field point at \(25\text{ cm}\text{.}\)

6. Electric Field Between Conductors of a Coaxial Cable.

A long coaxial cable has inner conductor maintained at potential \(V_0\) compared to the outer conductor. The inner conductor has radius \(a\) and the outer conductor has inner radius \(b\text{.}\) What is the electric field between the two conductors?

Hint.

Find \(\lambda\) on the inner conductor in terms of \(V_0\) by using the relation between electric field and potential expected for a cylindrical symmetry..

Answer.

\(\frac{V_0}{\ln\,(b/a) }\, \frac{1}{s}\, \hat u_s\text{.}\)

Solution.

The situation presented has cylindrical symmetry. Therefore, electric field will have only cylindrical radial dependence. Let \(\lambda\) denote linear charge density on the inner conductor. Then, by Gauss’s law we will have

\begin{equation*} \vec E = \frac{\lambda}{2\pi\epsilon_0}\, \frac{1}{s}\, \hat u_s. \end{equation*}

We need to find \(\lambda\) from \(V_0\text{.}\) For that, we look at the potential difference we expect by integrating from negative plate, chosen as reference for potential, to the positive plate we will get

\begin{equation*} V_0 = -\frac{\lambda}{2\pi\epsilon_0} \ln\,\frac{a}{b} = + \frac{\lambda}{2\pi\epsilon_0} \ln\,\frac{b}{a} \end{equation*}

This gives

\begin{equation*} \lambda = \frac{2\pi\epsilon_0 V_0 }{\ln\,(b/a) }. \end{equation*}

We use this in the electric field.

\begin{equation*} \vec E = \frac{V_0}{\ln\,(b/a) }\, \frac{1}{s}\, \hat u_s. \end{equation*}

7. (Calculus) Electric Field of a Spherical Charge Distribution from Electric Potential.

A spherical cloud of radius \(R\) has uniform charge density \(\rho\) (units: \(\text{C/m}^3\)). Find electric field (a) at a point outside and (b) at a point inside the sphere from the following known expressions for electric potential at these points where \(r_\text{in/out}\) are the radial spherical coordinates.

(a) \(\frac{1}{4\pi\epsilon_0}\,\frac{q}{r_\text{out}}\text{,}\) (b) \(\frac{1}{4\pi\epsilon_0} \frac{q}{R} \left( \frac{3}{2} - \frac{1}{2}\; \frac{r_{\text{in}}^2}{R^2} \right)\text{.}\) See Exercise 31.7.5.4.

Hint.

Use gradient of potential in spherical coordinates.

Answer.

(a) \(\frac{1}{4\pi\epsilon_0}\,\frac{q}{r_\text{out}^2}\; \hat u_r\text{,}\) (b) \(\frac{1}{4\pi\epsilon_0}\,\frac{q\, r_\text{in}}{R^3}\; \hat u_r\text{.}\)

Solution. (a) and (b)

Since the potentials are in spherical coordinates, it is best to work in spherical coordinates where \(\vec\nabla\) is

This has derivatives with respect to \(\theta\) and \(\phi\text{.}\) Since we will work with spherical coordinates in this problem, it is better to use symbol \(V\) for potential to avoid confusion.

\begin{align*} \vec E \amp = - \vec\nabla V\\ \amp = - \hat u_r \frac{\partial V}{\partial r} \end{align*}

For (a), we use

\begin{equation*} V(r) = \frac{1}{4\pi\epsilon_0}\,\frac{q}{r}, \end{equation*}

for (b), we use

\begin{equation*} V(r) = \frac{1}{4\pi\epsilon_0} \frac{q}{R} \left( \frac{3}{2} - \frac{1}{2}\; \frac{r^2}{R^2} \right). \end{equation*}

Carrying out the derivatives, we get the answers for (a) and (b) to be

\begin{equation*} \vec E = \begin{cases} \frac{1}{4\pi\epsilon_0}\,\frac{q}{r^2}\; \hat u_r \amp r \gt R\\ \frac{1}{4\pi\epsilon_0}\,\frac{q\, r}{R^3}\; \hat u_r \amp r \lt R. \end{cases} \end{equation*}

Prev Top Next