Angular Momentum

Section 9.6 Angular Momentum

Angular momentum is a fundamental property of a rotating body. In this section we will develop the concept systematically.

Subsection 9.6.1 Angular Momentum of a Particle

Let $\vec r $ be the position of a particle of mass $m $ and velocity $\vec v\text{.}$ The momentum of the particle is $\vec p = m\vec v$ and the angular momentum, to be denoted by $\vec l \text{,}$ is defined by the cross product of $\vec r $ and momnetum $\vec p \text{.}$

\begin{equation} \vec l = \vec r \times \vec p.\tag{9.18} \end{equation}

From this definition, magnitude of angular momentum will be

\begin{equation} l = r\,p\,\sin\,\phi,\tag{9.19} \end{equation}

where $\phi$ is the angle between vectors $\vec r $ and $\vec p\text{.}$

The direction of angular momentum is obtained by applying the right hand rule of cross product on vectors $\vec r $ and $\vec p\text{.}$ First, note that vector $\vec l$ will be perpendicular to the plane formed by vectors $\vec r$ and $\vec p\text{.}$ To use right hand rule, place $\vec r$ along the thumb of your right hand and $\vec p$ along any of the other fingers. Then, $\vec l$ will be coming out of the palm.

Example 9.37. Angular Momentum of a Particle Given its Trajectory and Mass.

Let the position vector of a particle of mass 50 g be the vector $(x=2, y=t^2, z=0)\text{,}$ where $t$ is in sec and coordinates in m. What is the angular momentum at $t = 30$ sec?

Answer.

$6\, \text{kg.m}^2/\text{s}\text{,}$ along $z$-axis.

Solution.

We find the expression for the velocity by taking the derivative of the position: $\vec v = (0,2 t, 0)\, \text{m/s}\text{.}$ From the definition $\vec L = \vec r \times \vec p$ we get

\begin{align*} L \amp = (2\hat u_x + t^2 \hat u_y) \times 0.05(2t\hat u_y)\\ \amp = 0.2t \hat u_z. \end{align*}

Subsection 9.6.2 Angular Momentum of a Particle in a Circular Motion

Consider a particle of mass $m$ moving in a circle of radius $R$ as shown in Figure 9.38. For a particle moving in a circle, the velocity is in the direction of the tangent to the circle.

Since the tangent of a circle is perpendicular to the radial line from the center, the angle between vectors $\vec r $ and $\vec p$ is $90^{\circ}\text{.}$

\begin{equation*} \phi = 90^{\circ}. \end{equation*}

This gives the magnitude of angular momentum to be

\begin{equation} l = m v R.\tag{9.20} \end{equation}

And, the direction of $\vec l$ is towards positive $z$-axis.

Subsection 9.6.3 A Particle in Circular Motion as Rotation

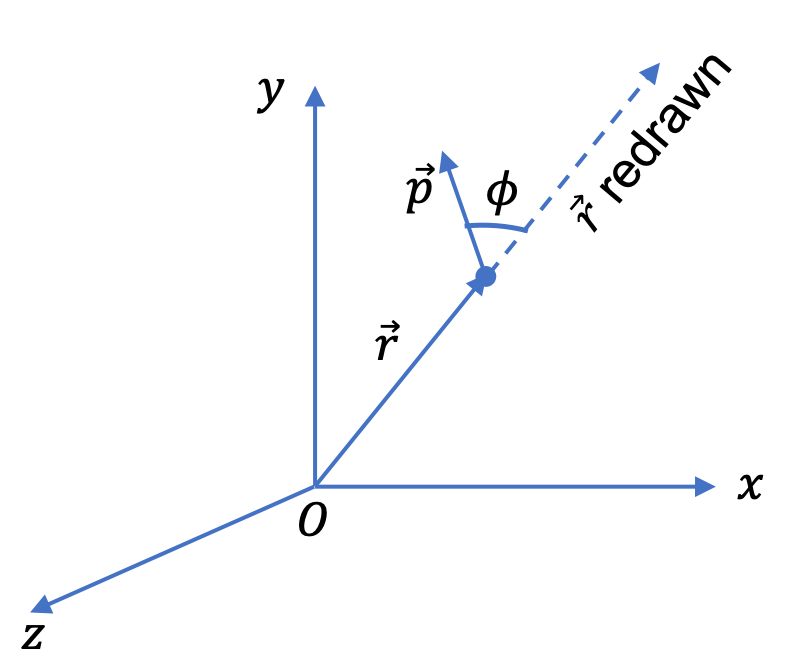
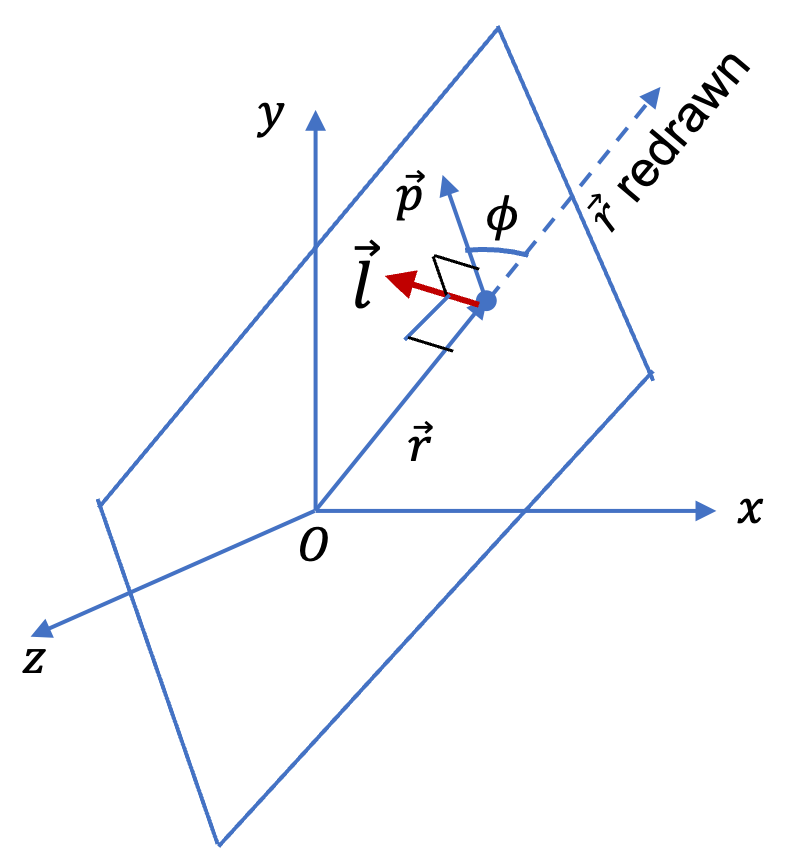
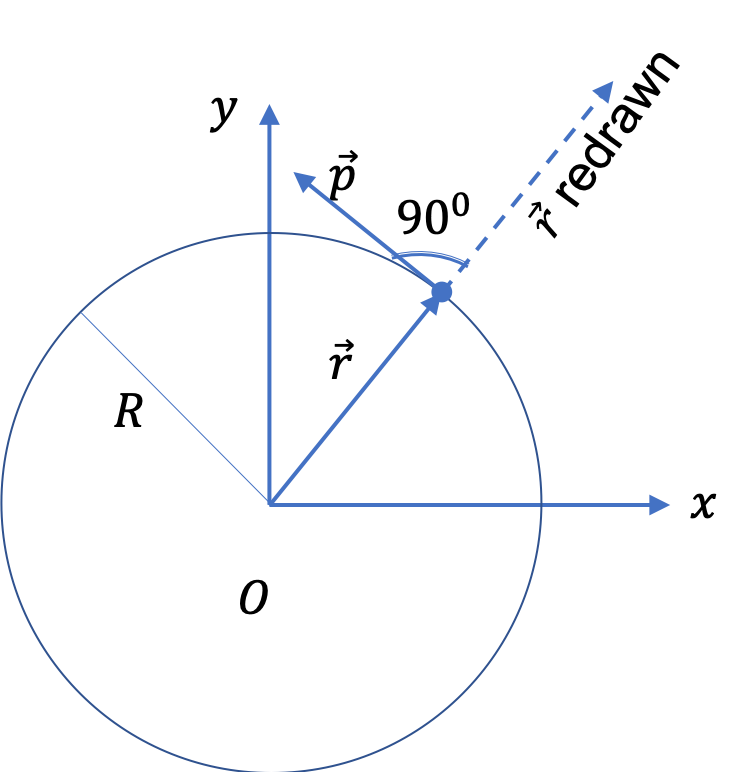
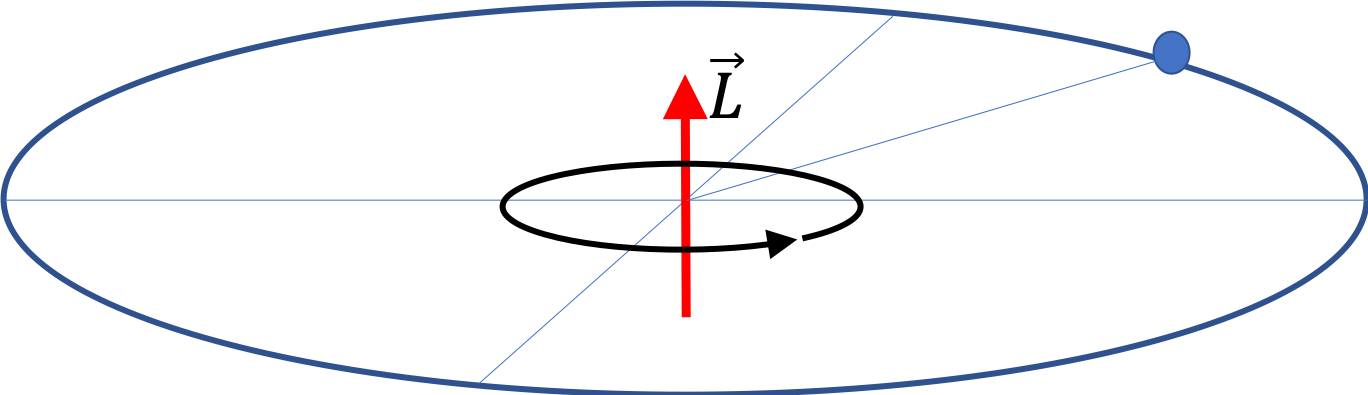
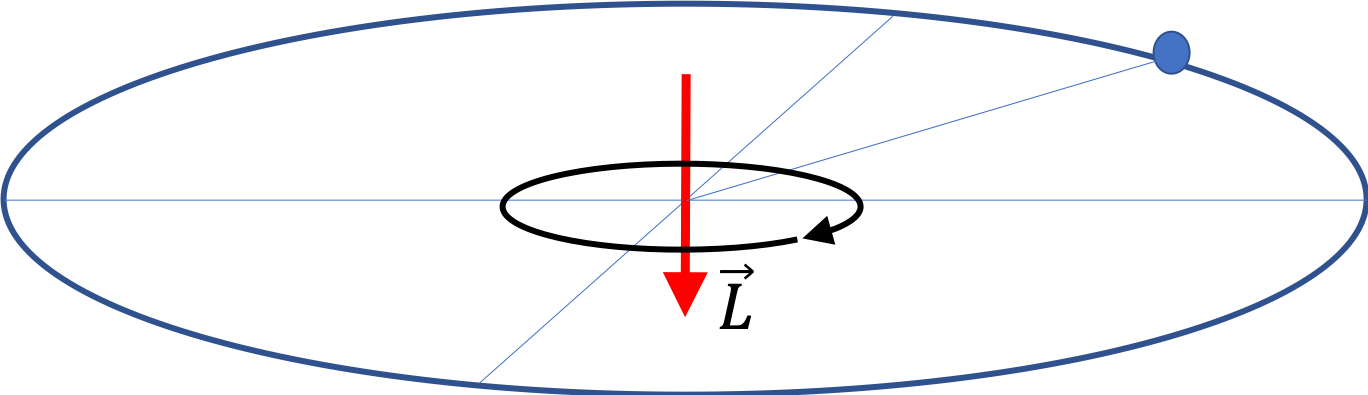
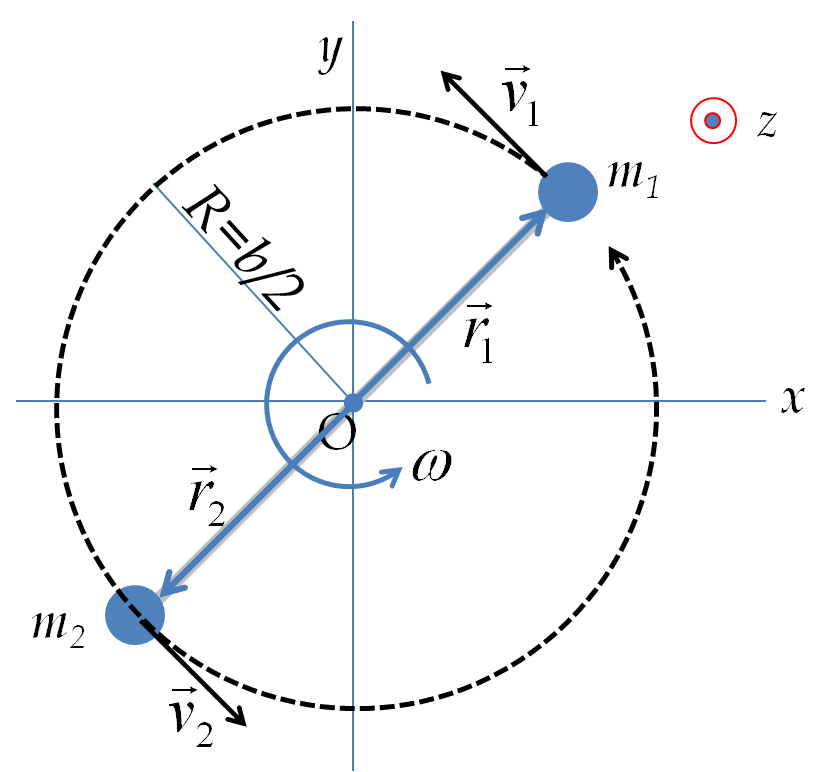
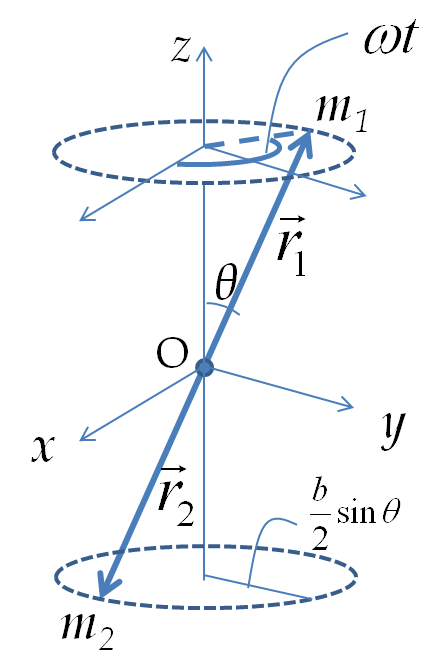
We can also think of the circular motion in Figure 9.38 as rotation about $z$-axis by quantifying the rotation by angle $\theta$ subtended by the radial line to the particle with positive $x$-axis. The distance $s$ covered on the arc of the circle will be related with angle covered $\theta$ by arc-angle relation.

\begin{equation*} s = R \theta. \end{equation*}

The rate of change in arc distance $s $ is the speed $v $ and rate of change of $\theta$ is the angular speed $\omega\text{.}$ Therefore,

\begin{equation*} v = R \omega. \end{equation*}

Substituting in Eq. (9.20) we get another useful expression for angular momentum.

\begin{equation} l = m R^2 \omega.\tag{9.21} \end{equation}

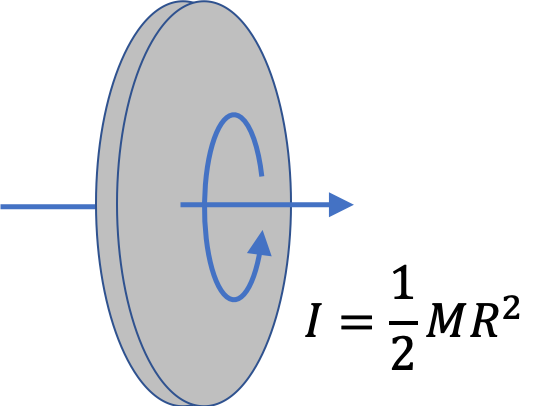
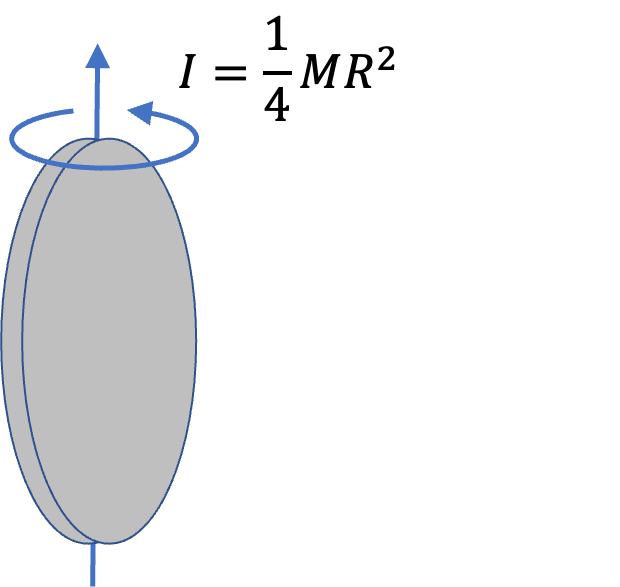
The quantity $m R^2$ in this formula is called moment of inertia of the particle about the axis. It is denoted by letter $I \text{.}$

\begin{equation} I\, (\text{of a particle at a distance }R \text{ from axis}) = m R^2.\tag{9.22} \end{equation}

In terms of moment of inertia and the angular velocity, the formula for the magnitude of the angular momentum for a particle moving in a circle takes a really simple form

\begin{equation} l = I\,\omega.\tag{9.23} \end{equation}

If you want to be more complete in your description, you could include information about the axis of rotation. For $z$-axis, this equation would be $l_z = I_{zz}\,\omega_z\text{.}$ The two subscripts for moment of inertia will become clear when we discuss moments of inertia of more complicated systems.

Example 9.39. Magnitude and Direction of Angular Momentum of a Ball Moving in a Circle.

A ball of mass $200\text{ grams}$ is moving in a circle of radius $25\text{ cm}$ with a uniform speed of $10\text{ m/s}\text{.}$ When observed from above the motion appears counterclockwise. Find the angular momentum about the center of the circle treating the ball as a point particle. Give both the magnitude and the direction of the angular momentum.

Answer.

$0.5\text{ kg.m}^2\text{/s}\text{,}$ up.

Solution.

The magnitude is

\begin{align*} L \amp = m v R\\ \amp = 0.2\text{ kg}\times 10\text{ m/s} \times 0.25\text{ m} \\ \amp = 0.5\text{ kg.m}^2\text{/s}. \end{align*}

Using the right hand rule, we find that the direction of angular monentum vector is pointed up. The direction is shown in the figure.

Example 9.41. Speed of a Ball Moving in a Circle with Angular Momentum Given.

The magnitude of the angular momentum of a steel ball of mass $400\text{ grams}$ moving in a circle in a horizontal plane of radius $50\text{ cm}$ is $3\text{ kg. m}^2\text{/s}$ about the center and the direction of the angular momentum vector is towards the ground.

Find the speed of the ball and the clockwise or counterclockwise sense of its motion in the circle as observed from above the circle. Treat the ball as a point particle.

Answer.

$15\text{ m/s}\text{,}$ clockwise.

Solution.

Let $v $ be the speed of the ball. From the definition, we get $m v R = L\text{,}$ which gives

\begin{equation*} v = \dfrac{L}{m R } = \dfrac{3\text{ kg. m}^2\text{/s}}{ 0.4\text{ kg} \times 0.5\text{ m} } = 15\text{ m/s}. \end{equation*}

By the right-hand rule, we get the direction of the motion is clockwise since the direction of the angular momentum is down.

Subsection 9.6.4 Angular Momentum of a Collection of Particles

Since, angular momentum is a vector, to get the momentum of the collection, we just need to work out the momenta of each particle and then add them up vectorially. Say, we have $N $ particles in the collection, with positions $\vec r_1\text{,}$ $\vec r_2\text{,}$ $\cdots\text{,}$ and similarlry for their momenta $\vec p_1\text{,}$ $\vec p_2\text{,}$ $\cdots\text{.}$ Then, their individual momenta will be

\begin{align*} \amp \vec l_1 = \vec r_1 \times \vec p_1,\\ \amp \vec l_2 = \vec r_2 \times \vec p_2,\\ \amp \cdots, \end{align*}

and the total angular momentum, to be denoted by $\vec L \text{,}$ will be

\begin{equation} \vec L = \vec l_1 + \vec l_2 + \cdots + \vec l_N.\tag{9.24} \end{equation}

Subsection 9.6.5 Angular Momentum of a Rotating Rigid Body of Point Masses

Suppose we have $N$ balls tied together by light rigid bars. We can ignore the masses of the bars and focus on the angular momenta of the balls only. Now, this is the same problem as the last subsection --- with one big simplification --- all of the balls have the same angular velocity $\omega\text{.}$

The angular momentum of each of the ball will simply be its moment of inertia times the angular velociy, and the total angular momentum will just be their sum.

\begin{align*} \amp l_1 = m_1 R_1^2 \omega,\\ \amp l_2 = m_2 R_2^2 \omega,\\ \amp l_3 = m_3 R_3^2 \omega,\\ \amp \cdots. \end{align*}

Adding them all, we get the magnitude of the total angular momentum will be

\begin{equation} L = \left( m_1 R_1^2 + m_2 R_2^2 + \cdots + m_N R_N^2 \right)\ \omega,\tag{9.25} \end{equation}

which we can again write as moment of inertia times angular velocity.

\begin{equation} L = I\, \omega,\tag{9.26} \end{equation}

with $I $ for the $N\text{-}$particle system to be

\begin{equation} I = m_1 R_1^2 + m_2 R_2^2 + \cdots + m_N R_N^2.\tag{9.27} \end{equation}

Example 9.43. Angular Momentum of Two Particles Moving in Circles.

Two point particles of masses $m_1$ and $m_2$ are moving uniformly in circles of radii $r_1$ and $r_2$ with the same center in the same direction but on the opposite sides such that the total angular momentum of the two has a constant the magnitude $l_0\text{.}$ The speeds of the two particles are $v_1$ and $v_2$ respectively. Set up a coordinate system so that the particles move in the $xy$-plane and write out components of the angular momenta of the two masses about the center, and show how the two speeds and radii are related.

Answer.

$m_1 v_1 r_1 + m_2 v_2 r_2\text{.}$

Solution.

In this problem the phrase “same direction” is misleading. In rotation this phrase is taken to mean “same sense” when viewed from some reference side.

Figure 9.44 shows the opposite motions of the two particles in the $xy$-plane. Using right-hand rule, we see that angular momentum of both particles are pointed towards $+z$-axis. The magnitudes of the two angular momenta are $m_1 v_1 r_1$ and $m_2 v_2 r_2$ respectively. Therefore, total is

\begin{equation*} l_0 = m_1 v_1 r_1 + m_2 v_2 r_2. \end{equation*}

Subsection 9.6.6 Angular Momentum of a Rotating Rigid Body

The angular momentum of a rotating body depends on angular velocity and moment of inertia, which takes into account how the mass is distributed in the body. In our treatment of angular momentum above, we have noted that if an object is rotating at angular velocity $\omega$ about an axis about which its moment of inertia is $I\text{,}$ then, we could expect its angular momentum to be

\begin{equation} L = I\,\omega.\tag{9.28} \end{equation}

This is true for rotation about special axes, called principal axes. Figure 9.45 and Figure 9.46 illustrate two types of principal axes for a disk.

For instance, for a disk of mass $M $ and radius $R\text{,}$ the moment of inertia $I$ for rotation about the axis through the center of the axis and perpendicular to the disk is

\begin{equation} I_\text{disk}^\perp = \frac{1}{2}M\,R^2.\tag{9.29} \end{equation}

This wouldn’t be the case if you were rotating the disk about an axis through the center but lying in the plane of the disk. Then, we will have

\begin{equation} I_{\text{disk}}^\parallel = \dfrac{1}{4}M\,R^2.\tag{9.30} \end{equation}

For a fixed-axis rotation about axis in Figure 9.45, angular momentum will be in the same direction as angular velocity with magnitude

\begin{equation*} L = \frac{1}{2}M\,R^2\,\omega. \end{equation*}

For a fixed-rotation about axis in Figure 9.46, angular momentum will be in the same direction as angular velocity with magnitude

\begin{equation*} L = \frac{1}{4}M\,R^2\,\omega. \end{equation*}

In general, our axis of rotation, may be in some arbitrary direction. What happens then? Figure 9.47 shows rotation of a disk about an arbitrary axis. We choose Cartesian axes along principal axis of Figure 9.46 and Figure 9.45. Angular momentum vector will be

\begin{equation*} \vec \omega = \omega_x\hat i + \omega_y\hat j+ \omega_z\hat k. \end{equation*}

Now, angular momentum will have the following components

\begin{gather*} L_x = I_{\text{disk}}^\parallel\, \omega_x.\\ L_y = I_{\text{disk}}^\parallel\, \omega_y.\\ L_z = I_\text{disk}^\perp\, \omega_z. \end{gather*}

Clearly, $\vec L$ is not in the same direction as angular velocity $\vec \omega\text{.}$ This is very different than what happened in the case of velocity and momentum - they are always in the same direction.

Example 9.48. Angular Momentum of a Rotating Disk with a Blob Stuck to it.

A disk of mass $M$ and radius $R$ has a blob of mass $m$ stuck at a distance $a$ from the center. The disk with blob rotates about an axle through the center of the disk at an angular speed of $\omega\text{.}$ What is the angular momentum?

Answer.

$\left( \frac{1}{2}MR^2 + m a^2\righty)\,\omega\text{.}$

Solution.

We can do it two ways: (1) Find angular momentum of the disk and the blob separatey and add them vectortially; here, since both angular momenta point inthe same direction, they will add simple. (2) Find the moment of inertia of the disk plus blob and then just multiply it with the angular speed.

Method (1): Let $z$ axis be the axis of rotation. Then, angular momenta has only $z$-component.

\begin{align*} \amp L_{\texxt{disk},z} = I_\texxt{disk}\omega = \frac{1}{2}MR^2\omega.\\ \amp L_{\texxt{blob},z} = I_\texxt{blob}\omega = m a^2\omega.\\ \amp L_{\text{tot},z} = \left( \frac{1}{2}MR^2 + m a^2\righty)\,\omega. \end{align*}

Exercises 9.6.7 Exercises

1. Angular Momentum of a Baton with Heavy Masses at the Ends Rotating in a Plane.

A baton of length $b$ has two balls of mass $m$ at the ends. The mass of the connecting rod is negligible compared to $m\text{.}$ The baton is spinning at a constant angular speed $\omega$ keeping the mid-point of rod fixed while the masses move in a plane. Let the coordinate system $Oxyz$ be chosen so that the origin is at the middle of baton, and the $xy$-plane is the plane in which balls move, and the balls are on the $x$-axis at time $t=0\text{.}$ Write expressions for for an arbitrary time $t\text{:}$

the position vectors of the two masses
the momentum of the two masses,
the total momentum,
the angular momentum of the individual masses,
the total angular momentum.

You should find that even when total momentum is zero, the total angular momentum is not zero!

Solution 1. a

The position vectors $\vec r_1(t)$ and $\vec r_2(t)$ at an arbitrary time will be

\begin{align*} \vec r_1 (t) \amp = \frac{b}{2}\cos(\omega t) \hat u_x + \frac{b}{2}\sin(\omega t) \hat u_y.\\ \vec r_2 (t) \amp= -\vec r_1 (t) \\ \amp = -\left[ \frac{b}{2}\cos(\omega t) \hat u_x + \frac{b}{2}\sin(\omega t) \hat u_y \right]. \end{align*}

We can verify the positions at $t=0$ and the directions of the velocities of the two masses by setting $t=0\text{.}$

\begin{align*} \amp \vec r_1 (0)= \frac{b}{2}\hat u_x;\ \ \vec v_1 (0)=\frac{b\omega}{2}\hat u_y.\\ \amp \vec r_2 (0)= -\frac{b}{2}\hat u_x;\ \ \vec v_2 (0)=-\frac{b\omega}{2}\hat u_y. \end{align*}

Solution 2. b

The momenta of the two particles are

\begin{align*} \amp \vec p_1 = m_1\frac{d}{dt} \vec r_1 (t) = -\frac{mb\omega}{2}\sin(\omega t) \hat u_x + \frac{mb\omega}{2}\cos(\omega t) \hat u_y.\\ \amp \vec p_2 = m_2\frac{d}{dt}\vec r_2 (t) = \frac{mb\omega}{2}\sin(\omega t) \hat u_x - \frac{mb\omega}{2}\cos(\omega t) \hat u_y. \end{align*}

Solution 3. c

The total momentum of the two masses will be zero since the two masses have momenta of equal magnitude but in the opposite directions.

Solution 4. d

The angular momenta of the individual masses are

\begin{align*} \amp \vec L_1 = \vec r_1 \times \vec p_1 = \frac{mb^2\omega}{4}\hat u_z.\\ \amp \vec L_2 = \vec r_2 \times \vec p_2 = \frac{mb^2\omega}{4} \hat u_z. \end{align*}

Solution 5. e

The total angular momentum is

\begin{equation*} \vec L_{\textrm{net}} = \vec L_1 + \vec L_2 = \frac{mb^2\omega}{2} \hat u_z. \end{equation*}

This exercise shows that even when the total momentum is zero, the total angular momentum may not be zero.

2. Angular Momentum of a Baton with Heavy Masses at the Ends Rotating in 3-D Space.

Same baton, same mass as Exercise 9.6.7.1, except this time the baton is spinning so that the plane containing the balls changing with time as shown in Figure 9.50. Let the connecting rod make an angle $\theta$ with the $z$-axis. Find the same things as in Exercise 9.6.7.1.

Solution 1. a

We choose a coordinate system as shown in Figure 9.51 with the origin at the middle of the baton as above, but now the two masses move in planes which are parallel to the $z=0$ plane in circles which have a different radius than before. Let the radius of the circles be denoted by $R$ which is given by

\begin{equation*} R = \frac{b}{2}\sin\theta, \end{equation*}

and the position vectors $\vec r_1(t)$ and $\vec r_2(t)$ at an arbitrary time will be

\begin{align*} \amp \vec r_1 (t) = R\cos(\omega t) \hat u_x + R\sin(\omega t) \hat u_y+ \frac{b}{2} \cos\theta\hat u_z\\ \amp \vec r_2 (t) = -\vec r_1(t). \end{align*}

Solution 2. b

The momentum here will be given by an expression similar to the ones obtained above with $R$ replacing the $b/2$ in the answer in the last question.

\begin{align*} \amp \vec p_1 = m_1\frac{d}{dt} \vec r_1 (t) = -mR\omega\sin(\omega t) \hat u_x + mR\omega\cos(\omega t) \hat u_y. \\ \amp \vec p_2 = m_2\frac{d}{dt}\vec r_2 (t) = -\vec p_1. \end{align*}

Solution 3. c

$\vec p_{\textrm{net}} = 0\text{.}$

Solution 4. d,e

The total angular momentum will not be in the direction of the $z$-axis now. The angular momentum of mass $m_1$ will be

\begin{align*} L_1 \amp = \vec r_1 \times \vec p_1 \\ \amp = \left| \begin{array}{lll} \hat u_x \amp \hat u_y \amp \hat u_z\\ mR\omega\sin(\omega t) \amp mR\omega\cos(\omega t) \amp 0 \end{array} \right|\\ \amp =\frac{mRb\omega}{2} \cos\theta \left[ - \cos(\omega t) \hat u_x +\sin(\omega t) \hat u_y \right] + mR^2\omega \hat u_z. \end{align*}

The angular momentum of $m_2$ is equal to the angular momentum of $m_1$ as we can see from

\begin{equation*} \vec L_2 = \vec r_2 \times \vec p_2 = - \vec r_1 \times (-\vec p_1) = \vec r_1 \times \vec p_1 = \vec L_1. \end{equation*}

Therefore, the total angular momentum will be

\begin{equation*} \vec L_{\textrm{net}} = \vec L_1 +\vec L_2 = 2 \vec L_1. \end{equation*}

3. Angular Momentum of a Three-Particle System Rotating About Different Axes.

Three particles of masses $m_1$, $m_2$ and $m_3$ are tied together by light rods as shown in rotating Figure 9.52. Find its angular momentum with respect to different axes, one shown in (a) Figure 9.52 and the other shown in (b) Figure 9.53.

Solution 1. a

Only $m_2$ is not on the axis of rotation. From the figure, we find that it is rotating in a circle of radius $a\sin\theta\text{.}$ Hence, its angular momentum is

\begin{equation*} L = m_2 (a\sin\theta)^2. \end{equation*}

Solution 2. b

Now, two masses are not on the axis. The mass $m_1$ is going in a circle of radius from top corner to the axis, which we need to figure out from the geometry; let’s call it $r_1$ as shown in Figure 9.54. And mass $m_3$ is going in radius $r_3 = a\cos\theta\text{.}$ From bigger right angled triangle and a smaller right angled triangle show that

\begin{equation*} r_1 = \frac{a}{2}\left( -\cos\theta + \sqrt{1 + 3\sin^2\theta}\right). \end{equation*}

Check this, I might have made an error in calculation. From these we get angular momentum to be

\begin{equation*} \left( m_1r_1^2 + m_3 r_3^2 \right)\, \omega. \end{equation*}

Prev Top Next