Thermal Equilibration Process

Section 23.4 Thermal Equilibration Process

Subsection 23.4.1 Newton’s Law of Cooling

It is a common experience that a hot cup of water placed in a room temperature environment cools down, and eventually the temperature of the cup reaches the room temperature. The heat loss in this process is primarily due to the conduction and convection.

Newton’s cooling states that the temperature of the body \(T(t)\) drops exponentially with time. Let \(T(t)\) be the temperature at instant \(t\) and \(T_0 \) be the ambient temperature. Then, the difference \(T(t) - T_0\) is given by

\begin{equation} T(t) - T_0 = (T(0) -T_0 )\, e^{-\alpha t},\tag{23.16} \end{equation}

where \(\alpha\) is the rate constant of cooling and \(T(0) \) is the initial temperature of the body. Figure 23.17 shows that larger \(\alpha\) means faster cooling.

Figure 23.17. Newton’s law of cooling illustrated for two different values of \(\alpha\text{.}\) The upper curve has \(\alpha= 0.01\ \text{sec}^{-1}\) and the lower curve has \(\alpha = 0.02 \ \text{sec}^{-1}\text{.}\) The larger \(\alpha\) corresponds to faster cooling. Both samples starting at \(80^{\circ}\text{C}\) reach the ambient temperature \(20^{\circ}\text{C}\) asymptotically.

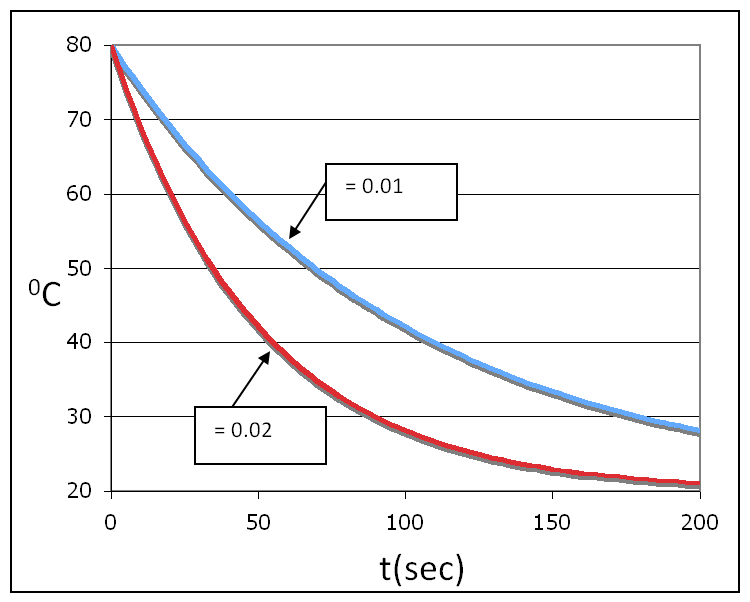
Example 23.18. Time for Cooling a Cup of Coffee.

A 100 ml of coffee at temperature \(75^{\circ}\text{C}\) is placed on a table in an environment that has a constant temperature of \(25^{\circ}\text{C}\text{.}\) It is found that the temperature of the cup after 3 minutes is \(60^{\circ}\text{C}\text{.}\) Find Newton’s rate constant of cooling \(\alpha\text{.}\)

Answer.

\(0.12\ \text{per}\ \text{min} \text{.}\)

Solution.

Since the cooling is primarily due to convection by air in the room, Newton’s law of cooling is applicable. Rearranging the equation given above and then taking a natural log we can bring the exponent down.

\begin{equation*} \ln{\left[ \dfrac{T(t)-T_0}{T(0)-T_0} \right]} = \ln{\left[ \exp{(-\alpha t)}\right]} \end{equation*}

Therefore,

\begin{equation*} \alpha = -\dfrac{1}{t}\ln{\left[ \dfrac{T(t)-T_0}{T(0)-T_0} \right]} \end{equation*}

Now, we put the given values: \(t = 3\ \text{min}\text{,}\) \(T(t) = 60^{\circ}\text{C}\text{,}\) \(T(0) = 75^{\circ}\text{C}\text{,}\) \(T_0 = 25^{\circ}\text{C}\text{,}\) to obtain the value of the rate of cooling \(\alpha\text{.}\)

\begin{equation*} \alpha = -\dfrac{1}{3\ \text{min}}\ln{\left[ \dfrac{60-25}{75-25} \right]} = 0.12\ \text{per}\ \text{min}. \end{equation*}

Subsection 23.4.2 (Calculus) By Conduction and Convection

Newton’s law of cooling can be also written in terms of the rate of cooling, \(dT/dt\text{.}\)

\begin{equation} \dfrac{dT}{dt} = -\alpha\left( T - T_0\right), \tag{23.17} \end{equation}

where \(\alpha\) is the rate constant of cooling. The negative on the right side ensures that the temperature of the hot body will be decreasing with time. Given an initial temperature, \(T(0)\) of the body, we can predict the temperature at a later time by solving this equation which result in the following solution.

\begin{equation} T(t) = \left[T(0) -T_0 \right]\exp{(-\alpha t)} + T_0. \label{}\tag{23.18} \end{equation}

Therefore, we say that the, according to Newton’s law of cooling, the temperature of a hot body placed in a lower temperature environment, drops exponentially. The rate constant \(\alpha\) depends on the conductivity of the container and other conditions, such as air draft. The solution is plotted in Figure 23.17 for two different values of the cooling rate constant to illustrate the role of \(\alpha\) in the rate at which the temperature drops.

Subsection 23.4.3 (Calculus) Heating and Cooling by Radiation

When heat is either gained or lost from a body primarily due to radiation, the rate is not given by Newton’s cooling law. Instead we must use Stefan-Boltzmann equation for deducing the law of rate of cooling due to radiation alone.

As an example, consider an object of emissivity \(\epsilon\) at temperature \(T\) in outer space. We assume that the energy received by the body is negligible compared to the energy radiated out. Stefan-Boltzmann says that the body will radiate out energy at the following rate.

\begin{equation} P = \epsilon\sigma A T^4, \tag{23.19} \end{equation}

where \(A\) is the surface area and \(\sigma\) the Stefan-Boltzmann constant. The energy loss will result in a decrease in temperature given by the relation of heat to temperature by way of specific heat, \(c\text{.}\)

\begin{equation} P = -\dfrac{dQ}{dt}= -mc \dfrac{dT}{dt}\ \ \ (dT/dt \lt 0), \tag{23.20} \end{equation}

where negative sign is included to indicate the energy loss with increasing time.

For simplicity in writing we do not distinguish the specific heat into the constant volume, constant pressure, or some other process. If we neglect any effect due to expansion or contraction of the sample, a more appropriate specific heat will be the constant volume specific heat. Equating the two rates, viz. the emitted rate from Eq. (23.19) and the loss of energy rate from Eq. (23.20), we find the required law for temperature change of the body when the body loses energy solely due to the radiation.

\begin{equation*} \dfrac{dT}{dt} =-\dfrac{ \epsilon\sigma A}{mc} T^4 \ \ \text{(solely due to radiation.)} \end{equation*}

Integrating this equation from \([t=0, T(0)]\) to \([t, T(t)]\text{,}\) we find the temperature at arbitrary time is given by the following complicated formula.

\begin{equation} T(t) = \left[\dfrac{1}{T(0)^3} + \dfrac{3\epsilon\sigma A}{mc}t \right]^{-1/3}. \tag{23.21} \end{equation}

Example 23.19. Cooling a Copper Spherical Ball by Radiation.

A copper spherical ball of radius 5 cm is heated to a temperature \(150^{\circ}\)C and hung by a non-conducting wire in a vacuum chamber whose walls are kept cold at very low temperature so that the energy received by the copper ball by radiation is negligible compared to the energy emitted by the ball. Find the temperature of the ball after 10 minutes. Use specific heat of copper to be 379 J per Kg per degree K, and density of copper to be \(8230\text{ kg/m}^3\text{.}\) Assume emissivity 1 for the copper ball.

Answer.

\(416\text{K} \)

Solution.

We use the following values in Eq. (23.21).

\begin{align*} \amp \epsilon = 1, \\ \amp T(0) = 150+273.15 = 423.15\ \text{K}, \\ \amp A = 4\pi R^2 = 4\pi (0.05\text{m})^2 = 0.0314\ \text{m}^2, \\ \amp \sigma = 5.7\times 10^{-8} \text{W/m}^2\text{K}^4, \\ \amp m = \rho V = (8230\ \text{kg/m}^3) \times \dfrac{4}{3}\pi (0.05\text{m})^3 = 12.93\ \text{kg}, \\ \amp t = 600 \text{sec}. \end{align*}

Therefore, the temperature of the ball after 30 seconds is

\begin{align*} \amp a = \dfrac{3\times 1\times 5.7\times 10^{-8}\times 0.0314}{12.93\times 379}\times 600,\\ \amp = 1.09569 \times 10^{-12},\\ \amp T(t) = \left[ \dfrac{1}{423.15^3} + a \right]^{-1/3} = 416\ \text{K}. \end{align*}

Need to be careful with roundoff errors here.

Example 23.20. Radiation Transfer in a Spherical Cavity.

Consider a spherical cavity kept at temperature \(T_1\) that has a spherical ball which is maintained at temperature \(T_2\) with \(T_1>T_2\) (Fig. \ref{fig:example-radiation-sphere}). We wish to find the rate at which heat will be transferred from 1 to 2 by radiation mechanism. Note that the temperature of the ball inside the cavity will rise.

Assume that inside the ball there is a mechanism for taking the heat out so that its temperature does not rise. Similarly, assume that there is a mechanism for continuously supplying energy to the cavity so that its temperature is also kept at \(T_1\text{.}\) Let the surface areas of 1 and 2 be \(A_1\) and \(A_2\) respectively. Let \(\epsilon_1\) and \(\epsilon_2\) be their emissivities. Also, assume emissivity and absorptivity of the ball are equal.

Solution.

We can work out the transfer of heat through radiation by looking at the surface that will be absorbing the heat, which in the present case is the ball. In time \(\Delta t\text{,}\) the ball will absorb radiation from the cavity and will also emit some radiation, the difference of which will be the amount of heat transferred.

\begin{equation*} \text{Energy absorbed - Energy emitted} = A_2\epsilon_2\epsilon_1\sigma T_1^4\Delta t - A_2\epsilon_2\sigma T_2^4\Delta t \end{equation*}

Hence the rate of transfer of heat from 1 to 2 through radiation is given as follows.

\begin{equation*} \dfrac{\Delta Q}{\Delta t} = A_2\epsilon_2\sigma\left( \epsilon_1 T_1^4 - T_2^4\right) \end{equation*}

Prev Top Next