The CM Frame

Section 7.8 The CM Frame

You saw above that total momentum, or equivalently center-of-mass momentum does not change during a collision. That suggests that a reference frame attached to the center of mass would also be an inertial frame. This frame is called the CM frame. Calculations become simpler when performed in this frame. Once, you have made calculations in the CM frame, you can deduce the results in the regular or lab frame by the associated transformations.

Consider a block A moving towards another block B at rest on a table as shown in Figure 7.89. The left side of the figure shows the drawing in standard frame, called LAB frame. The CM of the two blocks also moves towards B here, but at a lower speed than speed of A.

The first row in Figure 7.89 is the situation before the collision and the bottom part is the situation after the collision. The left two figures illustrate that momentum is conserved in the collision; the total momentum given by total mass times the CM velocity does not change in collision.

The right two figures in Figure 7.89 show the same situation in the CM frame. In the CM frame, the origin is at the CM. In this frame, both A and B have non-zero velocity. Before the collision, they are moving towards origin with momentum of equal magnitude and opposite direction.

\begin{equation*} \vec p_{A,\text{cm}} + \vec p_{B,\text{cm}} = 0. \end{equation*}

That is,

\begin{equation*} m_A\vec v_{A,\text{cm}} + m_B\vec v_{B,\text{cm}} = 0. \end{equation*}

After collision, they are moving away from CM, again with momentum of equal magnitude and opposite direction.

\begin{equation*} \vec p'_{A,\text{cm}} + \vec p'_{B,\text{cm}} = 0. \end{equation*}

That is,

\begin{equation*} m_A\vec v'_{A,\text{cm}} + m_B\vec v'_{B,\text{cm}} = 0. \end{equation*}

Because of the symmetry in the before and after collision, as observed in the CM frame, this frame is often used to study collision problems.

Subsection 7.8.1 Relation between CM and LAB frames

Relating LAB and CM frames is no different than relating any two inertial frames as we have studied in the relative velocity section. Suppose we want to find the relation for position, velocity and acceleration between LAB and CM frames.

Let \(\vec R\) be the position of the origin of the CM frame with respect to the origin of the LAB frame. Let \(\vec r\) and \(\vec r_\text{cm}\) be position of a particle with respect to the origins of the LAB and CM frames respectively. Then, from traingle of vectors we will have

\begin{equation} \vec r = \vec R + \vec r_\text{cm}.\tag{7.83} \end{equation}

Here, \(\vec r\) and \(\vec R\) are in the LAB frame and \(\vec r_\text{cm}\) is in the CM frame. The quantities \(\vec r\) and \(\vec r_\text{cm}\) are positions of the same point particle with respect to the LAB and CM frames respectively and \(\vec R\) is the position of the CM in the LAB frame. Now, by taking a time derivative we immediately get the relation among velocities.

\begin{equation} \vec v = \vec V + \vec v_\text{cm}.\tag{7.84} \end{equation}

Another derivative gives us relation among the accelerations.

\begin{equation} \vec a = \vec A + \vec a_\text{cm}.\tag{7.85} \end{equation}

Once again, in these relations \(\vec R\text{,}\) \(\vec V\text{,}\) and \(\vec A\) are the position, velocity, and acceleration of the CM as observed in the LAB frame; they are, of course, all zero in the CM frame since origin of the CM frame moves with the CM itself.

Subsection 7.8.2 Velocities in CM and LAB Frame of Two Bodies

Let \(m_A\) and \(m_B\) be the masses of two bodies A and B with velocities \(\vec v_{A,\text{cm}}\) and \(\vec v_{B,\text{cm}}\) in the CM frame and \(\vec v_{A,\text{LAB}}\) and \(\vec v_{B,\text{LAB}}\) in the LAB-frame. In the LAB frame, we can easily see that the velocity of CM itself with respect to the LAB frame, to be denoted as \(\vec V\text{,}\) will be

\begin{equation*} \vec V = \frac{ m_A\vec v_{A,\text{LAB}} + m_B\vec v_{B,\text{LAB}} }{m_A + m_B} \end{equation*}

Now, we can use Eq. (7.84), to write the relation between LAB and CM velocities of the two bodies.

\begin{align} \amp \vec v_{A,\text{LAB}} = \vec V + \vec v_{A,\text{cm}}, \tag{7.86}\\ \amp \vec v_{B,\text{LAB}} = \vec V + \vec v_{B,\text{cm}}.\tag{7.87} \end{align}

Subsection 7.8.3 Collision in CM Frame

Above in Figure 7.89 we found that in the CM frame, both particles appraoch the CM with equal magnitude momentum and after collision move away with some other magnitude momentum, again both with equal magnitude.

In two or more dimensions, the directions of the menenta of the two bodies are still along the same line, but the line of the motions of the two bodies may be different than the line they approached the CM before the collision. That is, there is a rotation of the direction of motion in the collision process as shown in Figure 7.91. Still the outgoing directions and incoming directions fall into one Cartesian plane!

In Figure 7.91, we will have the following relation for the conservation of momentum in the collision process, noting that net momentum in CM frame is zero.

\begin{equation*} m_A \vec v'_{A,\text{cm}} + m_B \vec v'_{B,\text{cm}} = m_A \vec v_{A,\text{cm}} + m_B \vec v_{B,\text{cm}} = 0. \end{equation*}

The angle of rotation of direction can be obtained from looking at the ratio of \(x\) and \(y\) components of \(\vec v'_{A,\text{cm}}\) or \(\vec v'_{B,\text{cm}}\text{.}\)

\begin{equation*} \tan\,\theta = \frac{v'_{B,\text{cm},y}}{v'_{B,\text{cm},x}}. \end{equation*}

Example 7.92. Scattering of Alpha Particles from Gold Nucleus.

Alpha particles of mass \(4\, \text{AMU}\) are incident on gold nucleus of mass \(197\,\text{AMU}\text{.}\) Before the collision, alpha particle is moving with a speed of \(2\times10^5\ \text{m/s}\) in the LAB-frame. After the collision, the alpha particle comes out with a speed of \(1.5\times10^5\ \text{m/s}\) at an angle of \(10^{\circ}\) from the original direction in the LAB frame. Find the angle between the incoming and outgoing directions in the CM-frame. AMU is atomic mass unit with value \((1\ \text{AMU} = 1.66053\times10^{-27} \text{ kg})\text{.}\)

Answer.

\(10^\circ\text{.}\)

Solution.

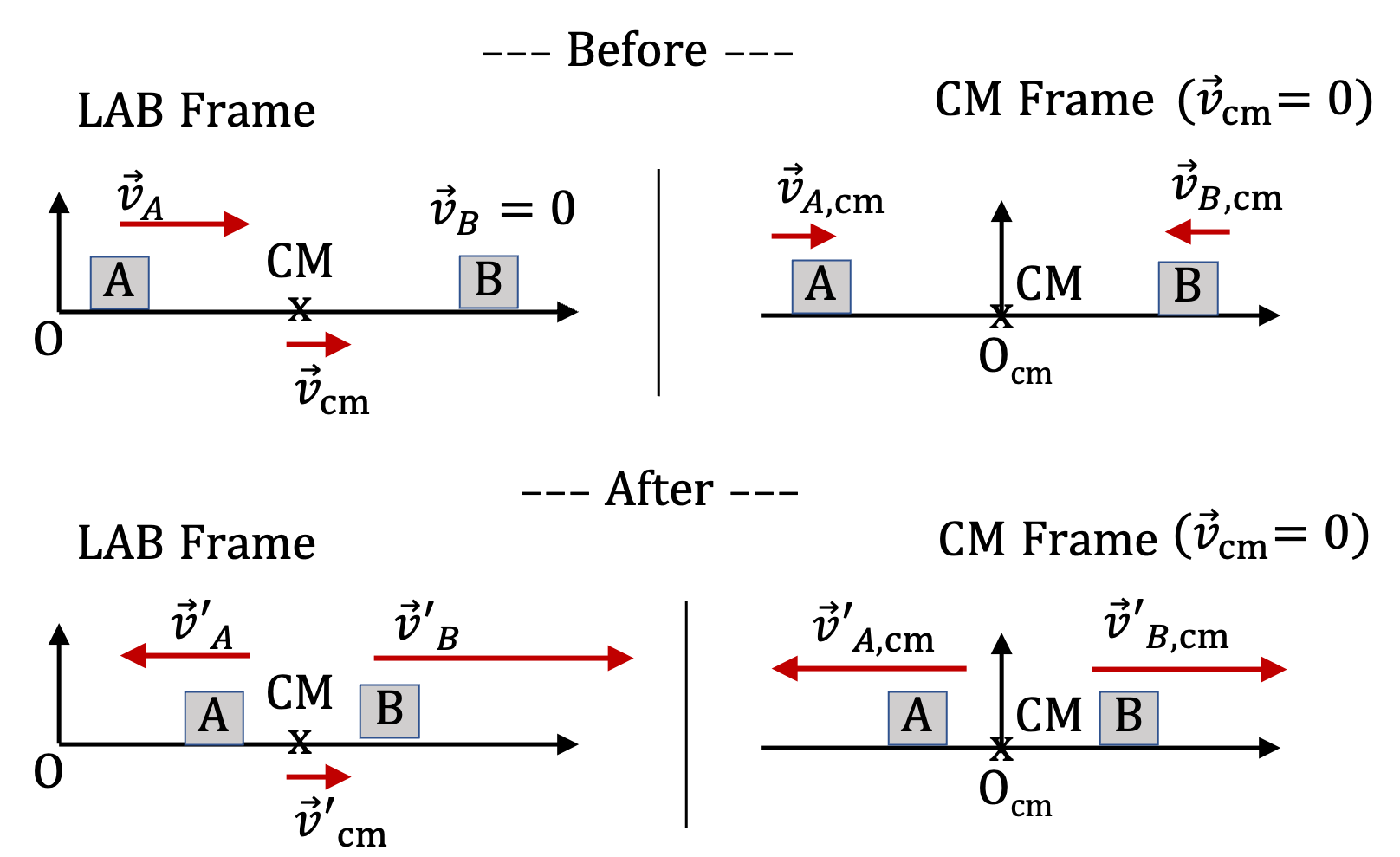
Let us orient axes of the LAB and CM frames so that their axes are parallel, and initially the motion is along the \(x\)-axis as in Figure 7.91. The velocity of the origin of the CM-frame with respect to the LAB-frame will be towards positive \(x\)-axis. Only \(V_x\) will be non-zero.

\begin{equation*} V_{x} = \frac{4 \times 2 \times 10^5 + 0}{4+197} = 4,000 \text{m/s}. \end{equation*}

Let \(v_x\) and \(v_y\) denote the velocity (in LAB frame) of gold nucleus after collision. Conservation of momentum in LAB frame gives

\begin{gather*} 4\times 1.5\times10^5\, \cos(10^\circ) + 197\times v_x = 4\times 2 \times 10^5.\\ 4\times 1.5\times10^5\, \sin(10^\circ) +197\times v_y = 0. \end{gather*}

Therefore,

\begin{equation*} v_x = 1,061.5,\ \ v_y = -529. \end{equation*}

Now, we can compute velocities of alpha particle and gold nucleus in CM frame by subtracting the velocity of CM from these numbers.

\begin{align*} \amp\text{Gold nucleus: } v_{x,\text{cm}} = 1,061.5-4,000 = -2938.5,\ \ v_{y,\text{cm}} = -529\\ \amp\text{alpha: } v_{x,\text{cm}} = 147,721-4,000 = 143,721,\ \ v_{y,\text{cm}} = 26,047. \end{align*}

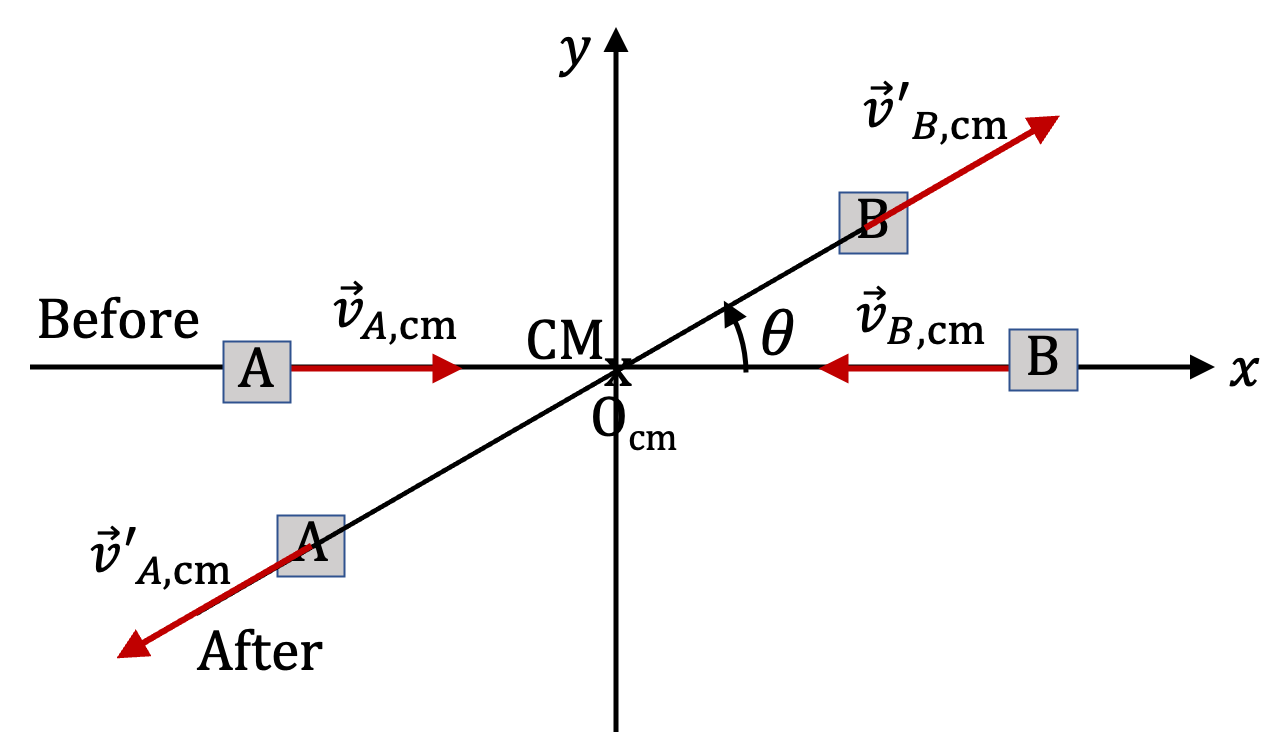
Therefore, angle between incoming and outgoing directions is

\begin{equation*} \tan^{-1}\frac{-529}{2938.5} = 10^\circ,\text{ counterclockwise from }-x\text{-axis}. \end{equation*}

or,

\begin{equation*} \tan^{-1}\frac{26,047}{143,721} = 10^\circ,\text{ counterclockwise from +}x\text{-axis}. \end{equation*}

Prev Top Next