Skip to main content
   
Logo image

Physics Bootcamp

Samuel J. Ling

Section 37.7 Magnetic Materials Bootcamp

Exercises Exercises

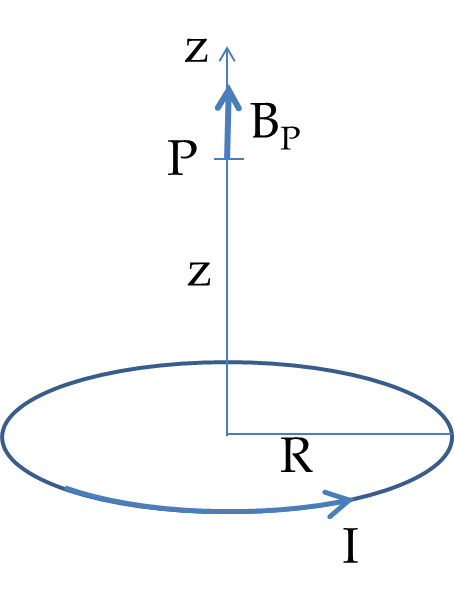
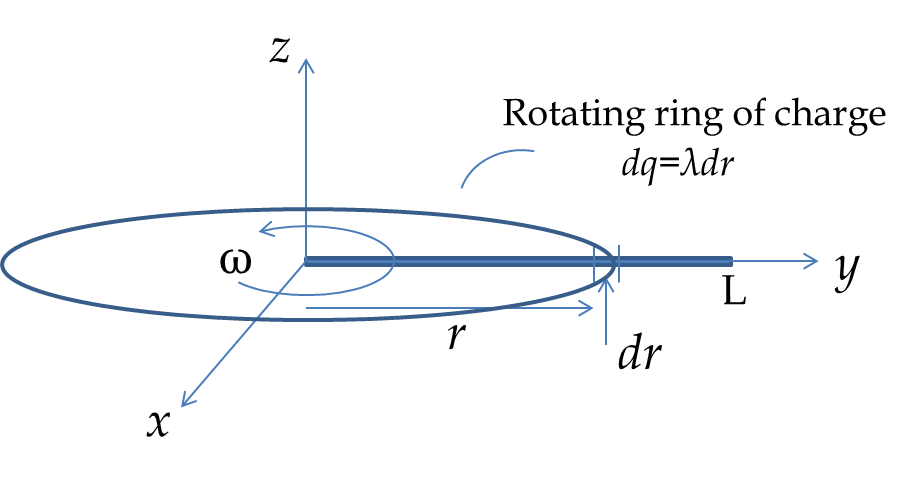
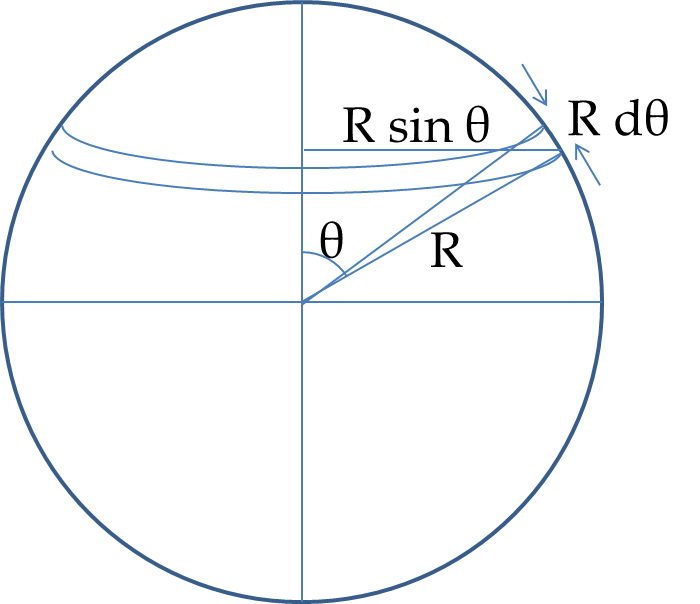
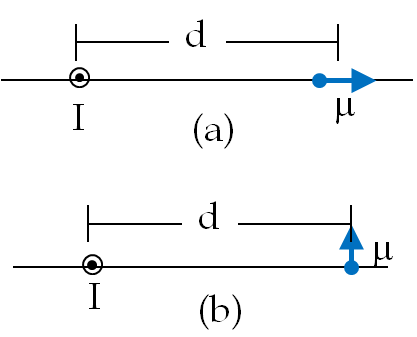
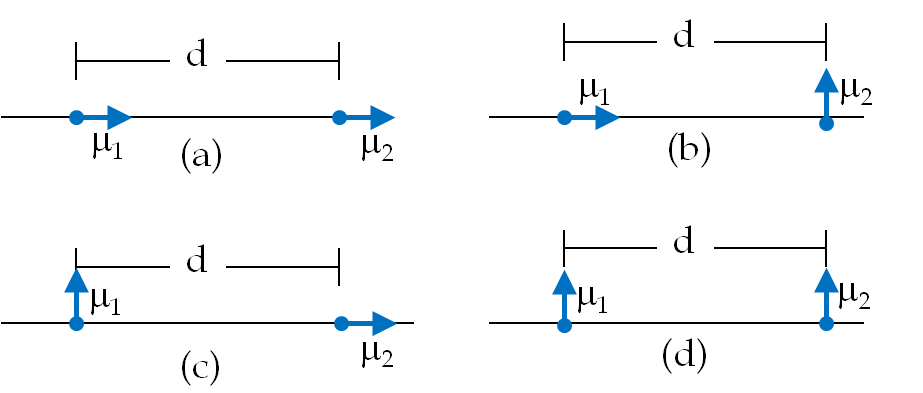
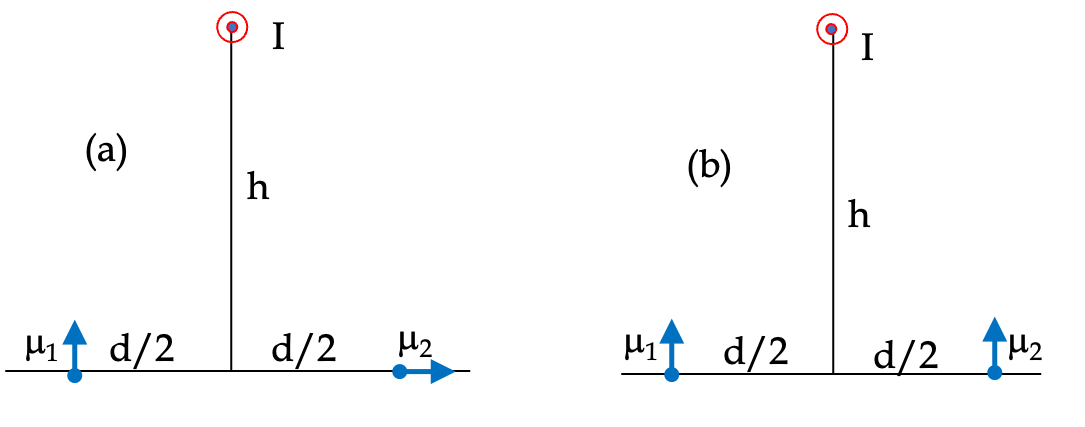
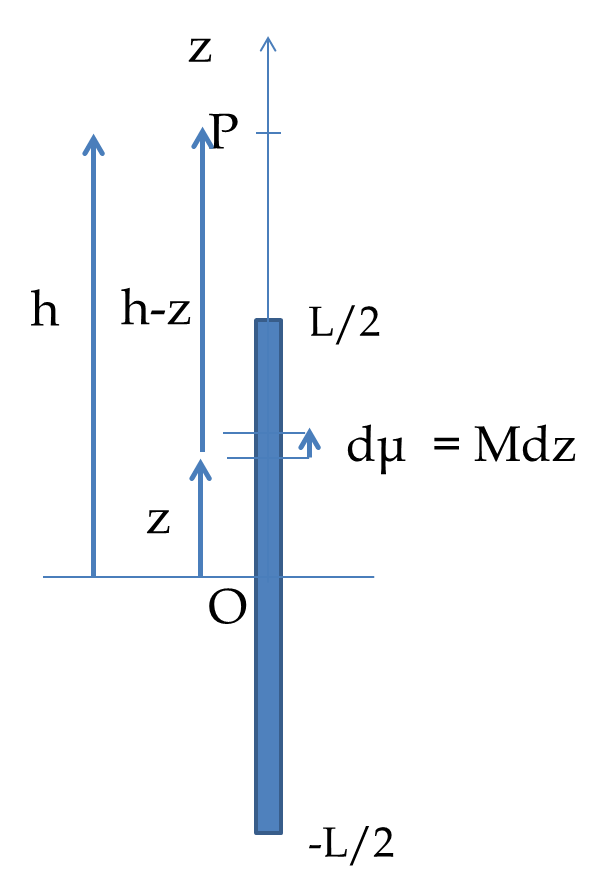
Magnetic Dipoles

2. Rotating a Nuclear Magnetic Dipole in a Magnetic Field.
Follow the link: Exercise 37.1.5.2.
3. Torque on a Magnetic Dipole and Energy Required to Flip its Orientation.
Follow the link: Exercise 37.1.5.3.
4. Magnetic Dipole Moment and Equivalent Circulating Current from Torque.
Follow the link: Exercise 37.1.5.4.
5. Force on a Magnetic Dipole in an Nonuniform Magnetic Field of a Bar Magnet.
Follow the link: Exercise 37.1.5.5.
6. Energy for Rotating a Magnetic Dipole by an Arbitrary Angle.
Follow the link: Exercise 37.1.5.6.
7. (Calculus) Force on a Magnetic Dipole in a Nonuniform Magnetic Field Given in Analytic Form.
Follow the link: Exercise 37.1.5.7.
8. Force and Torque on a Magnetic Dipole Placed in a Solenoid.
Follow the link: Exercise 37.1.5.8.
9. Energy for Rotating Magnetic Dipole Moment of Proton.
Follow the link: Exercise 37.4.3.1.

Microscopic View of Magnetic Materials

10. Calculating Magnetic Moments of Atoms.
Follow the link: Example 37.6.
11. Magnetic Moment of a Helium Atom in an Electronically Excited State.
Follow the link: Example 37.7.

Induced Dipole Moments

12. Induced Magnetic Moment in a Helium Atom.
Follow the link: Example 37.9.
13. Induced Magnetic Dipole Moment in Bismuth.
Follow the link: Example 37.10.

Magnetization and Magnetic Field

14. Magnetism in Copper Rod Carrying Current.
Follow the link: Example 37.18.
16. Magnetization of Water from Parallel Currents over its Surface.
Follow the link: Exercise 37.6.4.2.
17. Magnetization of Oxygen Gas by Current in a Wire.
Follow the link: Exercise 37.6.4.3.

Miscellaneous

18. Torque on Currnt in a Rectangular Wire in a Magnetic Field.
A rectangular wire carries a current \(I\) and lies in a uniform magnetic field as shown in Figure 37.19. Find (a) the magnetic dipole moment of the loop of current, (b) torque on loop of current using force on dipole formula, and (c) energy it will take to flip the direction of the magnetic dipole by \(180^{\circ}\text{.}\) (d) Draw the orientation of the loop when the magnetic dipole is flipped by \(180^{\circ}\text{.}\)
Figure 37.19.
Solution 1. a
The magnitude of the magnetic dipole moment has the value \(\mu = \textrm{current} \times \textrm{area}\text{.}\) Here we get \(\mu = Iab\text{.}\) The direction is perpendicular to the plane of the loop and is obtained by using a right-hand rule. In the figure the application of the right-hand rule gives the direction to the right.
Solution 2. b
Since the magnetic dipole moment and the external magnetic field are perpendicular to each other, the magnitude of the torque will simply be the product of the two, \(\tau = \mu\: B_0\:\sin\:90^{\circ} = I ab B_0\text{.}\) The direction of the torque is obtained by the right hand rule for the cross-product \(\vec\mu\times \vec B\text{.}\)
Solution 3. c
Since the original direction of \(\vec\mu\) is \(90^{\circ}\) to \(\vec B\) and the final direction after the flip will also be \(90^{\circ}\) to \(\vec B\text{.}\) That means there would be no net energy change.
Solution 4. d
You could just change the direction of the current.
19. Magnetic Dipole Moment of Current Around an L-Shaped Structure.
(a) Find the direction and magnitude of magnetic dipole moment of a closed loop of current shown in Figure 37.20. (b) There is a uniform magnetic field of magnitude \(B_0\) pointed vertically upward in the region of the loop. Find magnitude and direction of torque on the loop. (c) What is the amount of potential energy of the dipole in the present orientation?
Figure 37.20.
Answer.
(b) Magnitude \(IbcB_0\text{,}\) (c) \(-IbcB_0\text{.}\)
Solution 1. a
(a) Since there are two planar segments in the current loop, we first assign a magnetic dipole moment vector to each planar segment and then add them vectorially to obtain the net magnetic dipole moment of the entire loop. Let \(x\)-axis be pointed to the right, the \(y\)-axis to the up, and the \(z\)-axis in the direction out-of-page. Then one segment will be in the \(xz\)-plane and the other in the \(yz\)-plane. Let the magnetic dipole moments of these segments be denoted by \(\vec \mu_1\) and \(\vec \mu_2\) respectively.
Figure 37.21.
Writing the magnetic dipole moments \(\vec \mu_1\) and \(\vec \mu_2\) in terms of the current and dimensions of the wires we have
\begin{equation*} \vec \mu_1 = I a b\:\hat u_y,\ \ \vec \mu_2 = I bc\:\hat u_x. \end{equation*}
Therefore, the net magnetic dipole moment will have the magnitude
\begin{equation*} \mu = \sqrt{(Iab)^2 +(Ibc)^2} = I b \sqrt{a^2 + c^2}, \end{equation*}
and the direction will be in the \(xy\)-plane given by the angle
\begin{equation*} \theta = \tan^{-1}\left(\dfrac{a}{c} \right) \end{equation*}
with respect to the \(x\)-axis.
Solution 2. b
Since the dipole moment is pointed in the \(xy\)-plane and the magnetic field is pointed along the \(y\)-axis, the torque on the dipole will be pointed along the \(z\)-component with the magnitude
\begin{equation*} |\tau| = |\vec \mu \times B_0 \hat u_y| = \mu_x \:B_0 = I b c B_0. \end{equation*}
The right-hand rule for the cross-product \(\vec \mu \times B_0 \hat u_y\) give the direction of the torque towards the positive \(z\)-axis.
Solution 3. c
The potential energy of a magnetic dipole in an external magnetic field is given by
\begin{equation*} U = -\vec\mu \cdot \vec B = -\mu_y B_0 = -IabB_0. \end{equation*}
20. Magnetic Dipole Moment of a Rotating Ring of Charge.
A thin ring of radius \(R\) has an excess charge \(Q\) on it. The ring is rotated about an axis through the center of the ring and perpendicular to its plane at a uniform angular speed \(\omega\text{.}\) (a) Find the magnitude and direction of the magnetic dipole moment. (b) What is the magnitude and direction of the magnetic field on a point on the axis far away from the ring such that the distance \(z\) of the point from the center of the ring is such that \(|z| \gg R\text{.}\)
Figure 37.22.
Answer.
(a) Magnitude \(\omega Q R^2/2\) (b) Magnitude \(\mu_0\omega Q R^4/4z^3\text{.}\)
Solution 1. a
When the ring rotates the charges rotate with it. Now, suppose you place yourself at the space point somewhere on the circumference of the ring and watch the charges in the ring move past you, you will conclude that there is a current in the ring. We can find the magnitude of the current in the ring by calculating the amount of charge that moves past the point per unit time. Since all the charges in the ring will pass through the point when the ring rotates once, there will be both positive and negative currents and only the excess charges \(Q\) placed will show up as the net current. The time to go around once is equal to \(2\pi/\omega\text{.}\) Therefore, the current \(I\) in the ring will be
\begin{equation*} I = \dfrac{Q}{2\pi/\omega} = \dfrac{\omega\:Q}{2\pi}. \end{equation*}
Multiplying this by the area of the ring gives the magnitude of the magnetic dipole moment
\begin{equation*} \mu = I \pi R^2 = \dfrac{\omega\:Q\:R^2}{2}. \end{equation*}
The direction of \(\vec \mu\) is obtained by using the right-hand rule. Since \(Q\) is positive, the direction of the angular velocity vector \(\vec \omega\) will be the direction of the magnetic dipole moment.
Solution 2. b
The magnetic field of the moving charges in the ring will be same as that of a ring of current \(I\text{.}\) This is obtained by Biot-Savart law with the magnitude
\begin{equation*} B_P = \dfrac{\mu_0\;IR^2}{2(R^2 + z^2)^{3/2}}, \end{equation*}
with direction away from the ring for points above the ring and towards the ring for points below the ring.
Figure 37.23.
Taking \(z \gg R\) limit gives
\begin{equation*} B_P (z \gg R) = \dfrac{\mu_0 I R^2}{2z^3} = \dfrac{\mu_0\omega\:Q\;R^4}{4z^3}. \end{equation*}
21. Magnetic Dipole Moment of a Charged Rotating Rod.
A non-conducting rod of length \(L\) has a uniform charge density \(Q/L\) distributed on it. The rod is then pivoted on one end and rotated at a uniform angular speed \(\omega\text{.}\) Show that the rod will have magnetic dipole moment of magnitude \(\frac{1}{6}\: \omega\: Q\: L^2\text{.}\) Draw a figure and state the direction of the magnetic dipole moment vector.
Solution.
We write \(\lambda\) for charge per unit length \(Q/L\text{.}\) Consider an element of length \(dr\) of the rod with charge \(dq = \lambda dr\text{.}\) These charges rotate around the axis through the end of the rod as shown in Figure 37.24
Figure 37.24.
The charges \(dq\) go around once in a circle of radius \(2\pi r\) in time \(2\pi/\omega\text{.}\) Therefore, we can thing of them as makign a current \(dI\) given by
\begin{equation*} dI = \dfrac{\omega\:dq}{2\pi} = \dfrac{\omega\:\lambda\:dr}{2\pi} \end{equation*}
We can assign a magnetic dipole moment pointed towards the positive \(z\)-axis (in the figure) and magnitude
\begin{equation*} d\mu = dI\: \pi r^2 = \dfrac{\omega\:\lambda}{2}\: r^2\:dr. \end{equation*}
Now, integrating from \(r=0\) to \(r=L\) will sum up the magnetic dipole moments of all moving charges. This will give
\begin{equation*} \mu = \dfrac{\omega\:\lambda}{2}\: \int_0^L\: r^2\:dr = \dfrac{\omega\:\lambda\:L^3}{6} = \dfrac{\omega\:Q\:L^2}{6}. \end{equation*}
The direction would be towards the \(z\)-axis as stated above.
22. Magnetic Dipole Moment and Magnetic Field of Rotating Charged Spherical Shell.
A sphere of radius \(R\) carries a charge \(Q\) uniformly distributed on its surface. The sphere rotates about an axis through its center at an angular speed of \(\omega\text{.}\) (a) Find the magnitude and direction of magnetic dipole moment. (b) Find the magnitude and direction of magnetic field on the axis at a far away point P. (c) Let \(z\) be the axis of rotation, then what is the magnitude and direction of magnetic field at a far away point on the \(xy\)-plane?
Solution 1. a
A rotating spherical surface can be thought of consisting of rings. A ring of radius \(R\sin\:\theta\) and thickness \(Rd\theta\) is shown in the figure. This ring has a charge \(dq = \sigma\times (2\pi R\sin\:\theta)(Rd\theta)\text{,}\) where \(\sigma\) is the charge per unit area on the surface. Here \(\sigma = Q/4\pi R^2\text{.}\)
Figure 37.25.
The magnetic dipole of a rotating ring of charges was evaluated above in another problem. We can write the answer for the ring here by a simple translation of the corresponding quantities. We will denote the magnetic dipole of the ring here as \(d\mu\text{.}\) [Note the direction of \(d\vec\mu\) is towards the axis of rotation since \(dq\) is positive.]
\begin{equation*} d\mu = \dfrac{1}{2}\:\omega\: dq\: (R\sin\:\theta)^2. \end{equation*}
Let us write the \(dq\) here in terms of the more basic quantities so that we an discover the integral we can perform.
\begin{equation*} d\mu = \dfrac{1}{2}\:\omega\: (R\sin\:\theta)^2\: \sigma\times (2\pi R\sin\:\theta)(Rd\theta). \end{equation*}
This identifies the integration variable \(\theta\text{.}\) WE know tht an integration from \(\theta = 0\) to \(\theta = \pi\) will sum over all the rings and will give us the net dipole moment of the current in the rotating sphere.
\begin{equation*} \mu = \pi\:\omega\: \sigma\:R^4 \int_0^{\pi} \sin^3\:\theta d\theta = \dfrac{2}{3}\pi\:\omega\: \sigma\:R^4 = \dfrac{1}{6} \:\omega\: Q\:R^2 .\ \ \ \ (1) \end{equation*}
Solution 2. b
The magnetic field at a far away point can be obtained by replacing the rotating spherical charge by its magnetic dipole moment. The dipole field at a far-away point on the axis of the rotation will be
\begin{equation*} B_P (z \gg R) = \dfrac{\mu_0\:\mu}{2\pi |z|^3}, \end{equation*}
where \(z\) is the coordinate the field point P. Putting \(\mu\) from (1) we get
\begin{equation*} B_P (z \gg R) = \dfrac{1}{12\pi}\dfrac{\mu_0\:\omega\: Q\:R^2}{|z|^3}. \end{equation*}
Solution 3. c
The magnetic field at an arbitrary point from a magnetic dipole moment \(\mu\) at the origin pointed towards the \(z\)-axis is given by
\begin{equation*} \vec B_P = \dfrac{\mu_0\mu}{4\pi r^3}\left( 2\cos\theta\:\hat u_r + \sin\theta\:\hat u_{\theta} \right), \end{equation*}
where \(r\) is the (spherical) radial distance to point P and \(\theta\) is the angle with respect to the positive \(z\)-axis. For a point P on the \(xy\)-plane we will have \(\theta = 90^{\circ}\) and \(\hat u_\theta = -\hat u_z\text{.}\) Therefore,
\begin{equation*} \vec B_P =- \dfrac{\mu_0\mu}{4\pi r^3} \;\hat u_z. \end{equation*}
In the present case we use (1) to write \(\mu\) in this equation. This will give
\begin{equation*} \vec B_P =- \dfrac{1}{24\pi}\dfrac{\mu_0 \:\omega\: Q\:R^2}{r^3} \;\hat u_z, \end{equation*}
where \(r = \sqrt{x^2 + y^2}\) with point P at \((x,y,0)\text{.}\)
23. Force on Dipoles from Magnetic Field of a Current in Straight Wire.
Find the force on a dipole \(\vec \mu\) from a current \(I\) in a long straight wire in each of the cases shown in Figure 37.26.
Figure 37.26.
Solution 1. both
With potential energy \(U = -\vec\mu\cdot\vec B\text{,}\) we obtain the formula for the force on the dipole to be
\begin{equation*} \vec F = \hat u_x\: \dfrac{\partial U}{\partial x} + \hat u_y\: \dfrac{\partial U}{\partial y} + \hat u_z\: \dfrac{\partial U}{\partial z}.\ \ \ \ (1) \end{equation*}
In the present problem, the magnetic field at the location of the dipole is generated by the current \(I\text{.}\) We have already obtained the general expression of the magnetic field of current in a straight wire. The expression is written for a point P that is a distance \(s\) away from the wire. Writing the direction of the magnetic field in terms of the unit vector \(\hat u_{\phi}\text{,}\) which is tangent to a circle around the wire.
\begin{equation*} \vec B = \dfrac{\mu_0 I}{2\pi}\:\dfrac{1}{s}\:\hat u_{\phi}. \end{equation*}
Writing this in terms of Cartesian coordinates we get
\begin{equation*} \vec B = \dfrac{\mu_0 I}{2\pi}\: \left[ - \dfrac{y}{x^2+y^2}\:\hat u_{x} + \dfrac{x}{x^2+y^2}\:\hat u_{x}\right].\ \ \ \ (2) \end{equation*}
Solution 2. a
Here
\begin{equation*} \vec \mu = \mu\:\hat u_x,\ \ \ \ \ \ \ (3) \end{equation*}
where \(\mu\) is the magnitude of the magnetic dipole moment. Therefore, putting (2) and (3) in (1) we get
\begin{equation*} \vec F = \dfrac{\mu_0 \: \mu\: I}{2\pi}\: \left[ -\hat u_x\: \dfrac{\partial}{\partial x} \left(\dfrac{y}{x^2+y^2} \right) + \hat u_y\: \dfrac{\partial}{\partial y} \left(\dfrac{y}{x^2+y^2} \right)\right]. \end{equation*}
After we carry out the differentiations, we will set \(x=d\) and \(y=0\) for the coordinates of the location of the dipole. This gives
\begin{equation*} \vec F = \dfrac{\mu_0 \: \mu\: I}{2\pi\: d^2}\: \: \hat u_y. \end{equation*}
Solution 3. b
Here
\begin{equation*} \vec \mu = \mu\:\hat u_y.\ \ \ \ \ (4) \end{equation*}
Therefore, putting (3) and (4) in (1) we get
\begin{equation*} \vec F = \dfrac{\mu_0 \: \mu\: I}{2\pi}\: \left[ \hat u_x\: \dfrac{\partial}{\partial\: x} \left(\dfrac{x}{x^2+y^2} \right) + -\hat u_y\: \dfrac{\partial}{\partial\: y} \left(\dfrac{x}{x^2+y^2} \right)\right]. \end{equation*}
After we carry out the differentiations, we will set \(x=d\) and \(y=0\) for the coordinates of the locaiton of the dipole.
\begin{equation*} \vec F = - \dfrac{\mu_0 \: \mu\: I}{2\pi}\: \: \hat u_x. \end{equation*}
24. Force Between Magnetic Dipoles.
Find the force on dipole \(\vec\mu_2\) from \(\vec\mu_1\) in Figure 37.27.
Figure 37.27.
Hint.
Use the general formula for the magnetic field of one dipole, say from one, and take a dot product of this field with the dipole moment of the other. Then take the derivatives of the negative of the dot product as done in the last problem, Exercise 37.7.23.
25. Force on a Current Carrying Wire by Magnetic Dipoles.
Refer to Figure 37.28 where magnetic dipoles are fixed in their positions. Find the force per unit length on the current carrying wire on a small section of a long wire passing through the plane.
Figure 37.28.
Hint.
Find the force between \(I\) and \(\mu_1\) and \(I\) and \(\mu_2\text{.}\) Use superposition of these forces.
26. Work to Bring two Magnetic Dipoles near Each Other.
Find the work done in bringing two dipoles from infinity and rotating them to the orientation shown in Figure 37.29.
Figure 37.29.
Hint.
Find the energy by \(-\vec \mu_1\cdot\vec B_2\text{,}\) where \(\vec B_2\) is the field of \(\vec \mu_2\) at the site of \(\mu_1\text{.}\)
27. Magnetization of a Copper Cylinder inside a Solenoid.
A solenoid with \(10\) turns per cm and carrying a \(0.1\, \text{A}\) current has a \(4\, \text{cm}\) long and \(1\, \text{cm}\) diameter copper cylinder inside it. Determine the magnitude and direction of magnetization of the copper cylinder?
Answer.
Magnitude \(0.97\times 10^{-3}\ \textrm{A/m}\text{,}\) Direction opposite to the magnetic field.
Solution.
First we will find the auxiliary field \(H\) from the real current in the solenoid. In the space inside the solenoid we get
\begin{equation*} H = n I = 10^{3}\times 0.1 = 100\:\textrm{A/m}, \end{equation*}
in the direction of the axis of the solenoid. The magnetization of the copper cylinder will be
\begin{equation*} M = \chi_m\:H = -0.97\times 10^{-5}\times 100\:\textrm{A/m} = -0.97\times 10^{-3} \:\textrm{A/m}. \end{equation*}
The negative sign here means that \(\vec M\) is pointed in the opposite direction to the vector \(\vec H\text{.}\)
28. Magnetic Force due to Diamagnetism of Silver.
A small piece of silver of mass \(100\, \text{mg}\) is brought close to the north pole of a magnet that has a net magnetic field \(3\, \text{T}\) and a gradient of \(20\, \text{T/m}\) at the site of the sample. Find the magnitude and direction of the force on silver piece due to its diamagnetism.
Hint.
First estimate the induced magnetic dipole moment and then calculate the force on it.
Solution.
Let there be \(N\) atoms in the sample and \(A\) the atomic number of silver. Then, the induced magnetic dipole moment will be approximately
\begin{equation*} \mu_{\textrm{ind}} = N\:A\:\dfrac{eR^2B_{\textrm{ext}}}{2\hbar}, \end{equation*}
where \(R\) is Bohr radius and \(\hbar\) is the Planck constant divided by \(2\pi\text{.}\) Now, let \(W\) be the atomic weight (in grams) of silver. Then, in \(m\) grams of silver there will be
\begin{equation*} N = \dfrac{m}{W}\times N_A, \end{equation*}
where \(N_A\) is the Avogadro number. Putting in the numbers we get
\begin{align*} \mu_{\textrm{ind}} \amp = \left( \dfrac{0.1}{108}\times 6.022\times 10^{23}\right) \\ \amp \quad\quad \times 47\times \dfrac{1.6\times 10^{-19}\times (0.53\times 10^{-10})^2\times 3}{2\times 1.055\times 10^{-34}} \times 9.27*10^{-24}, \\ \amp = 1.55 \times 10^{-6} \:\textrm{A.m}^2. \end{align*}
Multiply this with the gradient of the field to obtain the magnitude of the force on the piece of silver.
\begin{equation*} F = 1.55 \times 10^{-6} \:\textrm{A.m}^2\times 20\: \textrm{T/m} = 3.1\times 10^{-5}\:\textrm{N}. \end{equation*}
29. Nuclear Magnetic Resonance.
Nuclear magnetic resonance (NMR) uses magnetic moments of spins of nuclei. For instance consider water molecule. Its electrons all have their spins paired up as a result water is a diamagnetic material. But the protons of the two hydrogen atoms each with nuclear spin magnetic moments of magnitude \(2.79\, \mu_N\) each are free to orient in space and act as permanent dipoles. A magnetic field of \(3\, \text{T}\) is applied on a \(100\) gram water sample. (a) Find the direction and magnitude of the magnetic dipole moment due to alignment of nuclear magnetic dipoles. (b) How much energy will it take to flip \(10\%\) of the aligned dipoles by \(180^{\circ}\text{?}\)
Answer.
(a) Magnitude: \(5.89\times10^{-2} \ \textrm{A.m}^2\text{,}\) (b) \(3.53 \times 10^{-2}\ \textrm{J}\text{.}\)
Solution 1. a
First we will find the number \(N\) of hydrogen atoms in 100 g of water.
\begin{align*} N \amp = 100\:\textrm{g}\times \dfrac{6.023\times 10^{23}}{1\:\textrm{mol}}\times \dfrac{1\:\textrm{mol}}{18\:\textrm{g}}\times 2\;\textrm{H-atoms}, \\ \amp = 6.692\times 10^{24}. \end{align*}
Assuming perfect alignment of the nuclear magnetic dipoles we obtain
\begin{equation*} \mu = 6.692\times 10^{24}\times 2.79\:\mu_N = 5.89\times 10^{-2}\:\textrm{J/T}. \end{equation*}
Solution 2. b
The energy needed to flip 10\% of the dipole will be
\begin{equation*} U = 0.1\times 2\mu\: B = 0.1\times 2\times 5.89\times 10^{-2}\:\textrm{J/T}\times 3\:\textrm{T} = 3.53\times 10^{-2}\:\textrm{J}. \end{equation*}
30. Rotating Magnetic Dipoles in an External Magnetic Field.
Ten magnetic particles stick together and form a string such that the magnetization is uniform with magnitude \(8 \times 10^5 A/m\text{.}\) Each particle is cylindrically shaped with radius \(10\,\mu\text{m}\) and length \(90\, \mu\text{m}\text{.}\) If the string makes is aligned to earth’s local magnetic field of magnitude \(0.5 \times 10^{-4} \,\text{T}\text{.}\) Find energy needed to rotate the particles so that they face an angle \(30^{\circ}\) to the external field.
Hint.
Use \(U = - \vec \mu\cdot \vec B\text{.}\)
31. Magnetic Field Indside a Solenoid Filled with MAgnetic Materials.
What is the magnetic field \(\vec B\) inside a solenoid of 30 turns/cm carrying current \(2\, \text{A}\) if inside space is filled with (a) tungsten, (b) lead?
Hint.
Find \(H\) first.
32. Magnetic Field of a Bar Magnet.
A magnet shaped as a thin cylinder can be thought of as a collection of dipoles. Consider a uniformly magnetized thin bar of radius of cross-section \(a\) and length \(L\) having a uniform magnetization of magnitude \(M\) parallel to its length. Find the magnitude and direction of magnetic field at a point along the axis of the cylinder.
Answer.
Magnitude: \(\frac{\mu_0 M}{\pi}\left[\frac{1}{(2h-L)^2} -\frac{1}{(2h+L)^2}\right]\text{.}\)
Solution.
Magnetic field of an element of the magnet of size \(dz\) at \(z\) is given for the magnetic dipole moment \(Mdz\) in the element.
\begin{equation*} dB_P = \dfrac{\mu_0}{2\pi}\dfrac{Mdz}{(h-z)^3}. \end{equation*}
Now we integrate this from \(-L/2\) to \(L/2\) to obtain the net field at P.
Figure 37.30.
\begin{align*} B_P \amp = \dfrac{\mu_0\: M}{2\pi}\int_{L/2}^{L/2}\:\dfrac{dz}{(h-z)^3} = \dfrac{\mu_0\: M}{2\pi}\int_{h+L/2}^{h-L/2}\:\dfrac{dx}{x^3}, \\ \amp = \dfrac{\mu_0\: M}{\pi}\: \left[ \dfrac{1}{ (2h-L)^2} - \dfrac{1}{ (2h+L)^2} \right]. \end{align*}
33. Magnetic Field of a Thin Magnetic Disk.
A magnet shaped as a thin disk can be thought of made up of dipoles. Consider a uniformly magnetized thin disk radius \(R\) having a uniform magnetization of magnitude \(M\) perpendicular to its surface. Find (a) the magnitude and direction of the equivalent current around the rim, and (b) the magnetic field from the magnet at a point on the axis.
Answer.
(a) Magnitude: \(M\text{,}\) (b) Magnitude: \(\mu_0 MR^2/2(z^2+R^2)^{3/2}\text{.}\)
Solution 1. a
Let \(d\) be the thickness of the disk. Then, the net dipole moment of the disk will be \(\mu = \pi R^2 d M\text{.}\) Now, we can think of this as a bound current \(I\) flowing in the circle around the rim. Equating \(I\pi R^2\) to the dipole moment gives
\begin{equation*} I\pi R^2 = \mu\ \ \Longrightarrow\ \ I = M\: d. \end{equation*}
If the dipole are pointed up, then the direction of the current will be counterclockwise when seen from above.
Solution 2. b
The magnetic field of the disk will be equal to the magnetic field of the equivalent bound current found above. The field at a point \(z\) above the disk will have the magnitude
\begin{equation*} B = \dfrac{\mu_0\:IR^2}{2}\:\dfrac{1}{(R^2 + z^2)^{3/2}} = \dfrac{\mu_0\:M\;d\:R^2}{2}\:\dfrac{1}{(R^2 + z^2)^{3/2}}. \end{equation*}
The direction of the field will be pointed up if the dipoles of the disk are pointed up. If magnetization is given as per unit area rather than per unit volume, then \(Md\) in these formulas will be replaced by just \(M\text{.}\)
PrevTopNext
Found typo?