LC Circuits

Section 40.1 LC Circuits

Before we discuss a driven circuit, we will look at a simple circuit with only two elmenets and address the following question: What will happen when you connect a charged capacitor to the ends of a coil, i.e., and inductor, as in Figure 40.1? For the moment, we will ignore any resistance in the simple \(LC\)-circuit and assume an ideal condition of zero resistance.

Electrons from the negative plate of the capacitor will start to flow through the coil to the positive plate. The current starts with a maximum value and decreases to zero, but then picks up again, but this time going in the opposite direction. If we assume zero resistance, then current never dies!!

With a time-varying current in the circuit and non-zero self-inductance, a back EMF will develop in the circuit, which wil oppose the growth of current in the circuit. It turns out that the back EMF has its maximum value in this circuit precisely when capacitor has fully discharged. Now, due to the back EMF, the capacitor starts to charge again. Since current would be flowing in the reverse direction, previously negatively charged plate will become positively charged and vice-versa.

If the resistance in the circuit is negligible, very little energy can dissipate. Consequenntly, the back-and-forth charging and discharging of capacitor in the \(LC\) circuit will continue for ever. We call this phenomenon electromagnetic oscillation. This has analogy to the “perpetual motion” of a block attached to a spring with inductance serving as mass inertia and 1/capacitance serving as spring constant. Full analogy is summarized in Table 40.2.

We will prove below that current \(I(t)\) in an \(LC\)-circuit with capacitor fully charged at \(t=0\) and current value positive when flowing into positive plate and negative when flowing away from positive plate is sinusoidal.

\begin{equation} I(t) = -\omega\, Q_0\,\sin(\omega\, t),\tag{40.1} \end{equation}

where

\begin{equation} \omega = \dfrac{1}{\sqrt{LC}},\tag{40.2} \end{equation}

where \(L\) is the self-inducatance of the circuit and \(C\) capacitance in the circuit. The quantity \(\omega\) is angular frequency with which current oscillates. This frequency of an LC circuit is also called the natural frequency of the circuit. The period of oscillation is

\begin{equation} T = \dfrac{2\pi}{\omega},\tag{40.3} \end{equation}

and the cycle frequency is

\begin{equation} f = \dfrac{1}{T} = \dfrac{\omega}{2\pi}.\tag{40.4} \end{equation}

Subsection 40.1.1 (Calculus) Equation of Motion of LC circuit

We wish to determine dynamical equation for charge on one of the capacitor plates, say the upper plate in Figure 40.1. Let \(q(t)\) denote the charge on the this plate at time \(t\text{.}\) We will pick a time \(t\) when charge on the plate is positive and is building up. Then, current in the wire connected to this plate will be

\begin{equation} I(t) = \dfrac{dq}{dt}.\tag{40.5} \end{equation}

This current passes through the inductor. Therefore, the back-emf across the inductor will be

\begin{equation} \mathcal{E}_L(t) = -L \dfrac{dI}{dt}. \tag{40.6} \end{equation}

The EMF across the capacitor at this instant will be

\begin{equation} \mathcal{E}_C(t) = \dfrac{1}{C}\,q(t).\tag{40.7} \end{equation}

Now, Faraday’s loop rule around the loop of the circuit in Figure 40.1 gives the equation of motion of the charge on the upper plate.

\begin{equation} \dfrac{1}{C}\,q(t) = -L \dfrac{dI}{dt}.\tag{40.8} \end{equation}

Using Eq. (40.5) in this equation and rearranging we get the standard form of the equation of motion.

\begin{equation} \dfrac{d^2 q}{dt^2 } + \dfrac{1}{LC}\, q = 0.\tag{40.9} \end{equation}

You can immediately see analogy with the one-dimensinal simple harmonic oscillator,

\begin{equation*} \frac{d^2x}{dt^2} + \frac{k}{m}\,x = 0. \end{equation*}

Taking one more derivative of the charge equation and using Eq. (40.5), you can obtain equation of motion of current in the circuit.

\begin{equation} \dfrac{d^2 I}{dt^2 } + \dfrac{1}{LC}\, I = 0.\tag{40.10} \end{equation}

Subsubsection 40.1.1.1 Solution of Equation of Motion

General solution of equation of motion for \(q\text{,}\) Eq. (40.9) is a linear combination of sine and cosine functions of \(t\) as we have seen in our studies on simple harmonic motion.

\begin{equation} q(t) = A\,\cos(\omega\,t) + B\,\sin(\omega\,t),\tag{40.11} \end{equation}

where

\begin{equation*} \omega = \dfrac{1}{\sqrt{LC}}, \end{equation*}

and \(A\) and \(B\) are constants. You can easily verify that this is a solution of Eq. (40.10) by plugging this solution into the equation of motion. The constants \(A\) and \(B\) depend on initital state of the circuit, i.e., given charge on the capacitor and current in the circuit. For example, if at \(t=0\text{,}\) capacitor plates had charge \(\pm Q_0\) and there was no current in the circuit, \(I=0\text{,}\) then, you would have the following two equations satisfied by \(A\) and \(B\text{.}\)

\begin{align*} \amp Q_0 = A \\ \amp I = \frac{dq}{dt}\quad\rightarrow\quad (t=0)\quad \rightarrow \quad\omega\,B = 0. \end{align*}

Hence, in this case, we will have \(A=Q_0\) and \(B=0\text{.}\) Therefore,

\begin{equation} q(t) = Q_0\,\cos(\omega\,t).\tag{40.12} \end{equation}

Its derivative gives the current as a function of time.

\begin{equation} I(t) = -\omega\,Q_0\,\sin(\omega\,t).\tag{40.13} \end{equation}

Subsection 40.1.2 Analogy Between Simple Harmonic Oscillator and LC Circuit

Note that Eq. (40.9) is same as equation of a block attached to spring, the simple harmonic oscillator. Therefore, there is an important analogy between the mechanical system and corresponding electric circuit. Table 40.2 displays this analogy.

Table 40.2. Analogy Between Harmonic Oscillator and Oscillating Circuit


Mechanical System	Electrical System
Mass (\(m\))	Inductance (\(L\))
Spring constant (\(k\))	Inverse capacitance \(\left(\dfrac{1}{C}\right)\)
Damping constant (\(b\))	Resistance (\(R\))
Position (\(x\))	Charge (\(q\))
Velocity (\(v\))	Current (\(I\))
Kinetic energy, \(\dfrac{1}{2}mv^2\)	Magnetic energy, \(\dfrac{1}{2}LI^2\)
Potential energy, \(\dfrac{1}{2}kx^2\)	Electrical energy, \(\dfrac{1}{2}\dfrac{1}{C}q^2 =\dfrac{1}{2}CV_C^2\)

Subsection 40.1.3 Energy in an LC-Circuit

The analogy between the electrical and mechanical systems also extends to the energy in the circuit with the magnetic field energy being analogous to the kinetic energy and the electric field energy to the potential energy. With \(I\) current in the circuit and \(V_C\) voltage across the capacitor, the net constant in the circuit will be

\begin{equation} U_\text{net} = \frac{1}{2}LI^2 + \frac{1}{2}CV_C^2.\tag{40.14} \end{equation}

In the absence of resistance in the circuit, this energy is conserved over time. Thus, if the circuit in Figure 40.1 started out with voltage \(V_0\) and zero current, then at time \(t\) after closing the circuit, we expect the following from conservation of energy.

\begin{equation} \frac{1}{2}LI^2 + \frac{1}{2}CV_C^2 = \frac{1}{2}CV_0^2.\tag{40.15} \end{equation}

Let \(t=t_1\) when capacitor is discharged fully. At this instant, the voltage across the capacitor will be zero and current in the circuit will be maximum. Let \(I_\text{max}\) be current at this instant. Conservation of energy gives

\begin{equation*} \frac{1}{2}LI_\text{max}^2 = \frac{1}{2}CV_0^2. \end{equation*}

We can solve this to find an expression for maximum current in this oscillating circuit.

\begin{equation} I_\text{max} = \sqrt{C/L}\,V_0 = \omega\: C\: V_0.\tag{40.16} \end{equation}

In Figure 40.3, I have plotted the energies in the electric field and the magnetic filed for the following values of constants, \(C=\frac{1}{2}\text{ F}\text{,}\) and \(L=2\text{ H}\text{,}\) and \(V_0=1\text{ V}\text{.}\) We see that sum of the energies is constant but at sometime all of the energy is in electric field, at some other time all the energy is in the magnetic field, and the rest of the time the energy is in both fields.

Figure 40.3. The total energy in an LC circuit oscillates between completely in the electric field between the plates of the oscillator to completely in the magnetic field. The curve with a solid line is the magnetic energy and the one with dashed line the electrical energy. The horizontal line the total energy which does not change with time.

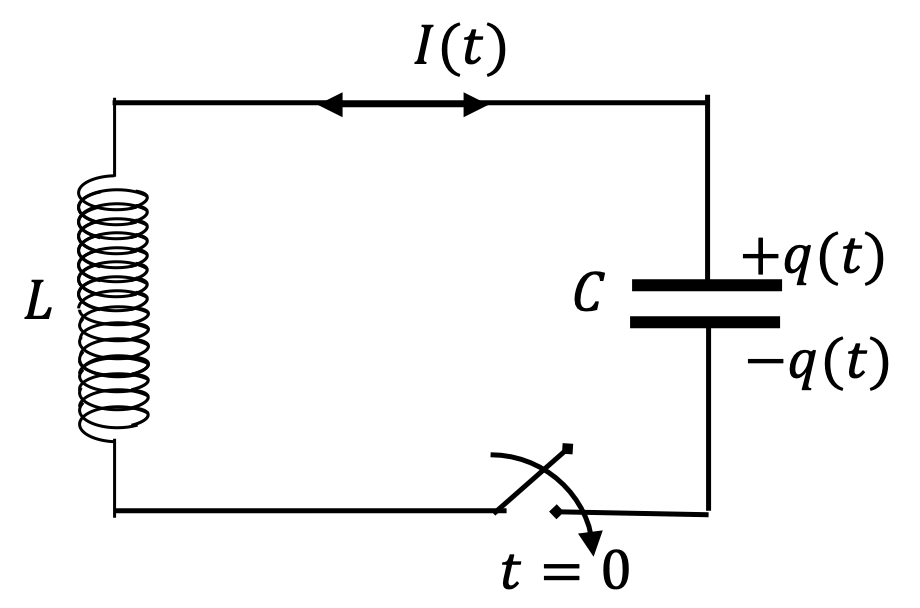
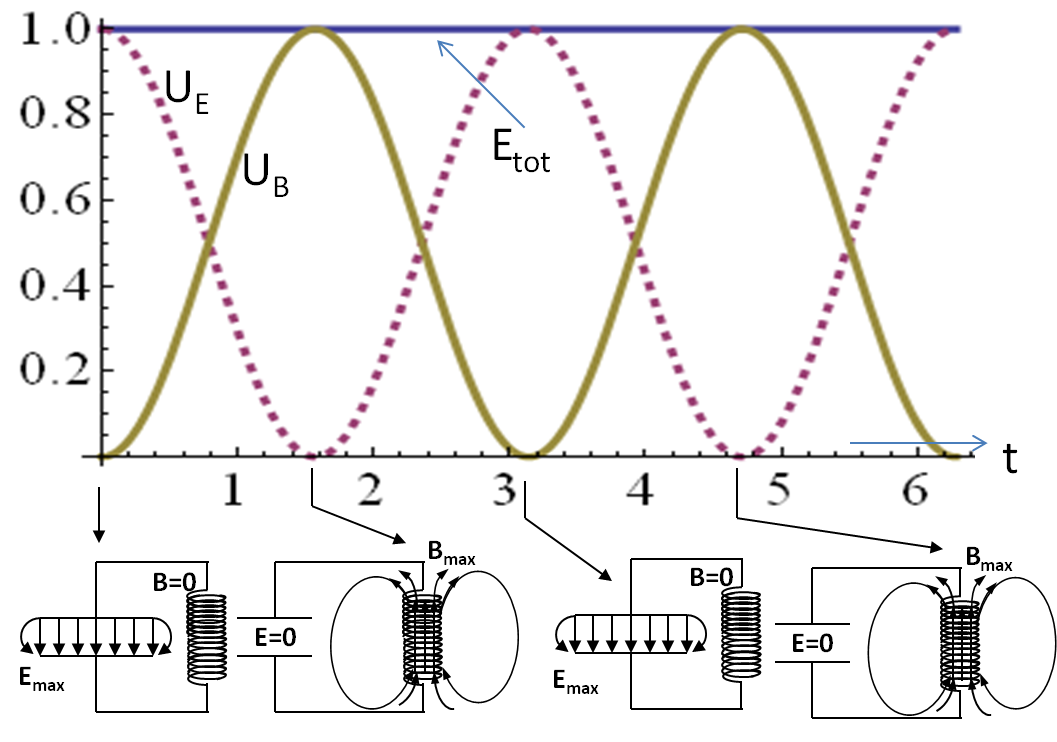
Example 40.4. Frequency of Oscillations of an LC-circuit and Voltage at an Instant.

A \(3\text{-F}\) capacitor is charged so that it contains \(\pm30\,\mu\text{C}\) on its plates. It is then connected in series to a \(2\text{-H}\) inductor through a switch. The switch is closed at \(t = 0\text{.}\)

(a) Find the frequency of oscillations of the circuit.

(b) Find the voltage across the capacitor at \(t = 0.3\text{ sec}\text{.}\)

Answer.

(a) \(6.5\times 10^{-2}\ \text{Hz}\text{,}\) (b) \(9.9\ \text{V}\text{.}\)

Solution 1. (a)

The frequency \(f\) is related to the angular frequency \(\omega\) by \(2\pi f = \omega\text{.}\) Therefore,

\begin{equation*} f= \frac{1}{2\pi\sqrt{LC}} = 6.5\times 10^{-2}\ \text{Hz}. \end{equation*}

Solution 2. (b)

The initial voltage will be related to the initial charge by \(V_0 = Q_0/C = 10\,\text{ V}\text{.}\) Therefore, the voltage at \(0.3\text{ sec}\) will be

\begin{equation*} V(0.3\ \text{sec}) = (10\ \text{V})\ \cos(2\ \pi\times 0.065\ \text{Hz}\times\ 0.3\ \text{sec}) = 9.9\ \text{V}. \end{equation*}

Example 40.5. Inductance, Energy, and Current of an LC circuit from Period of Oscillations.

A \(40\text{-}\mu\text{F}\) capacitor is connected across a \(10\text{-V}\) battery till it is fully charged. It is then disconnected and connected across an inductor. The current in the \(LC\) circuit so formed oscillated with a period of \(5\text{ msec}\text{.}\)

Determine (a) the inductance of the inductor, (b) the total energy of the circuit, and (c) the maximum current in the circuit.

(d) If at some instant, current in the circuit is half of the maximum, what is the amount of charge at that instant on the plate of the capacitor whose charging corresponds to postitive current flowing into that plate?

Answer.

(a) \(0.016\ \text{H} \text{,}\) (b) \(2\ \text{mJ}\text{,}\) (c) \(0.5\text{ A}\text{,}\) (d) \(35\ \mu\text{C}\text{.}\)

Solution 1. (a)

From \(\omega = 1/\sqrt{LC}\) we obtain the following for \(L\) in terms of the period \(T\) of the oscillations.

\begin{align*} L \amp = \frac{1}{\omega^2 C}= \frac{T^2}{4\pi^2 C} \\ \amp = \frac{(0.005\ \text{s})^2}{4\pi^2 \times 40\times 10^{-6}\text{F}} = 0.016\ \text{H}. \end{align*}

Solution 2. (b)

The total energy in the circuit will be equal to the energy at any time, say at \(t=0\text{,}\) which is

\begin{align*} E(t=0) \amp = \frac{1}{2}CV_0^2\\ \amp = \frac{1}{2}\times 40\times 10^{-6}\text{F} \times (10\ \text{V})^2 = 2\ \text{mJ}. \end{align*}

Solution 3. (c)

Use conservation of energy to figure out the maximum current in the circuit. That will happen when all the energy is in the magnetic field.

\begin{equation*} \frac{1}{2}LI_{\text{max}}^2 = 2\ \text{mJ} \end{equation*}

This gives \(I_{\text{max}} = 0.5\text{ A}\text{.}\)

Solution 4. (d)

(d) Use conservation of energy for arbitrary time. Writing the energy in the capacitor in terms of the charge on the capacitor instead of the voltage across the capacitor we have

\begin{equation*} \frac{1}{2}LI(t)^2 + \frac{1}{2C}q(t)^2 = 2\ \text{mJ}\equiv E_{\text{tot}}. \end{equation*}

Since current at this time is given to be \(I = 0.25\, \text{A}\text{,}\) we can find \(q\) at that instant.

\begin{equation*} q = \sqrt{2 C E_{\text{tot}} - I^2/\omega^2 } = 35\ \mu\text{C}. \end{equation*}

Example 40.6. Natural Frequency of LC Circuits.

Find natural frequencies of circuits in Figure 40.7.

Answer.

(a) \(503\text{ Hz}\text{,}\) (b) \(0.503\text{ Hz}\text{,}\) (c) \(356\text{ Hz}\text{,}\) (d) \(712\text{ Hz}\text{.}\)

Solution.

For (c) the net capacitance is sum \(C = C_1 + C_2\) since the capacitors are in series. In (d), the net capacitance is obtained by adding them in inerse, \(\dfrac{1}{C} = \dfrac{1}{C_1} + \dfrac{1}{C_2} \text{.}\)

The angular frequencies are

\begin{align*} \amp\text{(a) } \omega_a = \dfrac{1}{\sqrt{LC}} = 3162.3\text{ sec}^{-1}. \\ \amp\text{(b) } \omega_b = \dfrac{1}{\sqrt{LC}} = 3.162\text{ sec}^{-1}. \\ \amp\text{(b) } \omega_c = \dfrac{1}{\sqrt{LC}} = 2236\text{ sec}^{-1}. \\ \amp\text{(b) } \omega_d = \dfrac{1}{\sqrt{LC}} = 4472\text{ sec}^{-1}. \end{align*}

As regular frequencies, we have \(f= \omega/2\pi\text{.}\)

\begin{align*} \amp\text{(a) } f_a = 503\text{ Hz}. \\ \amp\text{(b) } f_b = 0.503\text{ Hz}. \\ \amp\text{(b) } f_c = 356\text{ Hz}. \\ \amp\text{(b) } f_d = 712\text{ Hz}. \end{align*}

Example 40.8. Mechanical Equivalents of Electrical Circuits.

For each of the circuits in Example 40.6 draw the equivalent mechanical circuit.

Solution 1. a

The mechanical equivalent of this circuit will oscillate undamped at the same frequency as the electrical circuit.

This can be given by a mass \(m\) attached to a spring of spring constant \(k\) as shown. The values of \(m\) and \(k\) should be such that \(\sqrt{k/m} = 3.16\times 10^{3}\:\textrm{sec}^{-1}\text{.}\) You could take \(m= 1\:\textrm{kg}\) and \(k = 9.99\times 10^{6}\:\textrm{N/m}\text{.}\)

Solution 2. b

The mechanical equivalent of circuit (b) is similar to part (a).

Solution 3. c

The mechanical equivalent of the circuit with parallel capacitors corresponds to springs in series since \(1/C\) corresponds to \(k\) in the fundamental frequency formula \(1\sqrt{LC}\) in electrical circuit corresponding to \(\sqrt{k/m}\) in the mechanical analogue with \(L\) acting as inertia \(m\text{.}\)

Solution 4. d

The mechanical equivalent of the circuit with series capacitors corresponds to springs in parallel.

Prev Top Next