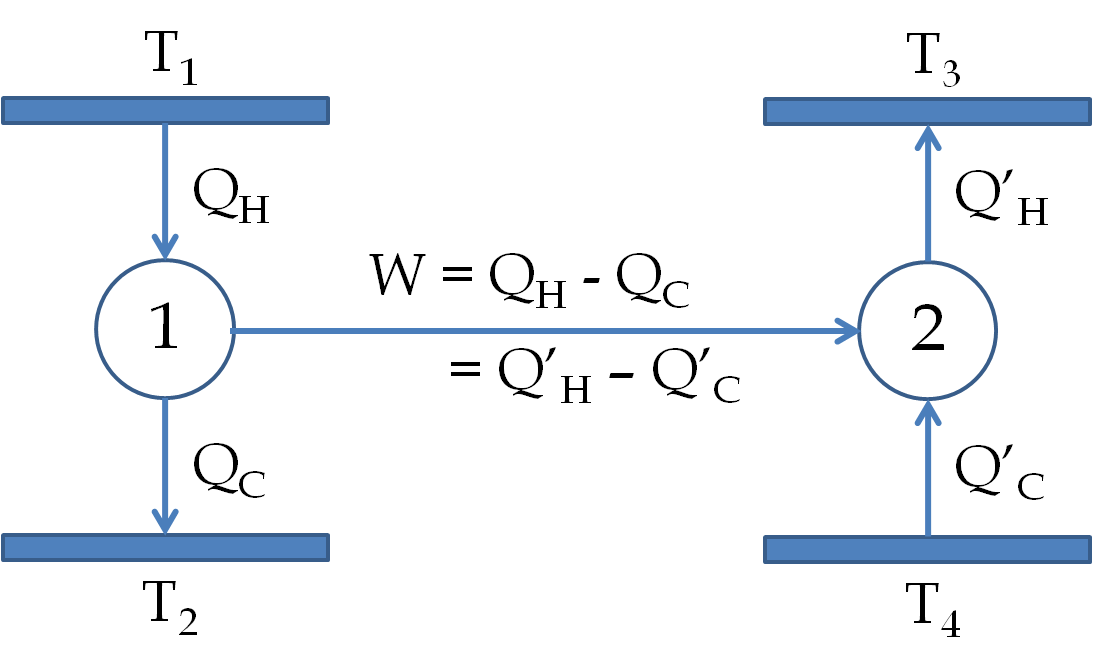
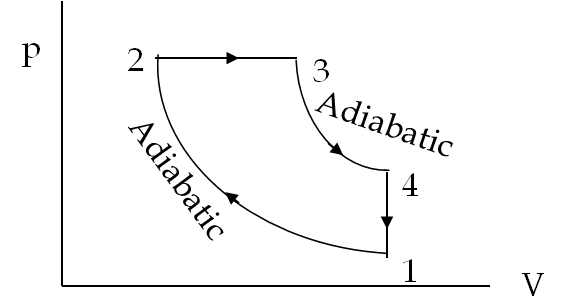
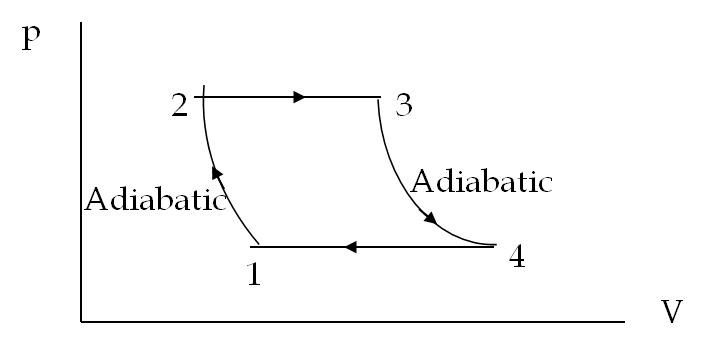
The calculations for the work in the steps in this cycle are similar to the ones presented in the last problem. We can write the answer by inspection.
\begin{align*}
\amp W_{12} = \frac{3}{2}\left(p_1V_1 - p_2V_2 \right)\\
\amp W_{23} = p_3 V_3 - p_2V_2 \\
\amp W_{34} = \frac{3}{2}\left(p_3V_3 - p_4V_4 \right) \\
\amp W_{41} = p_1 V_1 - p_4V_4
\end{align*}
Therefore, work done by the working substance in a cycle will be
\begin{equation*}
W = \frac{5}{2} \left( p_1V_1 + p_3 V_3- p_2V_2 - p_4V_4 \right).
\end{equation*}
The heat input occurs in the 2-3 step of the cycle. Using the first law for this step we obtain
\begin{equation*}
Q_{in} = U_{23} + W_{23} = \frac{5}{2}\left(p_3V_3 - p_2V_2 \right).
\end{equation*}
\begin{equation}
\eta = \frac{W }{Q_{in}} = 1 - \frac{ p_4V_4 - p_1V_1 }{ p_3V_3 - p_2V_2 }.\tag{25.15}
\end{equation}
Various pressures and volumes in this equation are related by the processes.
\begin{align*}
\amp p_2 = p_3 \\
\amp p_1 = p_4 \\
\amp p_1 V_1^{\gamma} = p_2 V_2^{\gamma} \\
\amp p_2 V_3^{\gamma} = p_1 V_4^{\gamma}
\end{align*}
These relations give
\begin{equation*}
\frac{V_4}{V_1} = \frac{V_3}{V_2} \ \ \textrm{and}\ \ \frac{V_1}{V_2} = \left( \frac{p_2}{p_1} \right)^{1/\gamma}.
\end{equation*}
We can use these relations in Eq.
(25.14) to obtain
\begin{equation*}
\eta = 1 - \left( \frac{p_1}{p_2} \right)^{(\gamma-1)/\gamma}
\end{equation*}