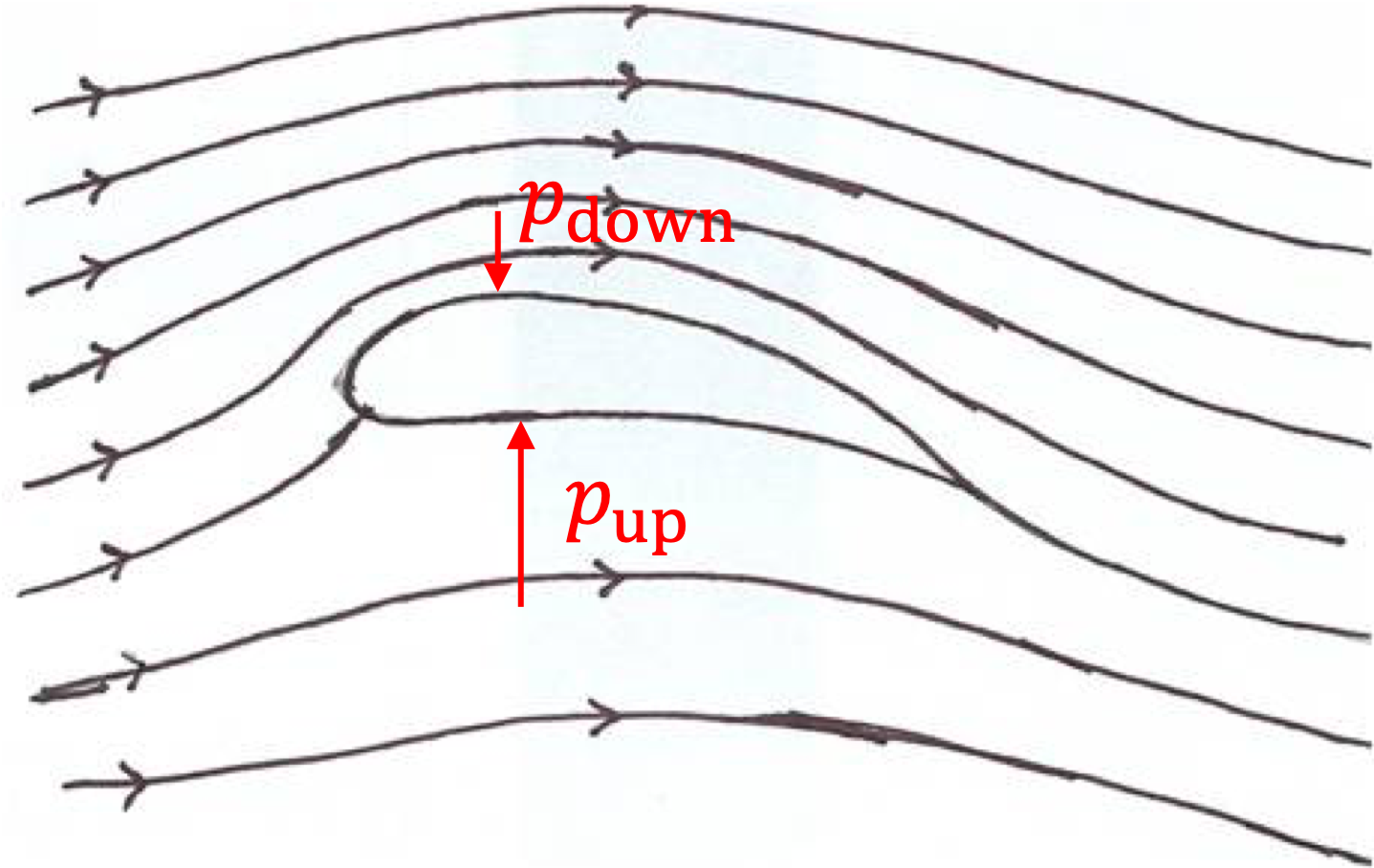
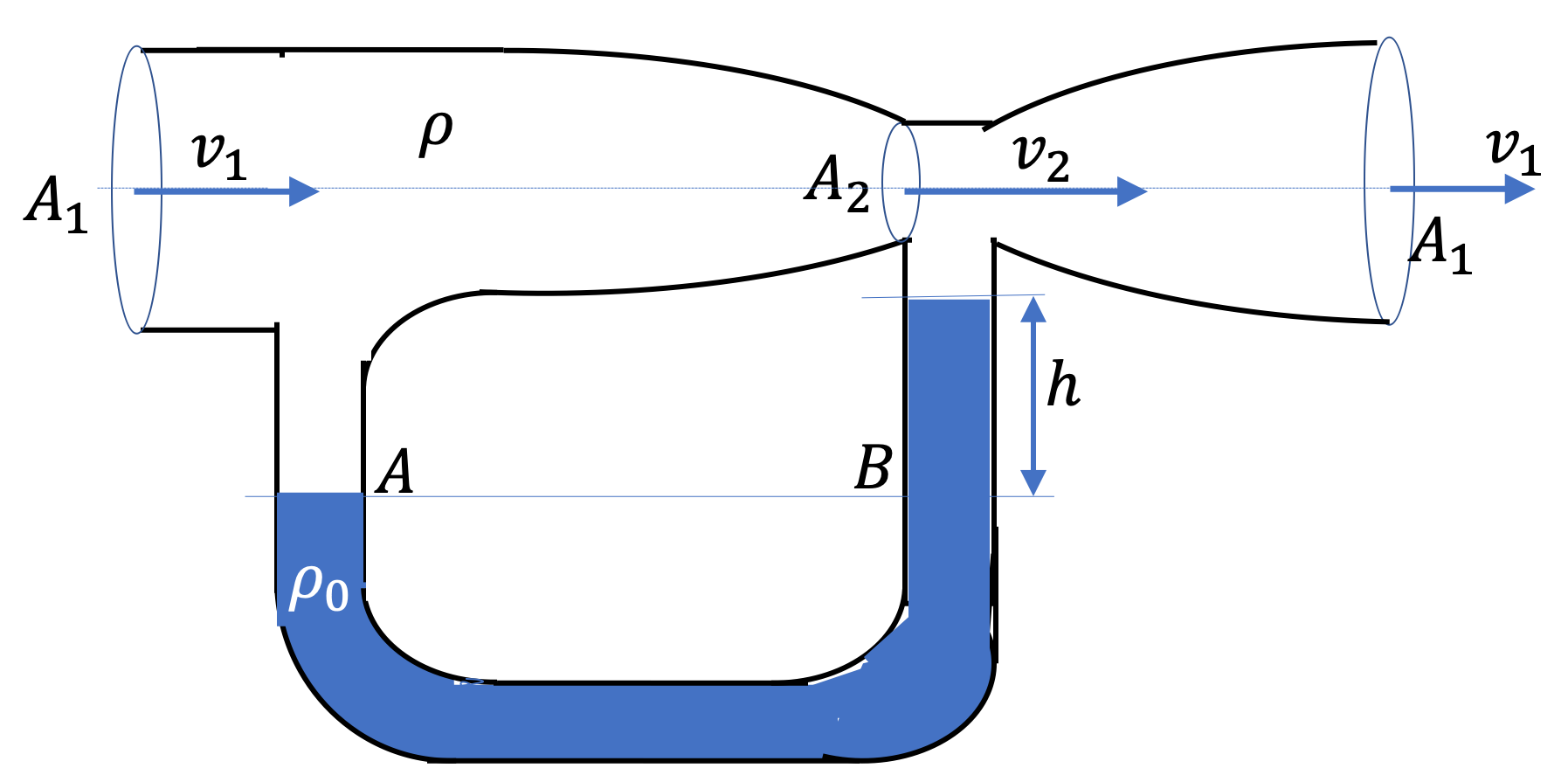
Let \(p_1\) be the pressure at the inlet and \(p_2\) at the constricted point shown in the figure. Applying Bernoulli’s equation to the flowing fluid of density \(\rho\) at the inlet and outlet at the same height we obtain the following equation.
\begin{equation}
p_1 + \frac{1}{2}\rho v_1^2 = p_2 + \frac{1}{2}\rho v_2^2.\tag{18.21}
\end{equation}
Another relation between the pressures at the inlet and outlet is obtained by applying the static pressure condition on the fluid of density \(\rho_0\) in the tube. Let \(H\) be the height of flowing fluid above A. Then, we have \(H-h\) the height of flowing fluid in the right side of the U tube. Equating the fluid pressure at A with that at B we get
\begin{equation}
p_1 \rho g H = p_2+ \rho g (H-h) + \rho_0 g h.\tag{18.22}
\end{equation}
\begin{equation}
\left( \rho_0-\rho \right) gh = \frac{1}{2}\rho v_2^2- \frac{1}{2}\rho v_1^2. \tag{18.23}
\end{equation}
The equation of continuity for flowing gas between the inlet and outlet gives us the other relation we need to find \(v_1\text{.}\)
\begin{equation}
A_1v_1 = A_2 v_2.\tag{18.24}
\end{equation}
Eliminating
\(v_2\) from Eqs.
(18.23) and
(18.24), we find the following result for the speed of gas at the inlet.
\begin{equation}
v_1 = A_1\sqrt{\frac{2(\rho_0-\rho)gh}{\rho\left( A_1^2-A_2^2 \right)}}. \label{}\tag{18.25}
\end{equation}
Therefore, we can write \(v_1\) in a more compact way
\begin{equation}
v_1 = \alpha\,\sqrt{ h },\tag{18.26}
\end{equation}
where
\(\alpha\) is a constant. Recording the difference in the two arms of the U-tube for the static fluid of density
\(\rho_0\) gives us
\(h\) which lets us determine the flow speed of the flowing fluid of density
\(\rho\) at the inlet by Eq.
(18.25).
The formula in Eq \ref{eq:venturi-eqn} can be simplified by introducing the following ratios.
\begin{align*}
\amp x \equiv \frac{\rho_0}{\rho},\\
\amp y \equiv \frac{A_2}{A_1}.
\end{align*}
With these changes Eq
(18.25) becomes
\begin{equation}
v_1 = \sqrt{\frac{2(x-1)gh}{\left( 1-y^2 \right)}}, \tag{18.27}
\end{equation}
which has the added advantage that we do not need to worry about the particular system of units for the densities and the areas because they cancel out in the ratios.