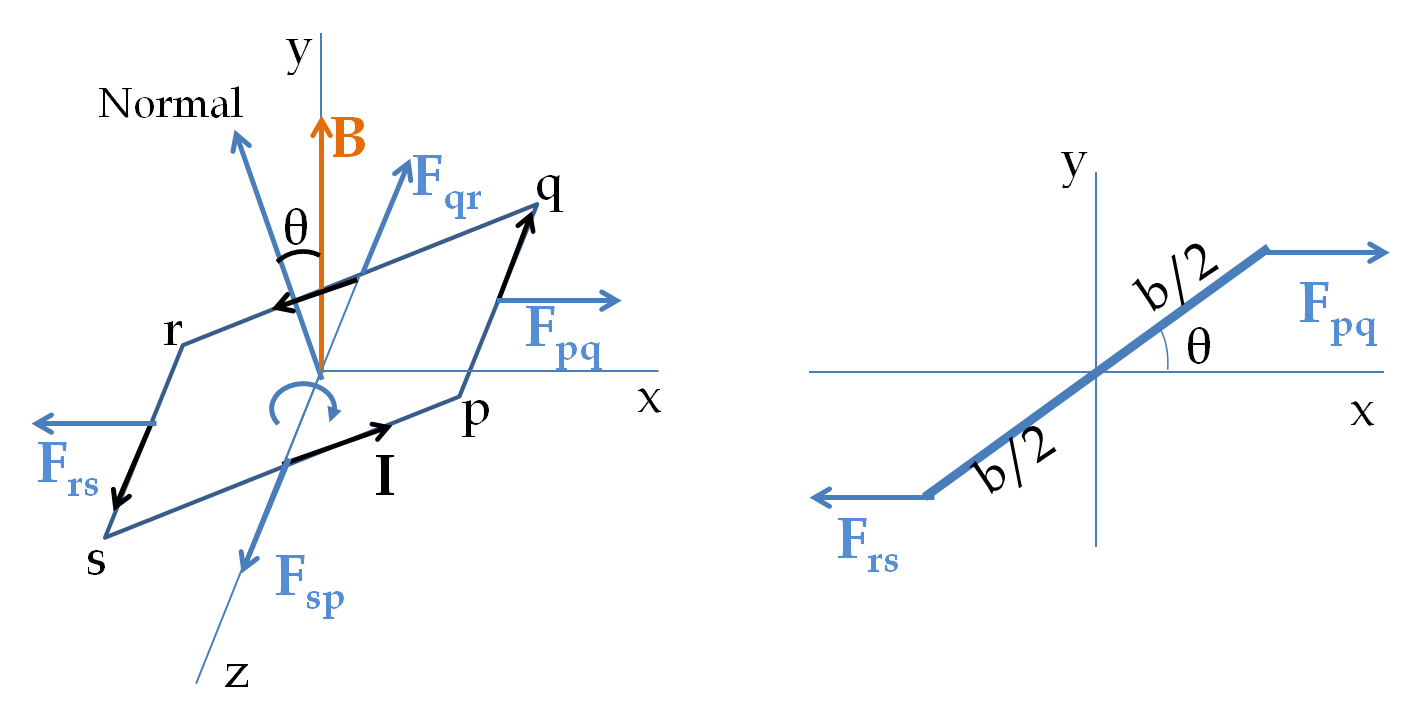
Consider a rectangular loop of current in a uniform magnetic field as shown in
Figure 35.41. For future use, I have chosen normal direction by using a right-hand rule to sweep around the loop in the direction of the current and thumb giving the direction of normal. We will examine the torque at an instant when the normal to the loop makes an angle
\(\theta\) with respect to the magnetic field. Let the loop be pivoted about an axis perpendicular to the magnetic field and passing through the middle of two of the sides of the loop as shown in
Figure 35.41
The mangentic forces on segments qr and ps are parallel to the
\(z\) axis and will not have any torque about the
\(z\) axis. Therefore, we only need torques by forces
\(\vec F_{pq}\) and
\(\vec F_{rs}\) on pq and rs respectively. The magnitudes of these toques about the
\(z\) axis are equal and have the same sense of rotation, which can be seen to be clockwise sense in right side of
Figure 35.41.
Therefore, it is sufficient to figure out torque by \(\vec F_{pq}\) only and multiply the result by 2. Using the magnetic force on the current in the pq segment we find the force to be
\begin{equation*}
\vec F_{pq} = -I a \hat k \times B \hat j = Ia B \hat i,
\end{equation*}
where
\(a\) is the length of the pq segment and I used the unit vectors along the Cartesian axes. To get a better feel of the direction of the forces, right side of
Figure 35.41 shows the forces in the
\(xy\)-plane. The lever arm of this force is
\begin{equation*}
l_\perp = \dfrac{b}{2}\,\sin\,\theta.
\end{equation*}
Therefore, the torque has magnitude
\begin{equation*}
\tau_{pq} = I a B \dfrac{b}{2}\,\sin\,\theta,
\end{equation*}
with clockwise sense of rotation. Multiplying this by 2 we get the net torque to be
\begin{equation*}
\tau_\text{net} = I a b B \sin\,\theta
\end{equation*}
Notice that \(a\times b\) is area \(A\) of the loop. Therefore, we can write this result in another form.
\begin{equation}
\tau_\text{net} = I A B \sin\,\theta\tag{35.24}
\end{equation}