Pressure Measurements

Section 17.4 Pressure Measurements

The variation of pressure with height provides a simple way to measure pressure. This principle was utilized in the invention of mercury barometer by the Italian mathematician and physicist Evangelista Torricelli (1608-1647) in 1643. Since then, many other techniques of pressure measurement have been developed.

Any property that changes with pressure in a known way can be used to construct pressure-measuring devices called pressure gauges.

The most common ones are the strain gauges, which use the change in shape of a material with pressure. The change in shape can be amplified mechanically or electrically. The tire pressure gauge shown in the image uses a mechanical way to diaplay the pressure. (Image Credit: “By JEG14 - Own work, Public Domain, https://commons.wikimedia.org/w/index.php?curid=52069008”. )

The electrically detected pressure gauges use various electrical properties that depend on material between two poles. For instance, resistance gauges uses resistance of a wire which changes due to the change in length and thickness of specially made wire mesh. The capacitance pressure gauges use the change in capacitance due to shape change with pressure.

Figure 17.9. Picture of an unmounted resistance pressure gauge. Once mounted, pressure from the horizontal direction will shrink the length and increase the thickness of the wires, thus reducing the resistance, which can be detected by appropriate electrical circuit. Credits: https://upload.wikimedia.org/wikipedia/commons/0/0a/Unmounted_strain_gauge.jpg.

The piezoelectric pressure gauge which generates a voltage difference across a piezoelectric material under pressure difference between the two sides, and the ion gauges which measures pressure by ionizing molecules in highly evacuated chambers and measuring conductivity of the ionized gas. Different pressure gauges are useful in different pressure ranges and under different physical situations.

Gauge Pressure:

Pressure gauges often measure the difference of the absolute pressure and the ambient pressure and hence the name gauge pressure. Open manometer, decribed below in Subsection 17.4.3, is one kind of pressure gauge. Tire pressure gauge measures the pressure difference between the air inside the tire and the atmospheric pressure. Therefore, the actual pressure or the absolute pressure in the tire is gauge reading plus atmospheric pressure.

Subsection 17.4.1 Mercury Barometer

Evangelista Torricelli (1608-1647) invented mercury barometer in 1643. A mercury barometer is a tube with an opening at one end and closed at the other. The tube is wide enough that fluid can flow freely in the tube. The tube is filled with mercury and the open end covered so that no air is trapped in the tube when the tube is inverted. The filled tube is then inverted and opened in a mercury tank such that no air can enter the tube.

At the neck, marked X in the tube, the upward force by pressure transmitted by the atmospheric pressure at the open surface at that level of mercury balances the weight of mercury above in the tube, \(p_0 A = (Ah\rho) g\) \(\longrightarrow\) \(p_0 = \rho g h\text{.}\) To balance atmospheric pressure, the height \(h \approx 29.9\text{ inches}\text{.}\) With density of mercury \(13600\text{ kg/m}^3\text{,}\) \(p_0 = 101324\text{ Pa}\text{.}\)

Subsection 17.4.2 Closed-tube Manometer

The pressure of a gas can be measured by making a modification to the barometer. The inverted tube of Torricelli’s experiment is made into a U-shaped tube with the open end, rather being exposed to the atmosphere, is connected to the gas container whose pressure we wish to measure as in Figure 17.11. The instrument is called a manometer.

Figure 17.11. A closed-tube manometer to measure gas pressure. The gas pressure pushes on the liquid. With vacuum on the closed end, the difference in the levels on the two sides is a measure of gas pressure, \(p = \rho g h \text{,}\) as shown in text below.

Balancing forces at a particle at the gas pressure level gives

\begin{equation*} pA = \rho A h g, \end{equation*}

where \(p\) is the gas pressure, \(\rho\) the density of the liquid in the tube, \(h\) the height above the gas pressure level, and \(A \) the area of cross-section of the closed end tube. Simplifying the equation we find the following for the pressure reading for the gas.

\begin{equation*} p = \rho g h. \end{equation*}

The closed end of a manometer are calibrated and marked for directly reading off the pressure.

Subsection 17.4.3 Open-end Manometer

Manometers can also be constructed to read the difference of pressure of the gas and the atmospheric pressure, called the gauge pressure, if both ends of the U-tube are open as I will show now. One end of the U-tube is opened to air and the other to the gas as shown in Figure 17.12.

Figure 17.12. A open-tube manometer to measure gas pressure. The gas pressure pushes on the liquid from one side and air pushes from the other side. The difference in the levels on the two sides is a measure of gas pressure minus the atmospheric pressure, \(p = p_0 + \rho g h \text{,}\) as shown in text below.

Balancing forces at a particle at the gas pressure level gives

\begin{equation*} pA = p_0 A + \rho A h g, \end{equation*}

where \(p\) is the gas pressure, \(p_0\) the atmospheric pressure, \(\rho\) the density of the liquid in the tube, \(h\) the height above the gas pressure level, and \(A \) the area of cross-section of the closed end tube. Simplifying the equation we find the following for the pressure reading for the gas.

\begin{equation*} p = p_0 + \rho g h. \end{equation*}

The difference \(p - p_0\) is called the gauge pressure.

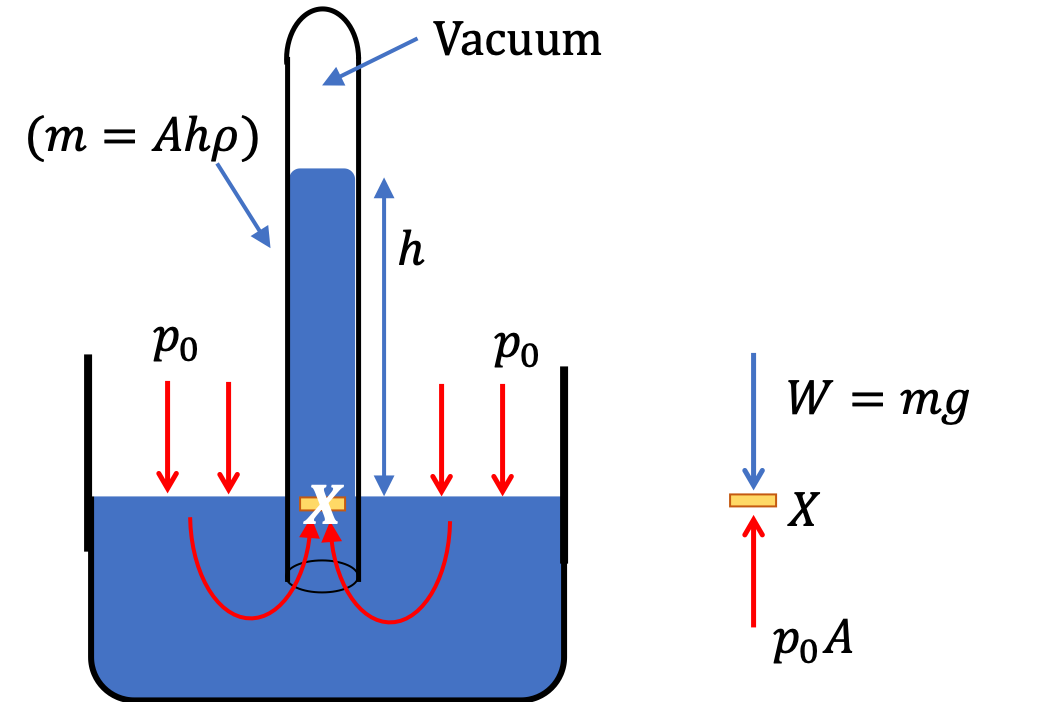
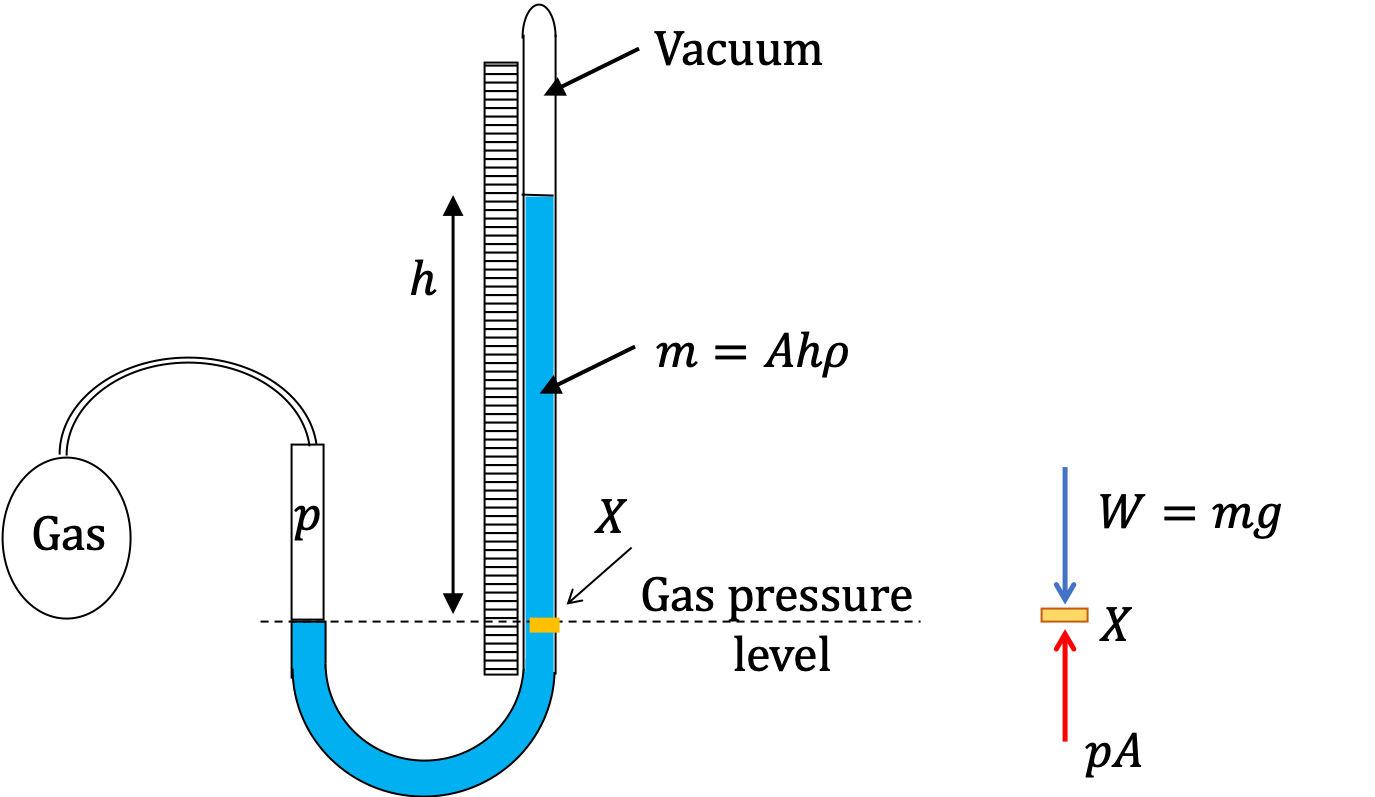
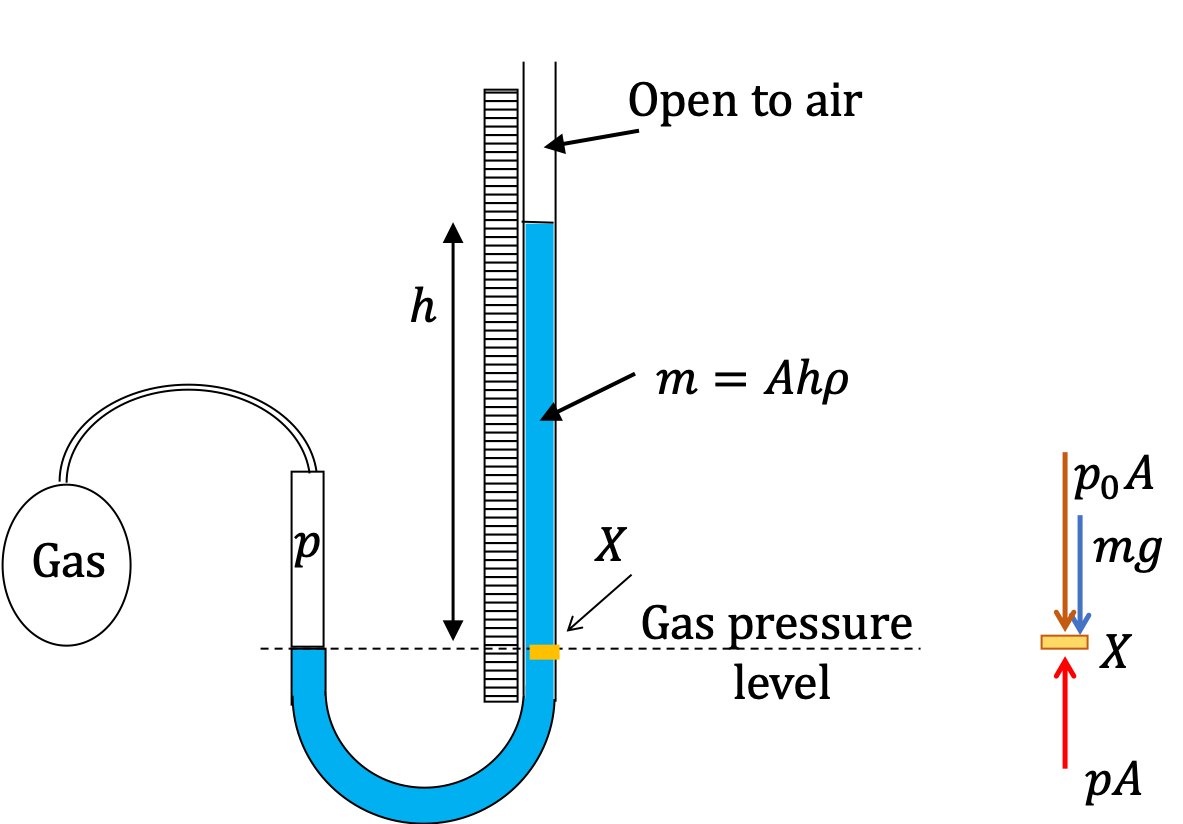
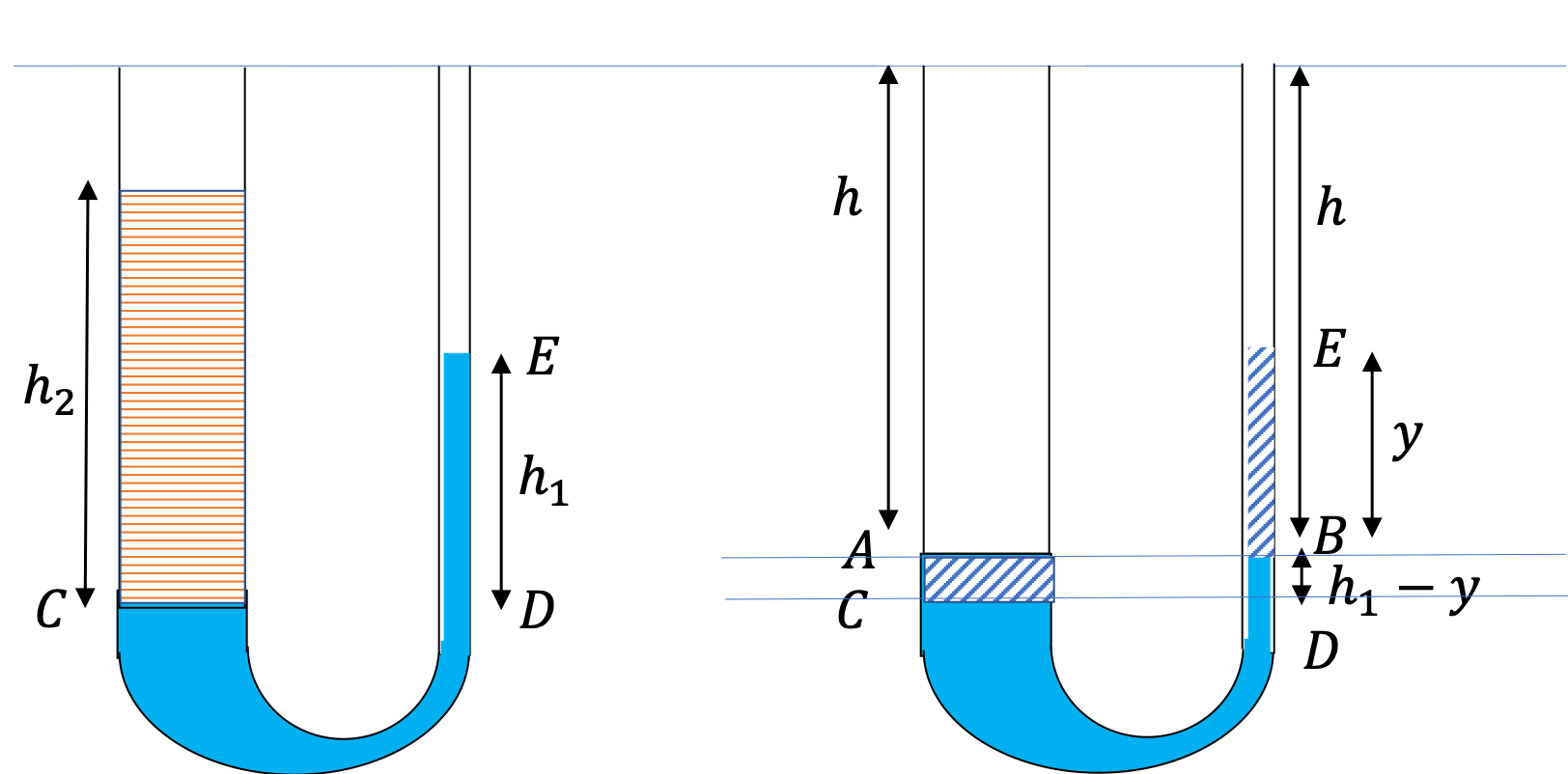
Example 17.13. Fluid Heights in an Open U-tube.

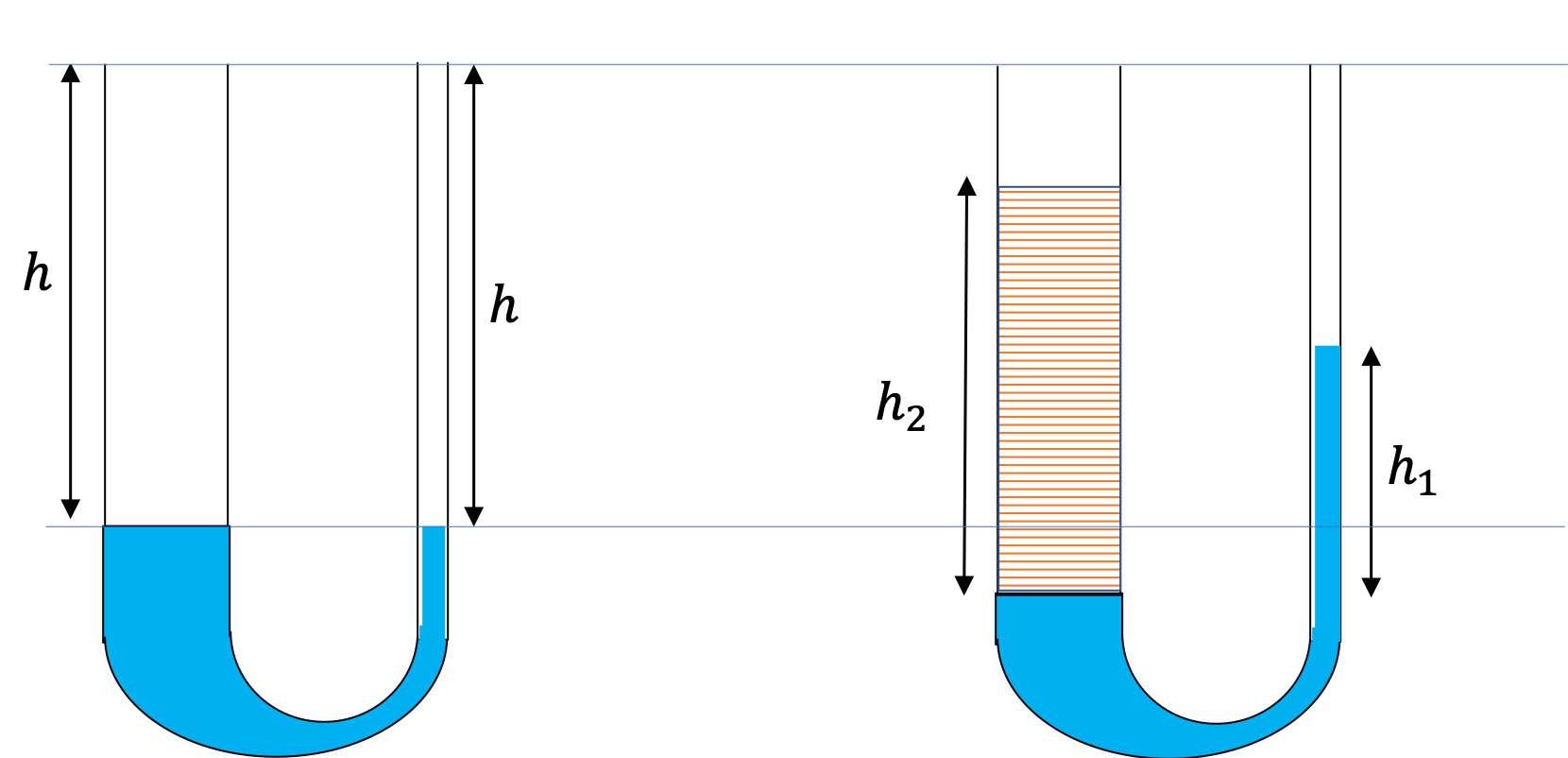
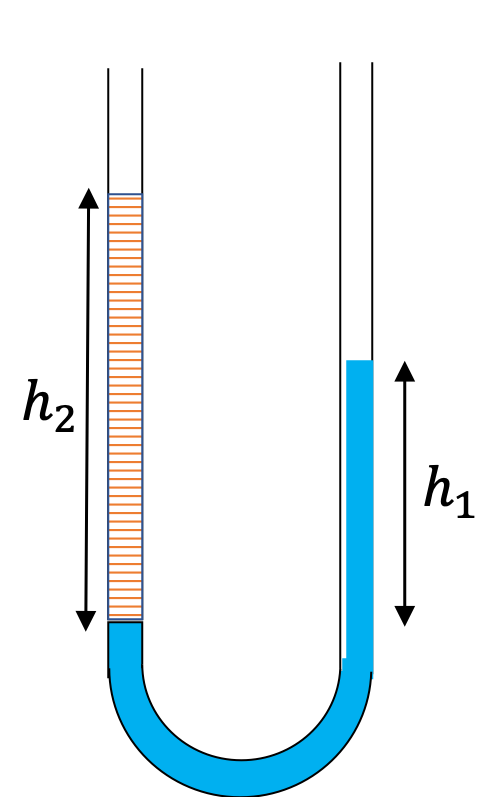
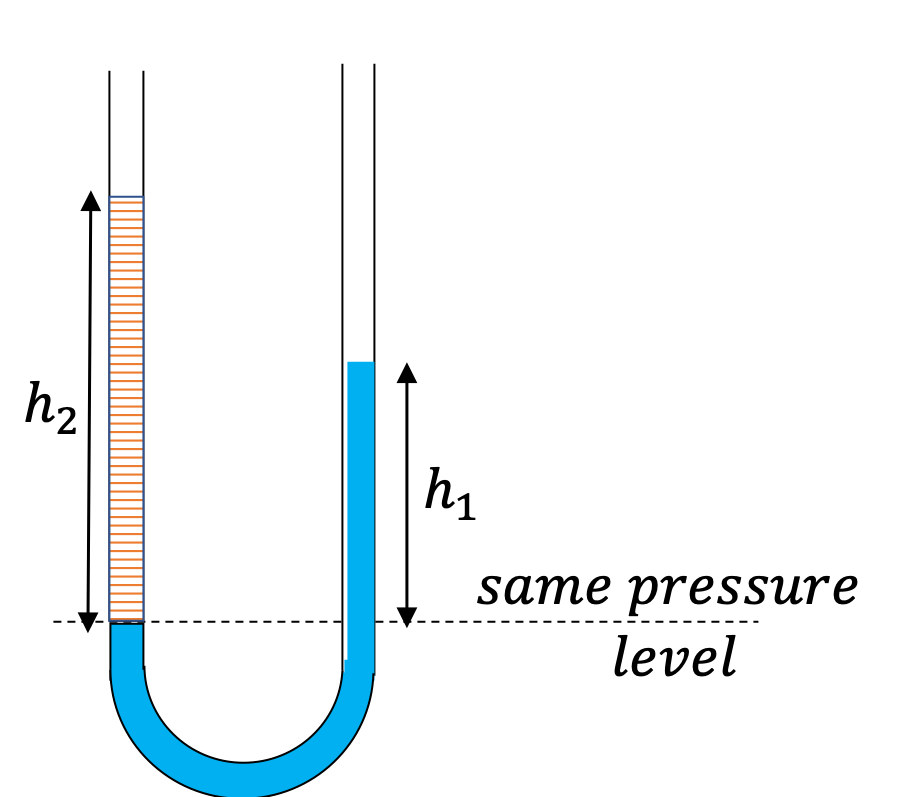
A U-tube with both ends open is filled with a liquid of density \(\rho_1\) to a height \(h \) on both sides. A liquid of density \(\rho_2\lt \rho_1\) is poured on one side. We find that liquid 2 settles on top of liquid 1, with the heights on the two sides now becoming different. The height to the top of the liquid 2 from the interface of the two liquids is \(h_2\) and the height to the top of liquid from the level of the interface is \(h_1\text{.}\) Find \(h_2 - h_1 \text{.}\)

Answer.

\(\left( 1- \frac{\rho_1}{\rho_2} \right) h_2\text{.}\)

Solution.

The pressure at the same height on the two sides of a U-tube must be same as long as the two points are connected by a continuous line in the same liquid. Therefore, we consider two points at the same level in the two arms of the tube: One point will be the interface on the side of the liquid 2 and the other will be a point in the arm with liquid 1 that is at the same level as the interface in the other arm.

\begin{align*} \amp \text{Pressure on the side with liquid 1} = p_0+\rho_1 g h_1. \\ \amp \text{Pressure on the side with liquid 2} = p_0+\rho_2 g h_2. \end{align*}

Since, the two points are in liquids 1, one at the top of the left side of liquid 1 and the other in the liquid on the right side at the same height, the pressure at the two points must be the same pressure. Therefore, we have

\begin{equation*} p_0+\rho_1 g h_1 = p_0+\rho_2 g h_2. \end{equation*}

Hence,

\begin{equation*} \rho_1 h_1 = \rho_2 h_2. \end{equation*}

This says that the difference in heights of the two sides on the U-tube would be

\begin{equation*} h_2-h_1 = \left( 1- \frac{\rho_1}{\rho_2} \right) h_2. \end{equation*}

The result makes sense if we set \(\rho_2=\rho_1\text{,}\) which gives \(h_2=h_1\text{.}\) If the two sides have the same density, they would have the same height.

Exercises 17.4.4 Exercises

1. A U Tube of Different Cross Sections and Different Liquids.

An open U-tube has different cross-sections on the two sides as shown in Figure 17.16. On one side the cross-section is \(2.5\text{ cm}^2\) and on the other side it \(4.0\text{ cm}^2\text{.}\) Water is poured so that the level is \(30\text{ cm}\) from the top on both sides.

Find the volume of the oil of density \(0.8\text{ g/cm}^3\) that must be poured on the wider end so that water rises by \(2\text{ cm}\) on the other end, i.e., the level now would be \(28\text{ cm}\) from the top on that end.

Figure 17.16. Figure for Exercise 17.4.4.1.

Hint.

Water displaced from the wider side ends up on top of the original level in the narrow side.

Answer.

\(6.16\text{ cm}^3\text{.}\)

Solution.

We will use Figure 17.17 to answer this question.

Balancing the pressure at point C, by force from above by liquid 2 and by force from below from pressure in liquid 1 at this level, we will get

\begin{equation} \rho_1 h_1 = \rho_2 h_2.\tag{17.12} \end{equation}

Now, we note from the displacement of liquid 1, the volume of the liquid between A and C must equal the volume between B and E. The height BE is given in the problem. Let us denote this by letter \(y\text{.}\) Let \(A_1\) and \(A_2\) be the areas on the two ends, where 1 is for the narrow end and 2 for the wide end. Thus, equating the volume of the fluid in AC to that of BE, we must also have

\begin{equation} A_1(h_1 - y) = A_2 y.\tag{17.13} \end{equation}

This gives

\begin{equation*} h_1 = \dfrac{A_2}{A_1 + A_2}\, y. \end{equation*}

Using this in Eq. (17.12) we get

\begin{equation*} h_2 = \dfrac{\rho_1}{\rho_2}\, \dfrac{A_2}{A_1 + A_2}\, y. \end{equation*}

Note that we have ratios of similar quantities, hence, we do not need to convert any units. Putting the numerical values we get

\begin{align*} h_2 \amp = \dfrac{1.0}{0.8}\, \dfrac{4.0}{2.5 + 4.0}\times 2\text{ cm}, \\ \amp = 1.54\text{ cm}. \end{align*}

Multiplying this by \(A_2=4\text{ cm}^2\) will give the volume we need.

\begin{equation*} V_2 = A_2h_2 = 4.0\times 1.54 = 6.16\text{ cm}^3. \end{equation*}

2. Ratio of Heights of Two Fluids on Two Sides of U-tube (JEE, 2020).

An open-ended U-tube of uniform cross-sectional area contains water (density \(10^3\text{ kg m}^{−3}\)). Initially the water level stands at 0.29 m from the bottom in each arm. Kerosene oil (a water-immiscible liquid) of density \(800\text{ kg m}^{−3}\) is added to the left arm until its length is \(0.1\text{ m}\) as shown in Figure 17.18.

The ratio \(\left( \frac{h_1}{h_2} \right)\) of the heights of the liquid in the two arms is (A) \(\frac{15}{14}\text{,}\) (B) \(\frac{35}{33}\text{,}\) (C) \(\frac{7}{6}\text{,}\) (D) \(\frac{5}{4}\text{.}\) (From Indian JEE, 2020.)

Hint.

1. Equate pressure at same level in same fluid. 2. The denser fluid level on the two side goes down on one side by same height as it goies up on the other side.

Answer.

Solution.

When we are in a single fluid, say within the water part, pressure at same horizontal level on the two sides will be same. That is, pressure in water at points A and B in Figure 17.19 will be same.

Thus, we will get the following equation.

\begin{equation*} p_\text{atm} + \rho_1 g h = p_\text{atm} + \rho_2 g \left[ h - \left(h_1 - h_2\right) \right]. \end{equation*}

Simplifying and then dividing both sides by \(\rho_1 h\) we get

\begin{equation} h_1 - h_2 = 0.2 h.\tag{17.14} \end{equation}

From the original level of water (level D in Figure 17.20), we notice that point A would be as much below the original level D as point C will be above D since the two sides have the same area of cross-section.

Using DC = BC/2 and BC from Figure 17.19 gives

\begin{equation*} h_2 - h_0 = \frac{ h - \left(h_1 - h_2\right) }{2} \end{equation*}

Simplifying we have

\begin{equation} h_1 + h_2 = h + 2 h_0.\tag{17.15} \end{equation}

From Eq. (17.14) and (17.15), we get

\begin{equation*} h_1 = 0.6 h + h_0,\ \ h_2 = 0.4 h + h_0. \end{equation*}

Therefore, the ratio is

\begin{equation*} \frac{h_1}{h_2} = \frac{0.6 h + h_0}{0.4 h + h_0}. \end{equation*}

Using the numerical values given,

\begin{equation*} \frac{h_1}{h_2} = \frac{0.6 \times 0.1 + 0.29}{0.4 \times 0.1 + 0.29} = \frac{0.35}{0.33} = \frac{35}{33}. \end{equation*}

This is choice B.

3. U-Tube with Two Different Fluids.

An open U-tube has uniform cross-sectional area of 3 square cm and same height on both ends. Mercury is poured in it till the height from the top is 50-cm. How much water must be poured on one side so that the level of the mercury rises by 1 cm on the other side?

Answer.

\(81.6\, \text{cm}^3\text{.}\)

Solution.

The figure shows the situation after water has been poured in on the left side of the tube so that mercury levels are no longer same on the two sides. Let \(h_1\) be the height of the water in the tube and \(h_2\) be the height of the mercury with respect to its height on the other side of the U-tube. Let us denote the densities of water and mercury by \(\rho_1\) and \(\rho_2\) respectively.

Now we apply Pascal’s principle to the mercury. The pressure at any level in either side of the tube will be the same as long as the two levels are in the same fluid. Refering to the figure we see that the pressure of the level marked \(p_{\textrm{ref}}\) has two expressions, one on the left side using the water height above this reference level and another expression on the right side using the mercury height. Denoting the atmospheric pressure by \(p_0\) we have

\begin{align*} \amp p_{\textrm{ref}} = p_{0} + \rho_1 g h_1,\\ \amp p_{\textrm{ref}} = p_{0} + \rho_2 g h_2. \end{align*}

Therefore,

\begin{equation*} \rho_1 h_1 = \rho_2 h_2 \end{equation*}

Solving for \(h_1\) we obtain

\begin{equation*} h_1 = \left( \frac{ \rho_2}{\rho_1} \right) h_2. \end{equation*}

In the problem statement \(h_2\) is \(2\times 1\) cm since mercury is supposed to rise 1 cm from the instance when the levels were equal on the two sides. Therefore, the height of the water column will be

\begin{equation*} h_1 = \left( \frac{ 13.6\ \textrm{g/cc}}{1.0\ \textrm{g/cc}} \right)2\ \textrm{cm} = 27.2 \ \textrm{cm}. \end{equation*}

Now, the levels on the top on the two sides are 50 cm + 1 cm - 27.2 cm = 23.8 cm on the water-side and 50 cm - 1 cm = 49 cm on the mercury side. The volume of the water poured in will be \(27.2\times 3 = 81.6 \text{cm}^3\text{.}\)

4. U-tube with Three Different Fluids.

Ethyl alcohol is now poured on the other side of the mercury in Exercise 17.4.4.3. How much ethyl alcohol must be poured so that the water level on the other side rises by 1 cm?

Solution.

This would be a three-liquid problem. The figure here shows the situation with the three-liquids in the tube where \(h_3\) is the height of the alcohol. The only liquid with the same liquid on both sides is mercury.

Therefore, we take two points in the mercury, one in the left tube and the other on the right tube that is at the same vertical height as done in the last problem. With \(\rho_3\) denoting the density of the alcohol used in the experiment equating pressure at the same level of mercury on the two sides gives

\begin{equation*} \rho_1 (h_1-h) = \rho_2 (h_2-h) + \rho_3 h_3. \end{equation*}

The heights \(h_1\) and \(h_2\) have been determined in the last problem. Here \(h\) is given to be 1 cm.

\begin{equation*} h_1 = 27.2 \ \textrm{cm};\ \ h_2 = 2\ \textrm{cm};\ \ h = 1\ \textrm{cm} \end{equation*}

The densities are

\begin{equation*} \rho_1 = 1.0 \ \textrm{g/cm}^3;\ \ \rho_2 = 13.6 \ \textrm{g/cm}^3;\ \ \rho_3 = 0.81 \ \textrm{g/cm}^3. \end{equation*}

Therefore,

\begin{equation*} h_3 = 15.6\ \textrm{cm}. \end{equation*}

Prev Top Next