Length Contraction

Section 49.8 Length Contraction

We define length of a rod as the distance between the positions of the two ends at the same time. The caveat that the positions of the two ends be know at the same time in the frame in which we seek the length is important since time and position are connected in Lorentz transformations. Below we will apply Lorentz transformation to seek length in a frame in which rod is moving.

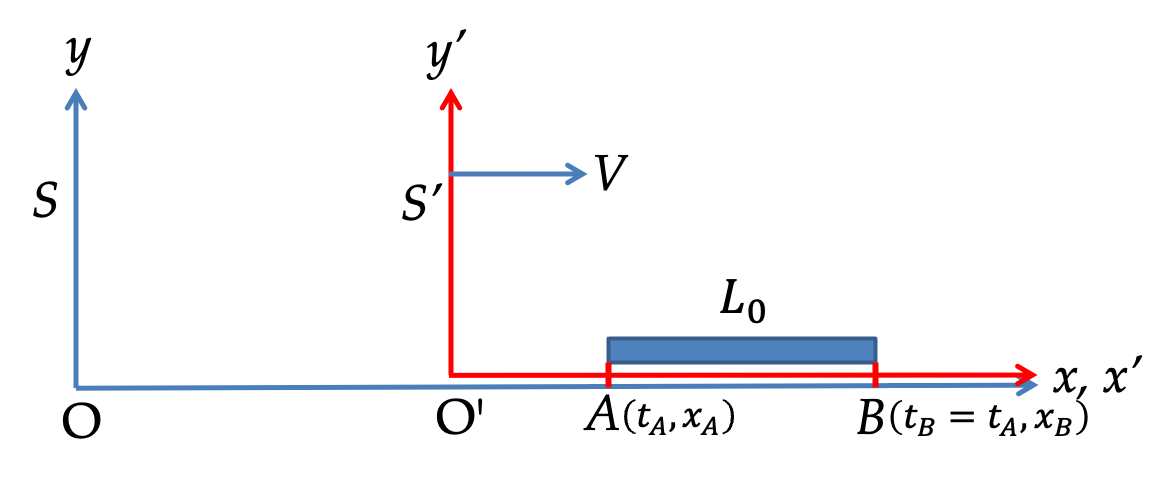
For simplicity, we consider rod along \(x\) axis, which is the direction of the relative motion of frames as shown in Figure 49.30. We consider rod to be at rest in frame S’ with ends A and B with events \((t'_A, x'_A)\) and \((t'_B=t'_A, x'_B \gt x'_A)\text{,}\) respectively. In frame S’, we define length by

\begin{equation*} L_0 = x'_B - x'_A. \end{equation*}

Figure 49.30. Length \(L_0\) is defined as \(|x'_B-x'_A|\) when \(t'_B=t'_A\) for events A and B.

To calculate length of the rod in frame S, we first find Lorenz transformation of events A and B. During calculation we will keep \(t'_A\) and \(t'_B\) separate even though they are equal in our calculations. This helps keeping track of the two events.

\begin{align*} \amp t_A = \gamma \left( t'_A + V x'_A/c^2 \right),\ \ x_A = \gamma \left( x'_A + V t'_A \right) \\ \amp t_B = \gamma \left( t'_B + V x'_B/c^2 \right),\ \ x_B = \gamma \left( x'_B + V t'_B \right) \end{align*}

We want \(x_B-x_A\) when \(t_B=t_A\text{.}\) Towards that end, let us express \(t'_A\) and \(t'_B\) in terms of \(t_A\) and \(t_B\) by using the first set of these equations.

\begin{equation*} t'_A = \frac{t_A}{\gamma} - V x'_A/c^2,\ \ t'_B = \frac{t_B}{\gamma} - V x'_B/c^2. \end{equation*}

Therefore,

\begin{align*} x_B - x_A \amp = \gamma \left[ x'_B + \frac{V t_B}{\gamma} - \frac{V ^2}{c^2}x'_B\right] - \gamma \left[ x'_A + \frac{V t_A}{\gamma} - \frac{V ^2}{c^2}x'_A\right] \\ \amp = \gamma \left[ x'_B - x'_A - \frac{V ^2}{c^2}\, \left(x'_B - x'_A \right)\right] + \frac{V}{\gamma}\left( t_B - t_A \right) \end{align*}

This will give length if \(t_B=t_A\) in this frame (S). Denoting \(x_B-x_A\) by \(L\) since we have denoted \(x'_B - x'_A\) by \(L_0\text{,}\) we have

\begin{align*} L\amp = \gamma \left( 1 - \frac{V^2}{c^2} \right) \, L_0. \end{align*}

With \(\gamma = 1/\sqrt{1-V^2/c^2}\text{,}\) this is

\begin{equation} L = \dfrac{L_0}{\gamma} = L_0\,\sqrt{ 1 - \dfrac{V^2}{c^2} }.\tag{49.47} \end{equation}

This is called length cortaction. Since \(\gamma \gt 1\text{,}\) length of a rod will be smaller in a frame in which rod is moving, i.e., \(L \le L_0\text{.}\)

Since \(y\) and \(z\) coordinates do not change, the transverse dimensions, i.e., the dimensions of the rod perpendicular to the direction of the motion of the rod are unaffected. Let us denote these dimensions with a subscript \(\perp\text{.}\)

\begin{equation} L_{\perp} = L_{0\perp}.\tag{49.48} \end{equation}

Checkpoint 49.31. Relation of Distance in Two Spaceships in Relative Motion.

Same two observers as in Exercise Checkpoint 49.23. A rod of length \(1\:\textrm{m}\) is laid out on the \(x\)-axis in the frame of A from origin to \((x =1\: \textrm{m}, 0,0)\text{.}\) What will be the length of the rod observed by an observer in frame of spaceship B?

Hint.

Answer.

Solution.

We use length contraction to answer this.

\begin{equation*} L_B = \frac{L_A}{\gamma} = \frac{\sqrt{3}}{2}\times 1\text{ m} = 0.866\text{ m}. \end{equation*}

Checkpoint 49.32. Size of a spaceship.

A spaceship is seen to move past an observer on Earth at a speed of \(0.95 c\text{,}\) i.e. at \(95\%\) of the speed of light in the direction parallel to the length of the ship. An astronaut in the spaceship has measured the length of the spaceship to be 100 m. What will be the length of the spaceship as observed by the observer on Earth?

Hint.

Use length contraction formula.

Answer.

\(31.3\:\textrm{m}\text{.}\)

Solution.

The length 100 m for the spaceship is the length in the rest frame of the ship. The length observed by the Earth-based observer will be in the lab frame. From our discussion above the lab frame value will be contracted compared to the rest frame value by a factor of \(\gamma\text{.}\) Here \(\gamma\) has the following value.

\begin{equation*} \gamma = \frac{1}{\sqrt{1-V^2/c^2}} = \frac{1}{\sqrt{1-0.95^2}} = 3.2. \end{equation*}

Therefore, the length observed by the observer on Earth will be

\begin{equation*} L = \frac{L_0}{\gamma} = \frac{100\: \textrm{m}}{3.2} = 31.3\:\textrm{m}. \end{equation*}

Checkpoint 49.33. Relation of Duration and Distance in Two Spaceships in Relative Motion.

Same two observers as in Exercise Checkpoint 49.23. But, now we look at two events occurring in spaceship A. A photon arrives at the origin of A at its time \(t=0\) and another photon arrives at \((x =1\: \textrm{m}, 0,0)\) at \(t=0\) in the frame of ship A. (a) Find the coordinates and times of the two events as observed by frame B. (b) In which frame, the two events are simultaneous and in which frame they are not simultaneous?

Hint.

Answer.

(a) \(1.92 \times 10^{-9}\text{ sec}\text{,}\) \(1.155\text{ m}\text{,}\) (b) Simultaneous in A.

Solution. (a)

(a) Now, the events are in frame A, which is moving towards positive \(x\) axis when observed from frame B. The event of photon arriving at origin at \(t_A=0\) will be also origin of B at \(t_B=0\) since the two frames were set that way. The other event of photon at \(x_A = 1\text{ m}\) at \(t_A=0\) will have \(t_B\) and \(x_B\) as follows.

\begin{align*} t_B \amp = \gamma\left( t_A + x_A V/c^2\right)\\ \amp = \sqrt{2}{\sqrt{3}}\times \frac{1}{2\times 3 \times 10^{8}} = 1.92 \times 10^{-9}\text{ sec}. \end{align*}

\begin{align*} x_B \amp = \gamma\left( x_A + V t_A\right) = \sqrt{2}{\sqrt{3}}\times 1 = 1.155\text{ m}. \end{align*}

Prev Top Next