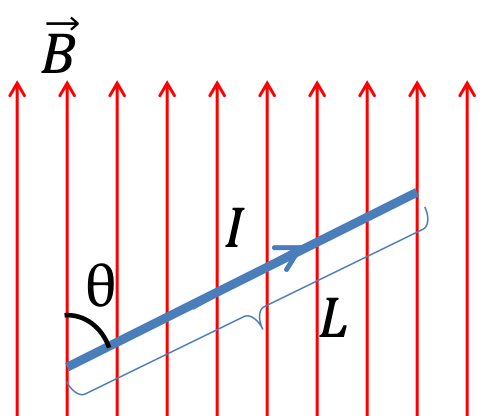
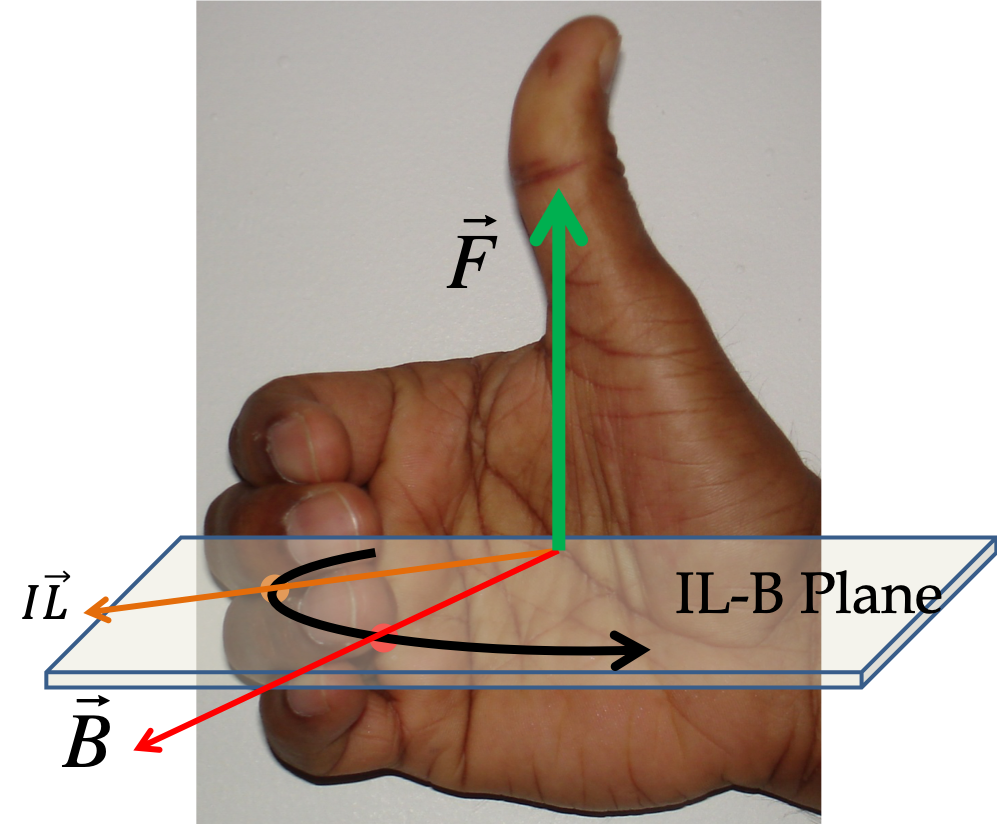
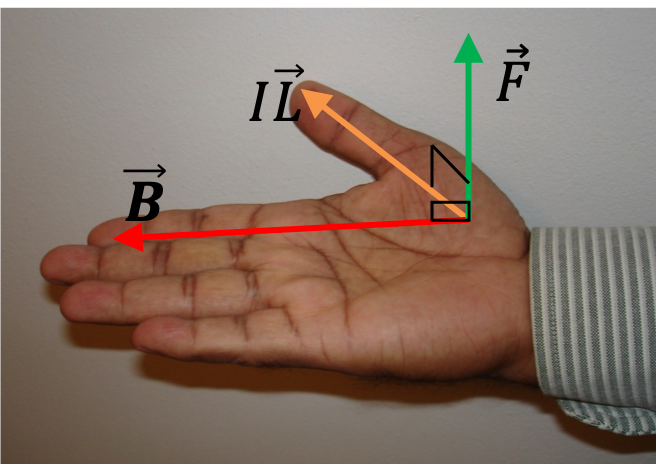
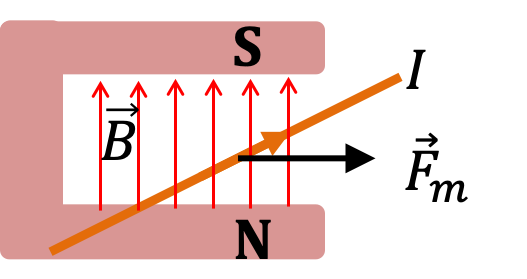
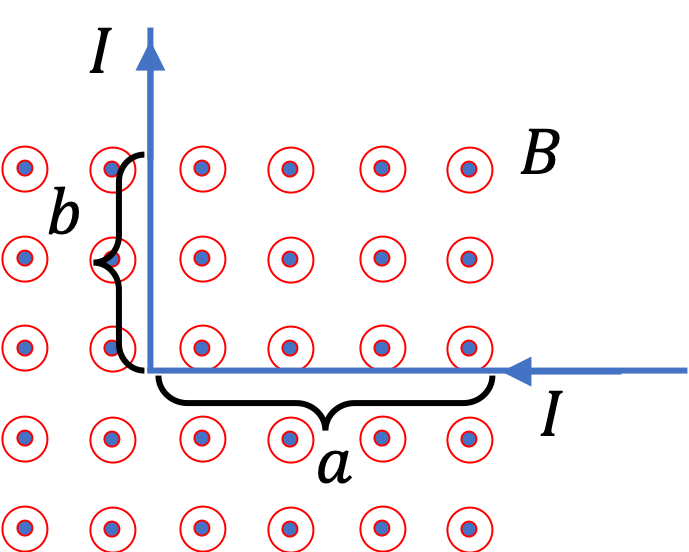
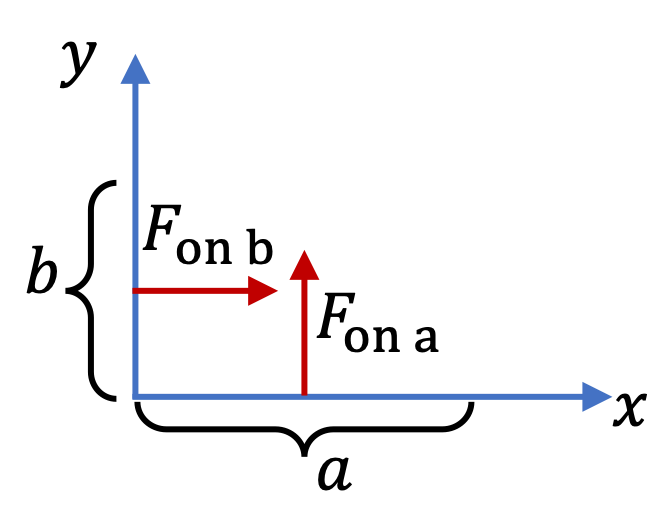
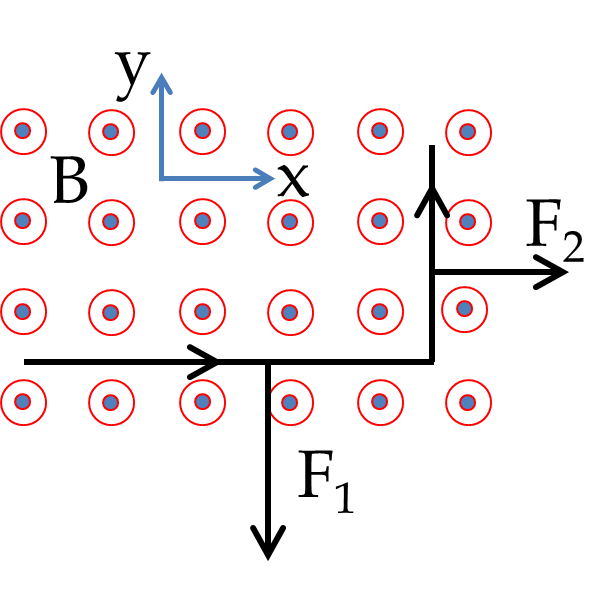
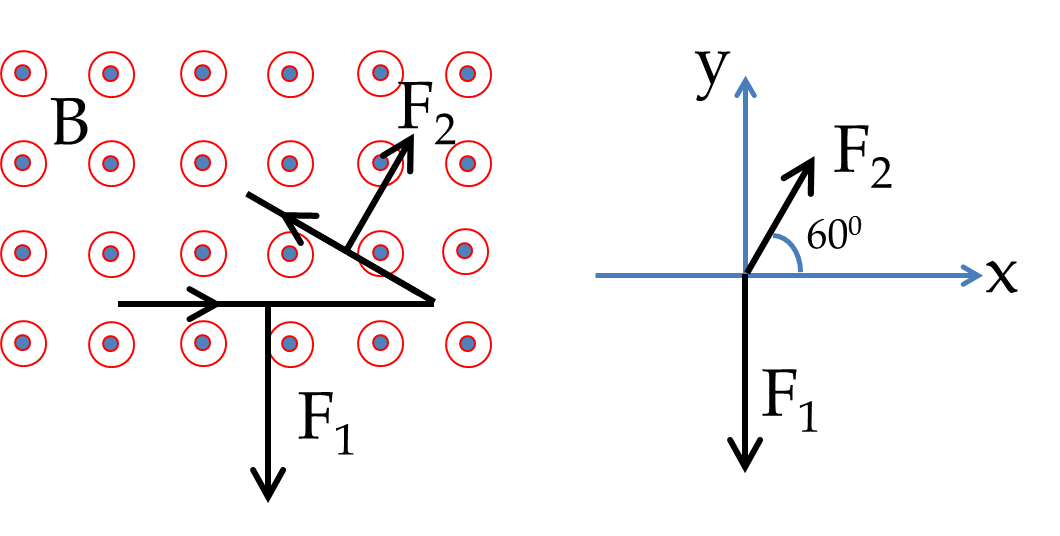
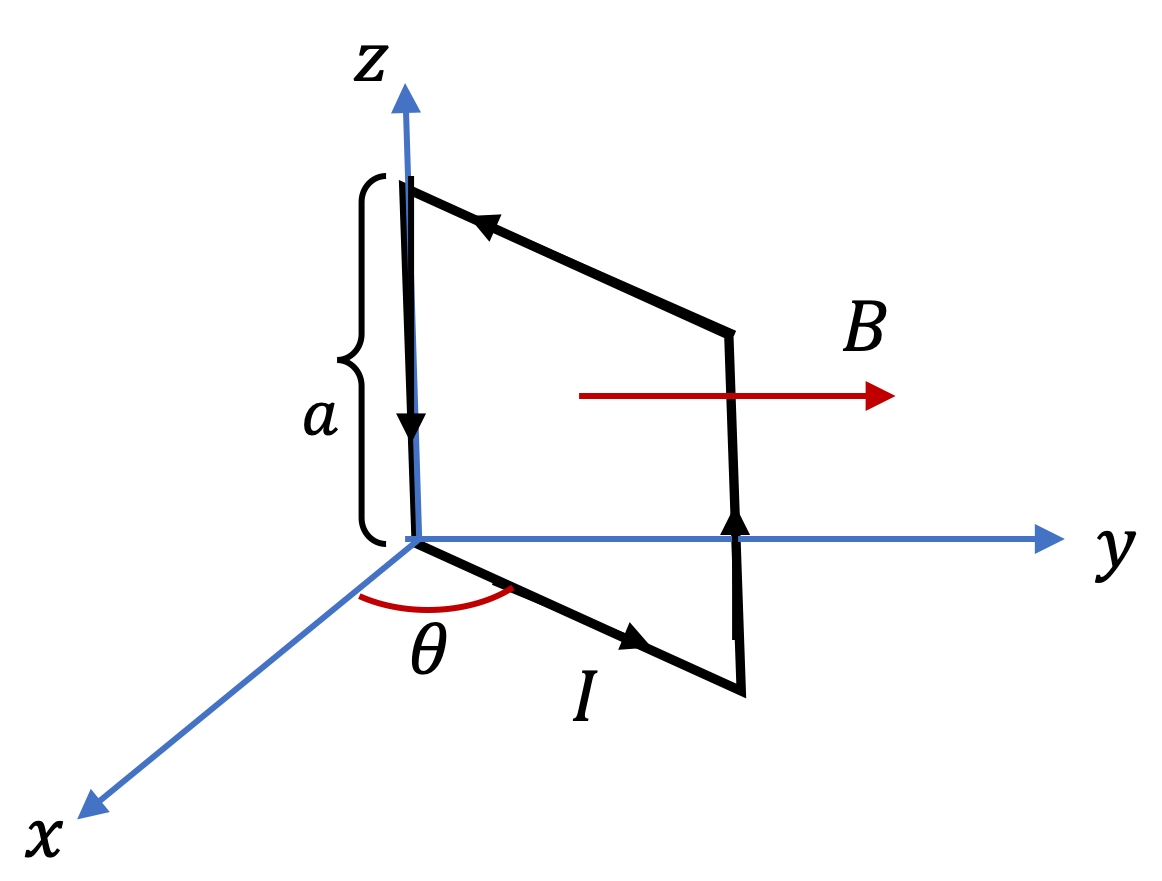
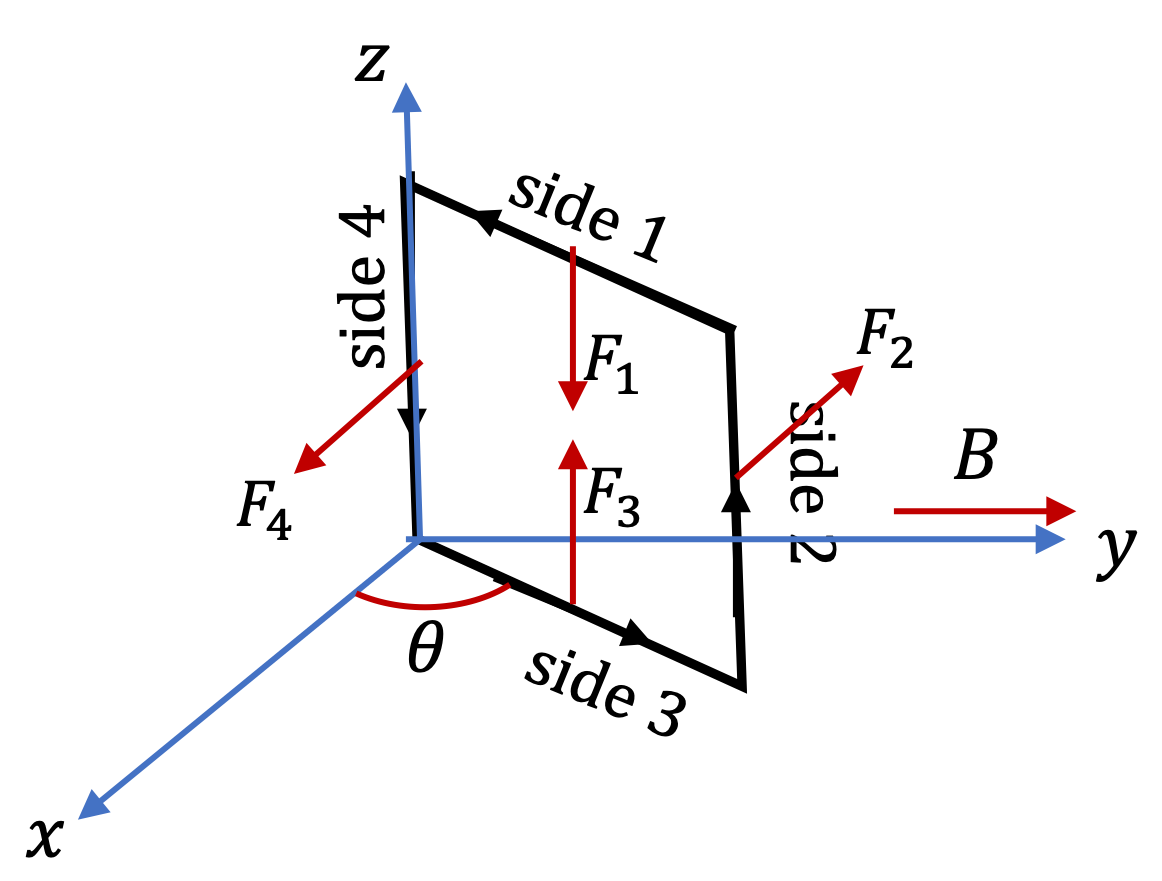
By using the formula \(\vec F_m = I\vec L\times \vec B\) on each straight segment, we find that the magnitudes of the forces on them are
\begin{align*}
F_{1} \amp = 5\:\text{A}\times 0.06\:\text{m}\times 2.0\:\text{T} = 0.6\text{ N}.\\
F_{2} \amp = 5\:\text{A}\times 0.04\:\text{m}\times 2.0\:\text{T}=0.4\text{ N}.
\end{align*}
The net force is not \((0.6\text{ N} + 0.4\text{ N})\) since the forces are not in the same direction. We need to add them vectorially. We will do that analytically by using the coordinate system shown in the figure. The \(x\) and \(y\) components of the forces \(\vec F_1\) and \(\vec F_2\) are
\begin{align*}
\amp F_{1x} = 0,\ \ F_{1y} = - 0.6\:\text{N}. \\
\amp F_{2x} = 0.2 \:\text{N},\ \ F_{2y} = 0.35\:\text{N},
\end{align*}
The \(x\) and \(y\) components of the net force are
\begin{equation*}
F_x = 0.20\:\text{N},\ \ F_{y} = -0.25\:\text{N}.
\end{equation*}
The magnetic force has a magnitude of
\begin{equation*}
\sqrt{0.20^2 + 0.25^2} = 0.32\:\text{N},
\end{equation*}
and is pointed in the 4-th quadrant at an angle of \(51.3^{\circ}\) clockwise from the positive \(x\) axis.