Energy

Section 8.6 Energy

The sum of kinetic and potential energies from all applicable conservative forces on an object is called energy of the object. We usually denote energy by the capital letter \(E \text{.}\)

\begin{equation} E = K + \sum U.\tag{8.35} \end{equation}

Here the symbol \(\sum\) (read sigma) stands for the process of summation over all sources of potential energies \(U\text{.}\) For instance, if a block is attached to a spring and swings vertically, \(\sum U\) will be \(U_\text{weight} + U_\text{spring}\text{.}\)

Subsection 8.6.1 Energy of a Particle Subject to Gravity

For instance, if our system is a particle of mass \(m\) moving with speed \(v \) at some instant \(t \text{,}\) and is subject to only the force of gravity. Then, with positive \(y\) axis pointed up, its potential energy will be

\begin{equation*} U = mgy. \end{equation*}

Therefore, the energy of this particle at this instant will be

\begin{equation*} E = \dfrac{1}{2}mv^2 + mgy. \end{equation*}

Subsection 8.6.2 Energy of a Particle Subject to Gravity and Spring Forces

Now, suppose, the aforementioned particle was attached to a spring of spring constnat \(k \text{.}\) Let the spring at instant \(t\) was either compressed or stretched by \(\Delta l\text{.}\) Then, the potential energy would be a sum of the potential energies due to gravity and due to the spring force.

\begin{equation*} U = mgy + \dfrac{1}{2}k \left( \Delta l\right)^2. \end{equation*}

Therefore, energy of this particle will be

\begin{equation*} E = \dfrac{1}{2}mv^2 +mgy + \dfrac{1}{2}k \left( \Delta l\right)^2. \end{equation*}

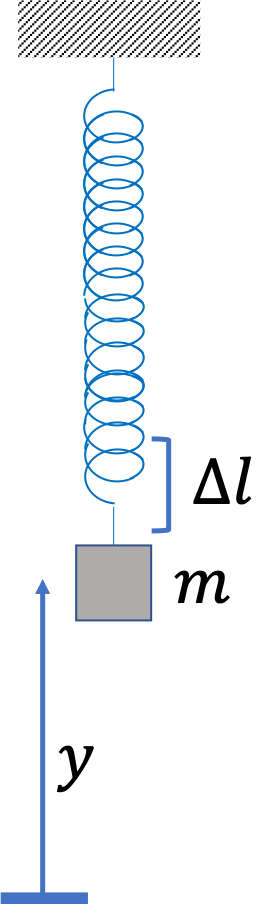
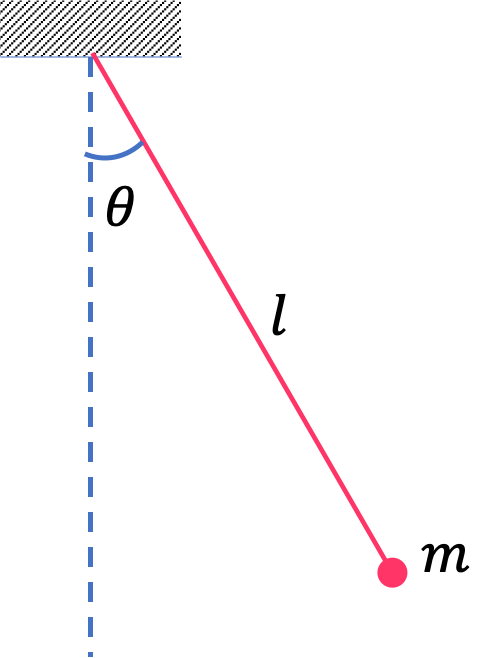
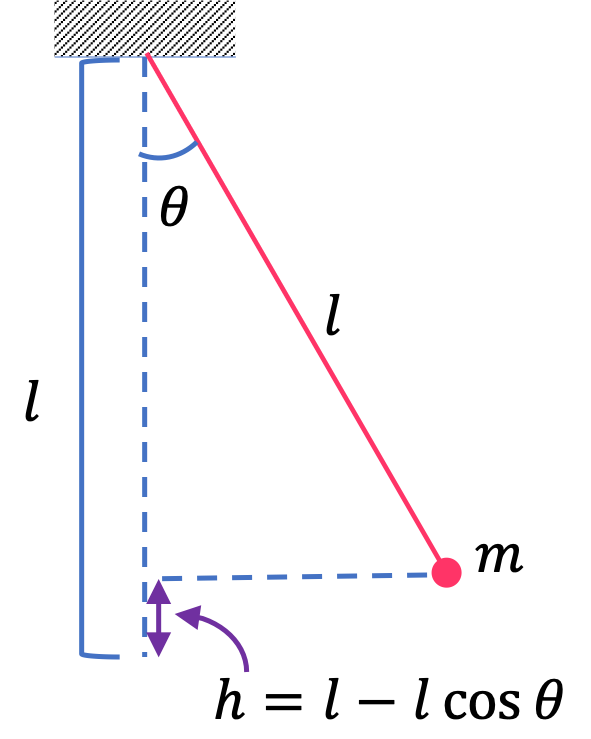
Remark 8.43. Definition of Energy as a Guide.

The definition of energy, as sum of kinetic and potential energies, given in Eq. (8.35) is a guide for you to find the actual expression in your particular situation. In each situation, you would need to ask, what are the conservative forces, and set up coordinates or variables that are necessary for properly expressing protential energy.

Example 8.44. Energy of a Car on a Hill.

A car of mass \(2,000 \text{ kg}\) is moving up a hill at a speed of \(25 \text{ m/s} \) as shown in Figure 8.45. The angle of inclination of the hill is \(10^{\circ}\text{.}\) If the bottom of the hill is chosen to be the zero of gravitational potential energy, what is the energy of the car when it is at a location that is \(150\text{ m}\text{,}\) as measured on the incline, from the bottom of the hill?

Answer.

\(1,136,000\text{ J}\text{.}\)

Solution.

The energy will be the sum of kinetic and potential energies. For potential energy due to gravity, we need height from the zero reference. Here \(h = 150\text{ m} \times \sin\,10^{\circ} = 26.05\text{ m}.\) Therefore, energy is

\begin{align*} E \amp = \dfrac{1}{2}mv^2 + m g h, \\ \amp = \dfrac{1}{2}\times 2,000\times 25^2 + 2,000\times 9.81\times 26.05, \\ \amp = 625,000+ 511,000 = 1,136,000\text{ J}, \end{align*}

where I have rounded to four significant figures.

Example 8.46. Energy of a Pendulum With Zero of Potential Energy at Equilibrium.

A plane pendulum of length \(l\) is oscillating about its equilibrium. Let \(\theta\) be the angular displacement from vertical at an arbitrary instant. The pendulum bob has mass \(m\) and has speed \(v \) at this instant. What is the energy of the pendulum bob?

Answer.

\(\dfrac{1}{2}m v^2 + m g \left( l - l \, \cos\, \theta \right)\text{.}\)

Solution.

The figure here shows height \(h\) of the bob from the zero potential energy reference, which happens when the pendulum is vertical. From the adjacent side of the triangle and the length of the string, we get

\begin{equation*} h = l - l \, \cos\, \theta. \end{equation*}

The gravitational potential energy will be \(m g h\text{.}\) The energy of the pendulum bob will be

\begin{equation*} E = \dfrac{1}{2}m v^2 + m g \left( l - l \, \cos\, \theta \right). \end{equation*}

Example 8.47. Energy of a Block Attached to Two Springs.

A block of mass \(m\) is attached to two springs of spring constants \(k_1 \) and \(k_2\) as shown in Figure 8.48. When the block is in the middle, the two springs are neither stretched nor compressed.

When block is pulled to one side, one of the spring is compressed while the other is stretched by the same amount. At some point in time, the block has a speed \(v\) and at that instant the spring with spring constant \(k_1 \) is stretched by an amount \(d\text{.}\) Assume the block moves on a horizontal frictionless table.

What is the energy of the block at this instant?

Answer.

\(\dfrac{1}{2} m v^2 + \dfrac{1}{2} k_1 d^2 + \dfrac{1}{2} k_2 d^2 \) .

Solution.

We add kinetic energy to the two potential energy terms, from the two conservative forces by the two springs.

\begin{equation*} E = \dfrac{1}{2} m v^2 + \dfrac{1}{2} k_1 d^2 + \dfrac{1}{2} k_2 d^2. \end{equation*}

Example 8.49. Energy of the Moon.

The potential energy due to gravitational force between two bodies is given by the formula:

\begin{equation*} U = - G\dfrac{m_1m_2}{r}. \end{equation*}

At some instant Moon is a distance \(r_{em}\) from the Earth and a distance \(r_{sm}\) from the Sun. At this instant the speed of Moon is \(v_m\text{.}\) Let \(M_m,\ M_e,\ M_s\) be the masses of the Moon, the Earth, and the Sun. What is the energy of Moon?

Answer.

\(\dfrac{1}{2}\,M_m\, v_m^2\) \(-G\, M_m \left( \dfrac{M_e}{r_{em}} + \dfrac{M_s}{r_{sm}} \right) \) .

Solution.

We add kinetic energy to the two potential energy terms, one due to force by the Earth and the other the force by the Sun.

\begin{equation*} E_m = \dfrac{1}{2}\,M_m\, v_m^2 -G\, M_m \left( \dfrac{M_e}{r_{em}} + \dfrac{M_s}{r_{sm}} \right). \end{equation*}

Prev Top Next