Example 24.20. Work Done by an Ideal Gas in an Adiabatic Process.
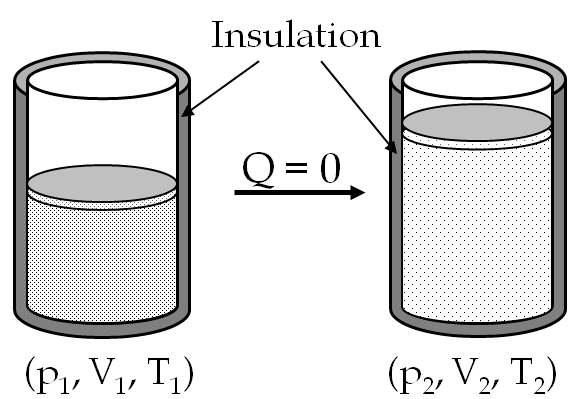
A gas cylinder with a movable piston contains \(n\) moles of an ideal monatomic gas in state \((p_1, V_1, T_1)\text{.}\) The cylinder is surrounded by an ideal insulating material to thermally insulate the gas. The piston is then pulled to expand the gas. We find that the temperature of the gas goes down. The final state of the gas is \((p_2, V_2, T_2 \lt T_1)\text{.}\) What is the work done by-the-gas? Use the following fact: In a thermally insulated process, also called an adiabatic process the changes in pressure and volume are related by \(pV^\gamma = \text{constant}\text{,}\) where \(\gamma=c_p/c_V\text{.}\) For ideal gas monatomic gas, \(\gamma = 5/3\text{.}\) Monatomic gas such as helium contain one atom per molecule.
Answer.
\(\frac{1}{\gamma - 1} \left(p_2 V_2 - p_1 V_1 \right)\text{.}\)
Solution.
The process is given by \(pV^\gamma = \text{constant} \equiv A\text{,}\) where the constant can be written by the values of \(p\) and \(V\) in the initial state or in the final state. Thus we have on the process
\begin{equation*}
p = \frac{A}{V^\gamma},\ \ \text{with}\ \ A=p_1V_1^\gamma = p_2V_2^\gamma.
\end{equation*}
Now, by replacing this \(p\) in the work formula we get
\begin{equation*}
W_{12} = -\int\, \frac{A}{V^\gamma}\, dV = \frac{A}{\gamma - 1}\left( V_2^{-\gamma+1} - V_1^{-\gamma+1} \right).
\end{equation*}
Bringing \(A\) inside the parenthesis and using
\begin{align*}
\amp AV_2^{-\gamma+1} = p_2V_2^\gamma V_2^{-\gamma+1} = p_2 V_2 \\
\amp AV_1^{-\gamma+1} = p_1V_1^\gamma V_1^{-\gamma+1} = p_1 V_1
\end{align*}
Hence, we get
\begin{equation*}
W_{12} = \frac{1}{\gamma - 1} \left(p_2 V_2 - p_1 V_1 \right).
\end{equation*}