Tracking Motion
1. A Boy Running On a Straight Track Uniformly.
Follow the link: Example 2.6.
2. From \(x \) Versus \(t \) Plot to Motion Diagram.
Follow the link: Example 2.9.
Section 2.10 One-Dimensional Motion Bootcamp
Exercises Exercises
Position, Displacement, and Distance
3. Difference between Displacement and Distance.
Follow the link: Example 2.14.
Speed and Velocity
4. Constant Speed Warmup.
Follow the link: Example 2.16.
5. Average Velocity versus Average Speed.
Follow the link: Exercise 2.4.6.1.
6. Average Speed and Average Velocity in a Motion with Turnaround.
A truck travels north at a constant speed on a straight North-South road covering a distance of \(35\ \text{km}\) in \(30\ \text{min}\text{.}\) The driver realizes that he forget to pick up a package, and turns the truck around, and heads straight back to the original place. It took him \(25\ \text{min}\) on the return trip. Find the displacement, average speed and average velocity for the entire trip. Express your speed and velocity in km/h.
Answer.
Displacement = 0, Average Velocity = 0, Average Speed = \(76.4\ \text{km/h}\text{.}\)
7. Velocity from a Graph.
Follow the link: Example 2.27.
8. Two Cars Moving Towards Each Other on a Straightline.
Two cars travel on a straight East-West road. Initially the cars are \(150\, \text{km}\) apart. Both cars travel at a constant speed of \(60\, \text{km/h}\) with respect to the ground; Car A heads to the east and B to the west. (a) Write the average velocity of the two cars using x-axis in the East-Wast direction, taking the direction to the East direction as positive. (b) Find the displacements of the two cars when each has traveled 50 km. (c) Find the time it takes each car to travel 50 km. (d) Find the time when they are 50 km apart if the time is zero when they were 150 km apart.
Answer.
(a) \(v_{A} = +60\, \text{km/h}\text{,}\) \(v_{B} = -60\, \text{km/h}\text{.}\) (b) \(v_{A} = +50\, \text{km/h}\text{,}\) \(v_{B} = -50\, \text{km/h}\text{.}\) (c) \(50\,\text{s}\text{.}\) (d) \(75\,\text{s}\text{.}\)
Solution 1. a
From the description, A is going East (\(+x\)-direction). Therefore,
\begin{equation*}
v_{Ax} = +60\, \text{km/h}.
\end{equation*}
But, since B is moving West (\(-x\)-direction),
\begin{equation*}
v_{Bx} = -60\, \text{km/h}.
\end{equation*}
You can drop subscript \(x\) in these symbols as long as you have clearly stated positive and negative directions.
Solution 2. b
ASince the difference \(x_f - x_i\) will be positive for A but negative for B, their displacements will be
\begin{align*}
\amp \Delta x_A = + 50\,\text{km}\\
\amp \Delta x_B = - 50\,\text{km}
\end{align*}
Solution 3. c
For time, only the average speed matters. Here it is \(v=60\, \text{km/h}\) for both. Hence, time will be same for both given by
\begin{equation*}
\Delta t = \frac{50\,\text{km}}{60\, \text{km/h}} = \frac{50\,\text{km}}{1\, \text{km/s}} = 50\,\text{s}.
\end{equation*}
Solution 4. c
For them to be \(50\,\text{km}\) apart at the end, each must have moved \(75\,\text{km}\) since they were \(150\,\text{km}\) apart initially and they are moving towards each other. Hence, time will be
\begin{equation*}
t = \frac{75\,\text{km}}{60\, \text{km/h}} = 75\, \text{s}.
\end{equation*}
9. Two Runners Running Towards Each Other With Different Speeds.
Two runners A and B start out at two ends of a \(100\text{-m}\) straight track, and run at constant speeds. Runner A has a speed of \(30\ \text{km/h}\) and runner B has a speed of \(20\ \text{km/h}\text{.}\) Where and when they would meet?
Answer.
\(60\,\text{ m} from A\) at \(7.2\,\text{s}\text{.}\)
Solution.
Let us place A at origin and B at \(x=100\,\text{m} = 0.100\,\text{km}\) at \(t=0\text{.}\) Let they meet at \(x=d\) (km) at \(t=T\) (h). Clearly,
\begin{align*}
\amp d = 30 T,\\
\amp 0.100- d = 20 T.
\end{align*}
We need to solve for \(d\) and \(T\text{.}\) Adding them we get
\begin{equation*}
T = \frac{0.100}{50} = 2\times 10^{-3}\,\text{h}.
\end{equation*}
Then,
\begin{equation*}
d = 30 \times 2 \times 10^{-3} = 0.060\,\text{ km} = 60\,\text{ m}.
\end{equation*}
That is, they will meet \(60\,\text{ m}\) from A. Let’s also write \(T\) in seconds.
\begin{equation*}
T = 2\times 10^{-3} \times 3600 = 7.2\,\text{s}.
\end{equation*}
10. Train Moving With Varying Speed Between Stations.
A subway train travels on a straight rail between two stations. Taking one of the stations as the origin of \(x\)-axis the position of the train versus time is plotted as displayed in Figure 2.76. Estimate the displacement, average velocity and average speed for the following intervals. (a) \([0, 5\,\text{min}]\text{,}\) (b) \([5 \,\text{min}, 15 \,\text{min}]\text{,}\) (c) \([15\,\text{min}, 25 \,\text{min}]\text{,}\) (d) \([25 \,\text{min}, 45\,\text{min}]\text{,}\) and (e) \([45\,\text{min}, 50 \,\text{min}]\text{.}\)
Answer.
See the solution.
Solution.
For concreteness of discussing the direction, let A to B direction be the North direction.
| Interval | Displacement | Average Velocity | Average Speed |
|---|---|---|---|
| (0, 5 min) | 0 | 0 | 0 |
| (5 min, 15 min) | 300 m, North | 30 m/min, North | 30 m/min |
| (15 min, 25 min) | 0 | 0 | 0 |
| (25 min, 45 min) | 300 m, South | 15 m/min, South | 15 m/min |
| (45 min, 50 min) | 0 | 0 | 0 |
| (0 min, 50 min) | 0 | 0 | 12 m/min |
11. Train Repeating Motion on Straight Track Between Same Stations.
A train runs on a straight track all day repeating its route every \(60\) minutes, stopping at only the designated stations. Placing the origin at one of the stations and the \(x\)-axis on the track, the position of the train is recorded as its \(x\)-coordinate. Figure 2.77 shows a plot of the \(x\)-coordinate of the train with time.
- Assuming the train stops only at the stations, how many stations are there in the train’s route?
- For how long does the train stop at each station?
- What are the average velocities of the train between different stations? Give the magnitude and direction between pairs of the stations which are visited successively.
- What is the average velocity over any \(60\)-minute interval?
- What is the average speed over any \(60\)-minute interval?
Answer.
(a) 5, (b) 10 min, (c) \(12, 24, -24, -48, 48\) in km/h, (d) 0, (e) \(16\,\text{km/h}\text{.}\)
Solution 1. a
When you look at the figure, position does not change for a while at 4 locations, which we assume are the stations. Assuming the origin was also a station, we will get 5 stations for the answer.
Solution 2. b
From the time-axis, it’s clear the train stops at each station for 10 minutes.
Solution 3. c
We will give directions as positive or negative, positive is the direction towards positive \(x\)-axis. \(2\,\text{km}/10\,\text{min} = 12\,\text{km/h}\text{,}\) \(2\,\text{km}/5\,\text{min} = 24\,\text{km/h}\text{,}\) \(-4\,\text{km}/10\,\text{min} = -24\,\text{km/h}\text{,}\) \(-4\,\text{km}/5\,\text{min} = -48\,\text{km/h}\text{,}\) \(4\,\text{km}/5\,\text{min} = 48\,\text{km/h}\)
Solution 4. d
zero since displacement is zero.
Solution 5. e
Total distance travelled = \(2 + 2 + 4 + 4 + 4 = 16\, \text{km}\text{.}\) This covered in 60 min or 1 hr. Therefore, average speed is \(16\,\text{km/h}\text{.}\)
12. Obtaining Velocity from Position Versus Time Graph.
The \(x\)-coordinate of a moving object varies in time according to the graph shown in Figure 2.78, while the \(y\) and \(z\)-coordinates do not change with time. Assume the corners in the figure to be smooth. Determine the instantaneous velocity at the following instants (i) \(t = 0\text{,}\) (ii) \(t = 5\) min, (iii) \(t = 15\) min, (iv) \(t = 35\) min, and (v) \(t = 45\) min.
Answer.
\(v_x(0) = 23\, \text{m/min} = v_x(15\,\text{min})\text{,}\) \(v_x(15\text{ min}) = 0 = v_x(45\text{ min})\text{,}\) \(v_x(35\text{ min}) = 23\, \text{m/min} = - 40\text{ m/min}\text{.}\)
Solution.
From the slopes at the correponding points we find the following values for the \(x\)-component of the velocity. \(v_x\)(0) = \(v_x\)(5 min) = 300 m/13 min = 23 m/min, \(v_x\)(15) = \(v_x\)(45 min) = 0, and \(v_x\)(35 min) = (-400-300) m/(37.5-20) min = - 40 m/min.
13. Obtaining Velocity from Height Versus Time Graph.
A boy throws a ball straight up. The vertical position of the ball is given by the \(y\)-coordinate in a coordinate system in which the positive \(y\)-axis is pointed up and the origin is at the point where the ball leaves the hand. The \(x\) and \(z\)-coordinates of the ball do not change with time. The \(y\)-coordinate of the ball as a function of time is shown in Figure 2.79.
(a) From the graph, estimate the instantaneous velocity of the ball at the following instants in time. (i) \(t = 0\text{,}\) (ii) \(t = 0.4\) sec, (iii) \(t = 1\) sec, (iv) \(t = 1.2\) sec, and (v) \(t = 2\) sec.
(b) From the graph, estimate the average velocity between the following intervals. (i) \([0,0.4\ \textrm{sec}]\text{,}\) (ii) \([0,1\ \textrm{sec}]\text{,}\) (iii) \([0.4\ \textrm{sec},1\ \textrm{sec}]\text{,}\) (iv) \([1\ \textrm{sec}, 1.2\ \textrm{sec}]\text{,}\) and (v) \([0.4\ \textrm{sec} , 2\ \textrm{sec}]\text{.}\)
Hint.
(a) Find slopes of tangents. (b) find slopes of secants.
Answer.
See solution.
Solution 1. a
The \(y\)-component of the instantaneous velocity of the ball can be determined from the slopes of the tangent to the given plot of \(y\) versus \(t\text{.}\) The right-angled triangles at the instants in question are drawn whose hypotenuse is tangent to the plot.
From the triangles shown in the figure, you can easily find the slopes to be
\begin{align*}
\amp \text{at } t = 0: v_y = \frac{3.0}{0.2} = 15\text{ m/s}.\\
\amp \text{at } t = 0.2\text{ s}: v_y = \frac{1.6}{0.2} = 8\text{ m/s}.\\
\amp \text{at } t = 1.0\text{ s}: v_y = \frac{0}{\text{any non-zero interval}} = 0\text{ m/s}.\\
\amp \text{at } t = 1.2\text{ s}: v_y = \frac{-0.8}{0.6} = -1.33\text{ m/s}.\\
\amp \text{at } t = 2.0\text{ s}: v_y = \frac{-3.0}{0.34} = -8.8\text{ m/s}.
\end{align*}
Solution 2. b
\begin{align*}
\amp \text{from } 0 \text{ to } 0.4\text{ s}: \Delta t = 0.4,\ \Delta y = 0.34,\, v_{\text{ave},y} = 0.85\text{ m/s}.\\
\amp \text{from } 0 \text{ to } 1.0\text{ s}: \Delta t = 1.0,\ \Delta y = 5.5,\, v_{\text{ave},y} = 5.5\text{ m/s}.\\
\amp \text{from } 0.4 \text{ to } 1.0\text{ s}: \Delta t = 0.6,\ \Delta y = 5.16,\, v_{\text{ave},y} = 8.6\text{ m/s}.\\
\amp \text{from } 1.0 \text{ to } 1.2\text{ s}: \Delta t = 0.2,\ \Delta y = -0.1,\, v_{\text{ave},y} = -0.5\text{ m/s}.\\
\amp \text{from } 0.4 \text{ to } 2.0\text{ s}: \Delta t = 1.6,\ \Delta y = 0.86,\, v_{\text{ave},y} = 0.54\text{ m/s}.
\end{align*}
14. Velocity from Position Given as a Function of Time.
Follow the link: Exercise 2.4.6.4.
15. (Calculus) Velocity from Derivative.
Follow the link: Exercise 2.4.6.5.
Acceleration
16. Analyzing an Experimental Data from Motion Detectors.
Follow the link: Exercise 2.5.5.1.
17. Practice with a Friend : Analyze the Experiment.
Follow the link: Exercise 2.5.5.2.
18. (Calculus) Velocity and Acceleration from Derivative.
Follow the link: Example 2.44.
19. Using slope of \(v_x \) to compute \(a_x \).
Follow the link: Example 2.47.
20. Compute \(\Delta v_x \) from \(a_x\) versus \(t \) plot.
Follow the link: Example 2.50.
Displacement from Velocity
21. Compute \(\Delta x \) from \(v_x \) versus \(t \) plot.
Follow the link: Exercise 2.4.6.2.
22. Displacement from \(v_x \) vs \(t \) Graph.
Follow the link: Exercise 2.4.6.3.
23. (Calculus) Determining \(\Delta y\) from Given \(v_y(t)\).
Follow the link: Exercise 2.4.6.6.
Constant Acceleration Motion
24. Constant Acceleration Warmup.
Follow the link: Example 2.60.
25. Stopping Distance in a Constant Deceleration Situation.
Follow the link: Example 2.62.
26. Constant Acceleration Down an Incline.
Follow the link: Example 2.63.
27. Deceleration of a Hockey Puck While Moving up an Incline.
Follow the link: Example 2.64.
28. Constant Deceleration of a Skater.
Follow the link: Example 2.65.
29. Constant Acceleration on an Inclined Plane.
Follow the link: Example 2.66.
30. Predicting the Final Velocity in a Constant Acceleration Motion.
Follow the link: Example 2.61.
31. Modeling a Varying Acceleration by Average Constant Acceleration.
Follow the link: Example 2.67.
32. Practice with a Friend: A Car Speeding Up a Ramp.
Follow the link: Exercise 2.7.1.
33. Practice with a Friend: A Skier Racing Down a Hill.
Follow the link: Exercise 2.7.2.
Freely Falling Motion
34. Freely Falling Vertical Motion of a Ball.
Follow the link: Example 2.70.
35. Flight Time to Reach the Top of a Vertical Trajectory.
Follow the link: Example 2.71.
36. Vertical Motion with a Turn Around in the Trajectory.
Follow the link: Example 2.72.
37. Falling Rock by a Window - Find Initial and Final Velocities.
Follow the link: Example 2.74.
Miscellaneous
38. Two Runners in a Race - Relative Motion.
Karl and Justin are in a \(10\text{-km}\) race. Karl runs at a constant speed of \(12\text{ km/h}\) and Justin at \(11.5\text{ km/h}\text{.}\) You can assume \(t = 0 \) at the start and their speeds are their full values at the start.
(a) Who will finish the race first?
(b) What is the value of time, \(t \text{,}\) when Karl finishes?
(c) What is the value of time, \(t \text{,}\) when Justin finishes?
(d) If Karl finishes first, how far away from the finish is Justin when Karl crosses the finish line, and if Justin finishes first, same question for Karl.
(e) How far apart are the two runners after \(12\text{ min} \text{?}\)
Hint.
(a) Think who is faster? (b) Use \(v = d/t\text{.}\) (c) Same as (b). (d) Use \(d = v t\) on slower with \(t\) the finish time of the faster. (e) Multiply the difference in their speeds by time.
Answer.
(a) Karl, (b) \(50\text{ min}\text{,}\) (c) \(52.2\text{ min}\text{,}\) (d) \(0.417\text{ km}\text{,}\) (e) \(100\text{ m}\text{.}\)
Solution 1. (a)
(a) Since Karl’s speed is greater, he will finish first.
Solution 2. (b)
(b) Using \(v = d/t \) on Karl gives
\begin{equation*}
t = \dfrac{d}{v} = \dfrac{10}{12}\text{ hr} = 50\text{ min}.
\end{equation*}
Solution 3. (c)
(c) Using \(v = d/t \) on Justin gives
\begin{equation*}
t = \dfrac{d}{v} = \dfrac{10}{11.5}\text{ hr} = 52.2\text{ min}.
\end{equation*}
Solution 4. (d)
(d) Since Karl finishes at \(t= 50\text{ min} \text{,}\) Justin will have covered the following distance by then (note: I need to convert \(50\text{ min} = 5/6\text{ hr} \) since the speed is given in per \(\text{hr}\) unit.)
\begin{equation*}
d = vt = 11.5\times \dfrac{5}{6} = 9.583\text{ km}.
\end{equation*}
That means, the remaining distance is
\begin{equation*}
10 - 9.583 = 0.417\text{ km}.
\end{equation*}
Solution 5. (e)
(e) Using \(d = v t \) with \(v\) being the difference of the two speeds. Also, since the speeds have time in \(\text{hr}\text{,}\) we need to convert \(t\) to \(\text{hr} \) as well.
\begin{equation*}
d = (12-11.5)\times \dfrac{12}{60} = 0.1\text{ km} = 100\text{ m}.
\end{equation*}
You can also do this part by first finding how far Karl and Justin went, and then subtracting their distances.
39. Acceleration and Displacement for a Cheetah from Speed Versus Time Plot.
Cheetah are ferrocious animals with very high top speeds. The figure below shows the speed of a cheetah with time. You can assume the motion is towards the positive \(x \) axis, then the ordinate in the plot will be \(v_x \) with abscissa \(t\) shown in Figure 2.81.
(a) Estimate how far cheetah goes in first \(30 \) seconds.
(b) Estimate acceleration of cheetah at the following instants: (i) \(t = 0\text{,}\) (ii) \(t = 5\text{ sec}\text{,}\) (iii) \(t = 17.5\text{ sec}\text{,}\) and (iv) \(t = 30\text{ sec}\text{.}\) At each instant, indicate both the magnitude and direction of the acceleration.
If you are curious about Cheetahs, see this Houston Zoo Video on the Youtube.
2
youtu.be/7t_OysaqHRcHint 1. (a)
(a) You can approximate the area of interest as made up areas of triangles and rectangles.
Hint 2. (b)
(b) You can estimate instantaneous acceleration from the slope of the tangents.
Answer.
(a) \(975\text{ m}\text{,}\) (b) (i)\(13.33\text{ m/s}^2\text{,}\) (ii) \(2.82\text{ m/s}^2\text{,}\) (iii) \(0 \text{,}\) (iv) \(-2.44\text{ m/s}^2\text{.}\)
Solution 1. (a)
(a) Our answers will differ since we may break up the area between \(t=0\) and \(t=30\text{ sec}\) in different ways. My area will come from the areas shaded in Figure 2.82.
The areas sum up to
\begin{align*}
\text{triangles } \amp +\text{ rectangles} = \\
\amp (75+50+50) + (750+50) = 975\text{ m}.
\end{align*}
Solution 2. (b)
(b) Our answers will differ since we may draw tangents a little differently. Figure 2.83 contains the tangents at the four instants.
The slopes of these tangents give the acceleration at the corresponding instants.
\begin{align*}
\amp \text{(i)}\ \ a_x(\text{at }0) = \dfrac{40-0}{3-0} = 13.33\text{ m/s}^2, \\
\amp \text{(ii)}\ \ a_x(\text{at }5) = \dfrac{40-16}{8.5-0} = 2.82\text{ m/s}^2, \\
\amp \text{(iii)}\ \ a_x(\text{at }17.5) = 0, \\
\amp \text{(iv)}\ \ a_x(\text{at }30) = \dfrac{18-40}{35-26} = -2.44\text{ m/s}^2.
\end{align*}
The value at \(t= 30\text{ sec}\) is negative because the cheetah, while moving towards positive \(x \) axis, is slowing down.
40. Motion of a Train Between Stations.
Figure 2.84 shows speed of a train between two stations. Assume a straight track between the two stations.
(a) What is the distance between the two stations?
(b) Supposing \(x \) axis is pointed from A towards B, plot the acceleration \(a_x \) versus \(t \text{.}\)
(c) Using your acceleraiton values, find the distance travelled in the three durations (i) from \(0 \) to \(t = 2\text{ sec} \text{,}\) (ii) from \(t = 2\text{ sec} \)to \(t = 5\text{ sec} \text{,}\) and (iii) from \(t = 5\text{ sec} \)to \(t = 6\text{ sec} \text{.}\) Verify that your answer to this part agrees with your answer to part (a)
Hint.
(a) Area under the curve, (b) Slopes, (c) Use constant acceleration in the three segments.
Answer.
(a) \(10,800\text{ m}\text{,}\) (b) three acceleration values \(\dfrac{1}{3}\text{ m/s}^2\text{,}\) \(0\text{,}\) \(-\dfrac{2}{3}\text{ m/s}^2\text{,}\) (c) \(2400\text{ m} + 7200\text{ m} + 1200\text{ m} = 10,800\text{ m}\text{.}\)
Solution 1. (a)
(a) Since the motion does not have a turn around in direciton, the speed plot is same as velocity plot. Therefore, we can get the distance traveled by area-under-the-curve. We also convert the time into seconds.
\begin{equation*}
d = \dfrac{1}{2}\times 120\times 40 + 180\times 40 + \dfrac{1}{2}\times 60\times 40 = 10,800\text{ m}.
\end{equation*}
Solution 2. (b)
(b) From the slopes we find three values of accelerations.
\begin{align*}
\amp a_{i,x} = \dfrac{40}{120} = \dfrac{1}{3}\text{ m/s}^2, \\
\amp a_{ii,x} = 0, \\
\amp a_{iii,x} = \dfrac{-40}{60} = -\dfrac{2}{3}\text{ m/s}^2.
\end{align*}
We plot these in Figure 2.85.
Solution 3. (c)
(c) (i) With \(a_{x} = \dfrac{1}{3}\text{ m/s}^2\text{,}\) \(v_{i,x}=0\text{,}\) and \(\Delta t = 120\text{ sec}\text{,}\) we get
\begin{equation*}
\Delta x_1 = 0 + \dfrac{1}{2}\times \dfrac{1}{3} \times 120^2 = 2400\text{ m}.
\end{equation*}
(ii) This is a constant velocity motion.
\begin{equation*}
\Delta x_2 = v_2 \Delta t = 40\times 180 = 7200\text{ m}.
\end{equation*}
(iii) Finally, in this part, we have \(a_{x} = -\dfrac{2}{3}\text{ m/s}^2\text{,}\) \(v_{i,x}=40\text{ m/s}\text{,}\) and \(\Delta t = 60\text{ sec}\text{.}\) These give us
\begin{equation*}
\Delta x_3 = 40\times 60 - \dfrac{1}{2}\times \dfrac{2}{3} \times 60^2 = 1200\text{ m}.
\end{equation*}
Therefore, the total
\begin{equation*}
\Delta x = 2400 + 7200 + 1200 = 10,800\text{ m}.
\end{equation*}
41. Two Stones Thrown Vertically at Different Times Reaching Ground at the Same Time.
Two stones are dropped from the roof of a \(50\text{-m}\) tall building. The first stone is released smoothly from rest, and after \(0.5\text{ sec}\) later, the second stone is thrown vertically down with an intial speed such that they reach the ground at the same time.
(a) With what initial speed was the second stone thrown?
(b) With what speed did the first stone hit the ground?
(c) With what speed did the second stone hit the ground?
Hint.
Both stones follown free fall motion related in time by \(t_1 = t_2 + 0.5 \text{.}\) Set up two sets of equations, one for each stone and solve them simultaneously.
Answer.
(a) \(5.29\text{ m/s} \text{,}\) (b) \(31.4\text{ m/s}\text{,}\) (c) \(31.78\text{ m/s} \text{.}\)
Solution. (a),(b),(c)
(a), (b) , (c), all three parts can be solved by setting up two sets of equations, one set for each stone, and relation \(t_1 = t_2 + 0.5 \) for the times of the two stones. Let us use positive \(y\) axis up to keep track of signs with origin at the place the motions started. That will make \(y_i = 0\) and \(y_f = -50 \text{ m}\text{.}\) Let us use subscript 1 for stone 1 and 2 for stone 2, and drop \(y\) from subscripts.
For stone 1, we have the following two equations.
\begin{align}
-50 \amp = 0 - \dfrac{1}{2}\, 9.81\, t_1^2,\tag{2.33}\\
v_{1f} \amp= 0 - 9.81\, t_1,\tag{2.34}
\end{align}
For stone 2, we have the following two equations.
\begin{align}
-50 \amp= v_{2i}\, t_2 - \dfrac{1}{2}\, 9.81\, t_2^2,\tag{2.35}\\
v_{2f} \amp = v_{2i} - 9.81\, t_2,\tag{2.36}
\end{align}
with
\begin{equation*}
t_2 = t_1 - 0.5.
\end{equation*}
From Eq. (2.33), we solve for \(t_1\) and keep the positive root as our answer.
\begin{equation*}
t_1 = 3.2\text{ sec}.
\end{equation*}
Therefore,
\begin{equation*}
t_2 = 2.7\text{ sec}.
\end{equation*}
Using \(t_1\) in Eq. (2.34) give,
\begin{equation*}
v_{1f} = - 9.81 \times 3.2 = -31.4\text{ m/s}.
\end{equation*}
Using \(t_2\) in Eq. (2.35) gives
\begin{equation*}
v_{2i} = \dfrac{-50 + 4.9 \times 2.7^2 } { 2.7 } = -5.29\text{ m/s}.
\end{equation*}
\begin{equation*}
v_{2f} = -5.29 - 9.81 \times 2.7 = -31.78\text{ m/s}.
\end{equation*}
42. Tennis Balls Launched Vertically at Different Times.
Two balls are launched straight up at different times from a tennis ball launching machine. The second ball is launched at the time the first ball is at the top of its flight. If the launching speed of the balls are \(20\text{ m/s}\text{,}\) (a) where would the two balls hit each other and (b) what will be the time when they hit the ball if \(t=0\) at the instant of the launch of the second ball? Assume the effect of the air resistance to be negligible on the motion.
Hint.
First find the height the first ball will fly before falling back.
Answer.
(a) \(15.3\text{ m}\text{,}\) (b) \(1.02\text{ s}\text{.}\)
Solution. (a),(b)
Let \(y=0\) at the launch point with positive \(y\) axis pointed up. The first ball reaches \(y=h\) before falling with
\begin{equation*}
y = h = \dfrac{-v_i^2}{2g} = \dfrac{-20^2}{2\times 9.81} = 20.39\text{ m}.
\end{equation*}
Now, ball 1 moves in the negative \(y\) direction at \(t=0\) starting at \(y_{1i}=20.39\text{ m}\) with \(v_{1i}=0\) and ball 2 moves in the positive \(y\) direction \(y_{2i}=0\) starting with \(v_{2i}=20\text{ m/s}\text{.}\) We want \(y\) where they hit each other, i.e., \(y_{1f} = y_{2f} = y\text{.}\) Let \(t\) be the duration since ball 2 was launched. For the two equations we get
\begin{gather*}
\text{ ball 1: } y - 20.39 = - \dfrac{1}{2}\times 9.81\, t^2\\
\text{ ball 2: } y = 20\, t - \dfrac{1}{2}\times 9.81\, t^2
\end{gather*}
Subtracting first equation from the second we get
\begin{equation*}
20.39 = 20\, t\ \ \Longrightarrow\ \ t = 1.02\text{ s}.
\end{equation*}
Using this \(t\) we get
\begin{equation*}
y = 20.39 - \dfrac{1}{2}\times 9.81\times 1.02^2 = 15.3\text{ m}.
\end{equation*}
43. Motion with Two Constant Acceleration Segments.
A hockey puck is shot at \(40\text{ m/s}\text{.}\) Initially, the puck decelerates at \(3\text{ m/s}^2\text{,}\) but after \(50\text{ m}\text{,}\) the puck runs into a rough patch, where the puck has constant deceleration \(12\text{ m/s}^2\) and comes to rest.
(a) How far from the initial place does the puck come to rest?
(b) How much time did it take for the puck to come to rest?
Hint.
You will need to set up two sets of equations with final velocity of segment 1 is equal to the initial velocity of segment 2.
Answer.
(a) \(104.3\text{ m}\text{,}\) (b) \(4.31\text{ sec} \)
Solution. (a),(b)
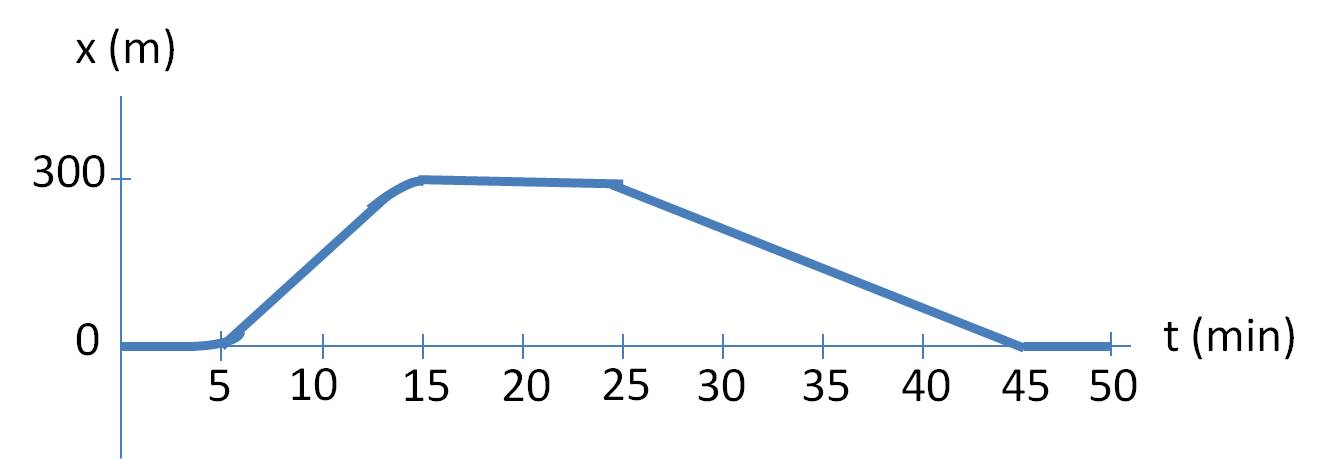
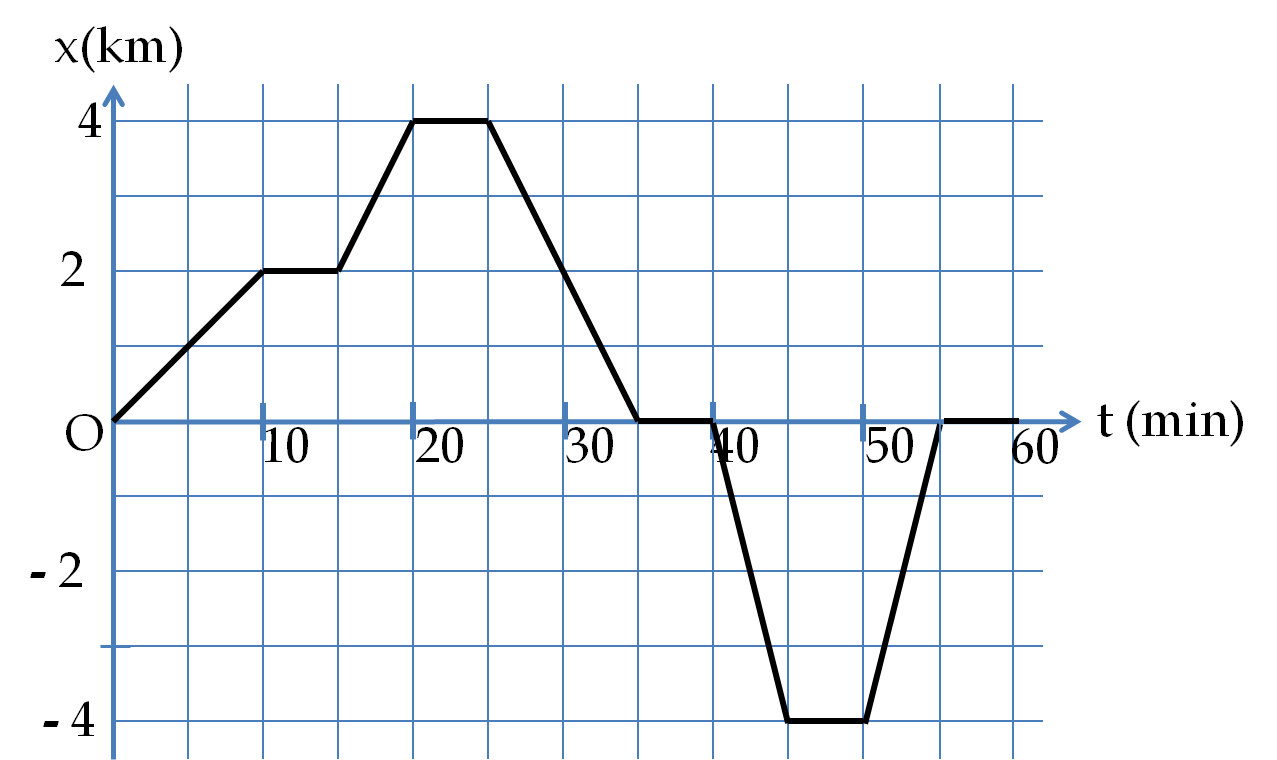
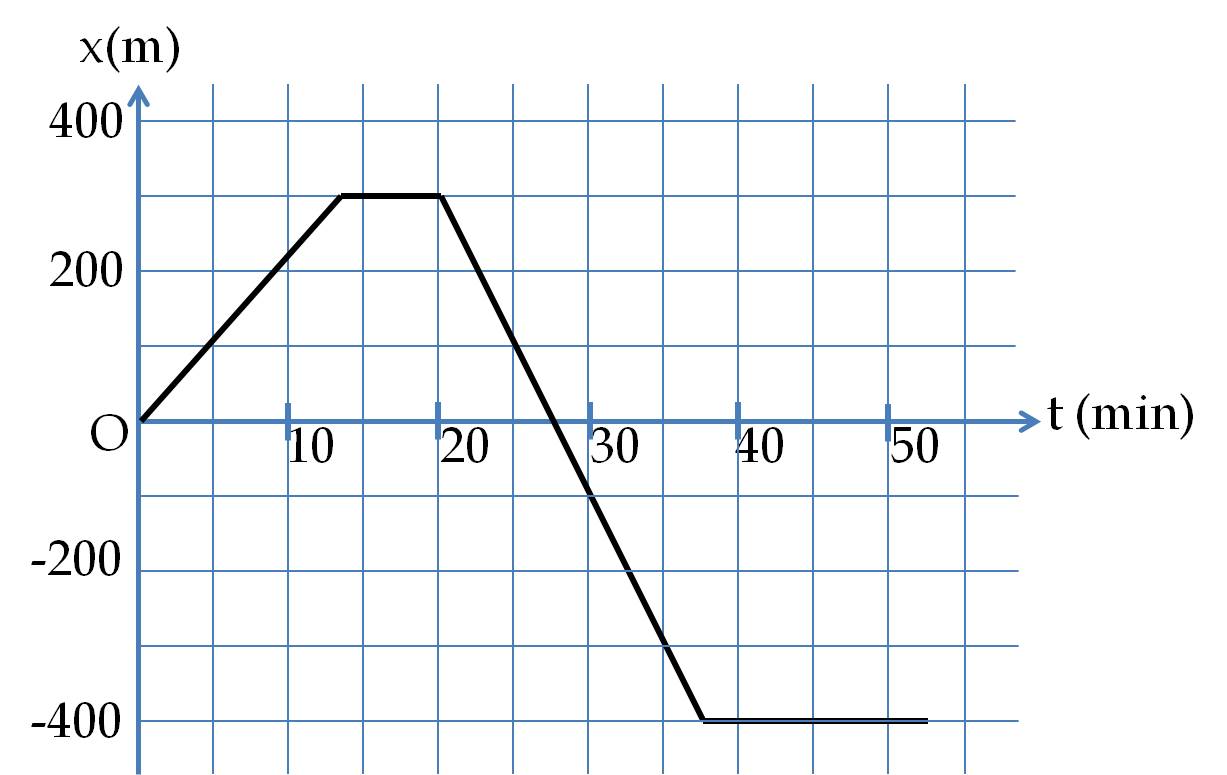
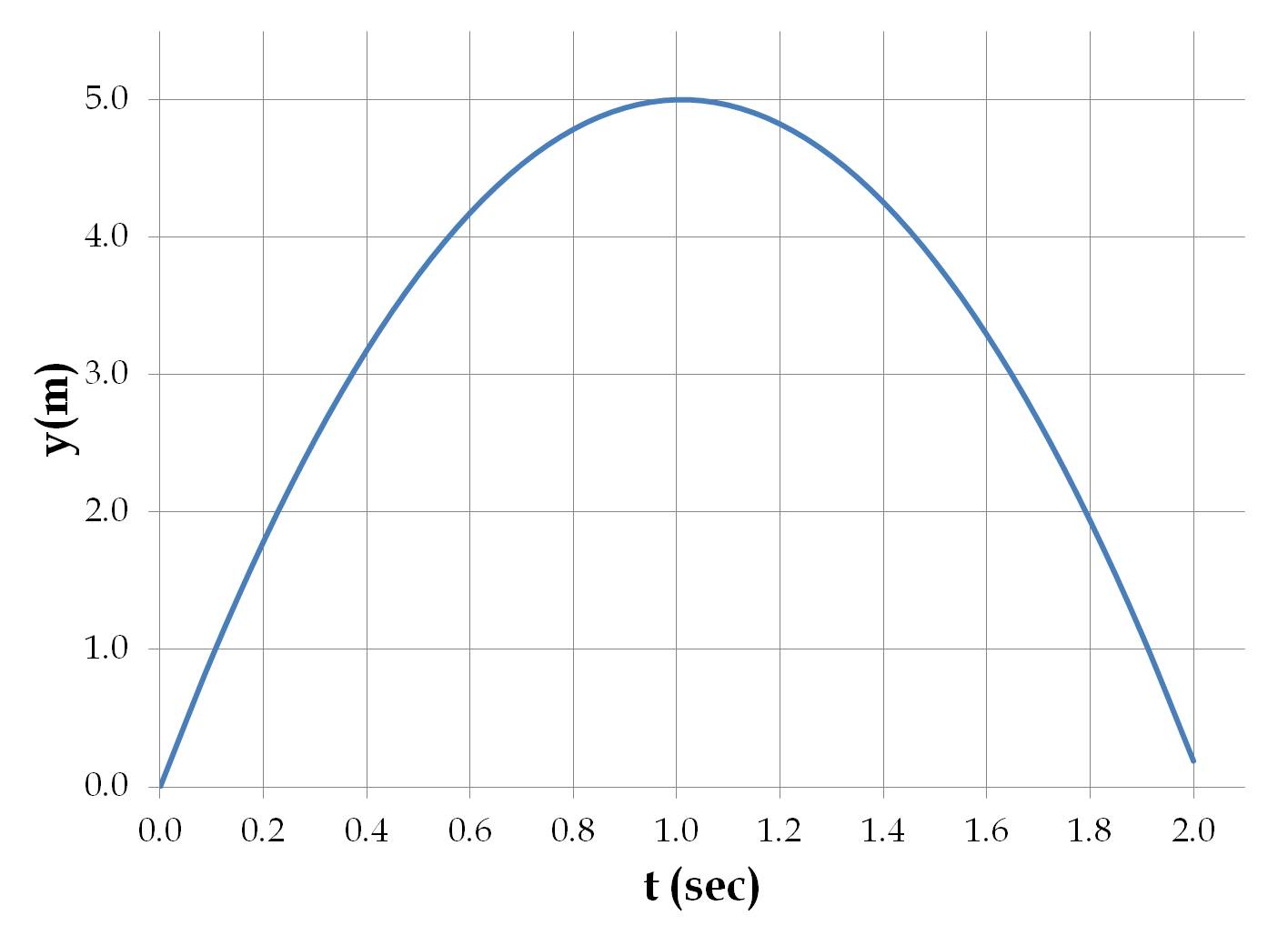
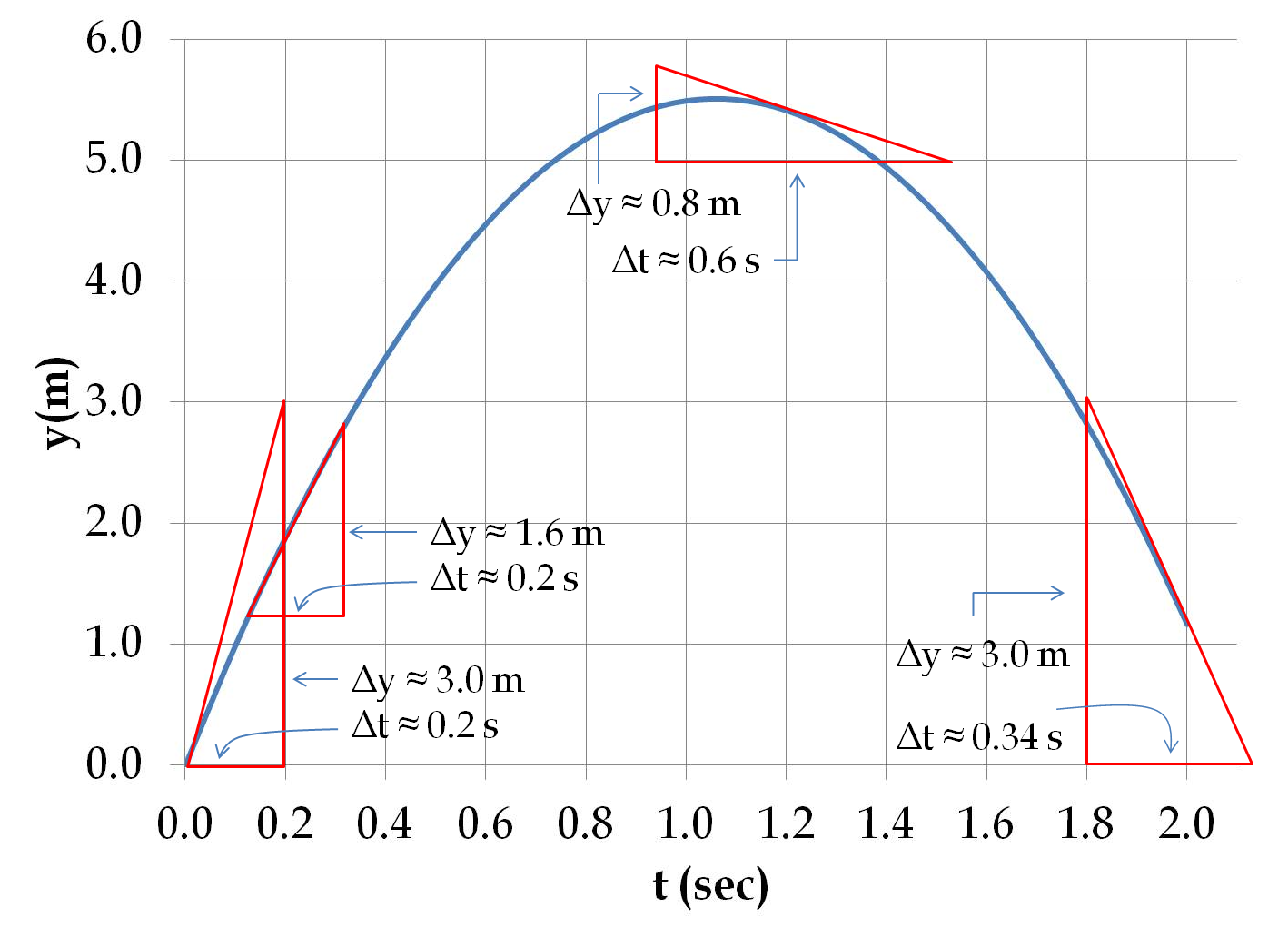
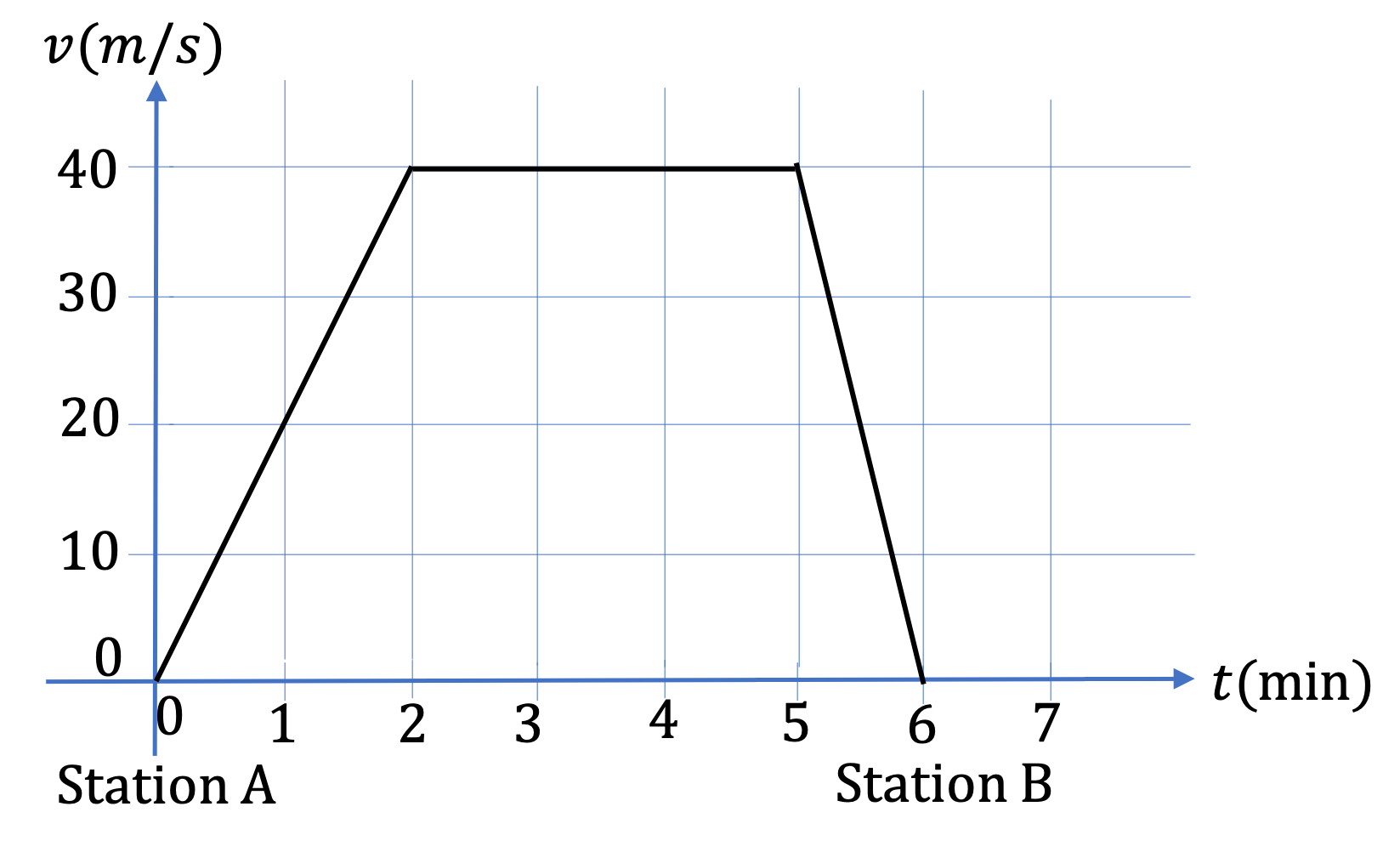
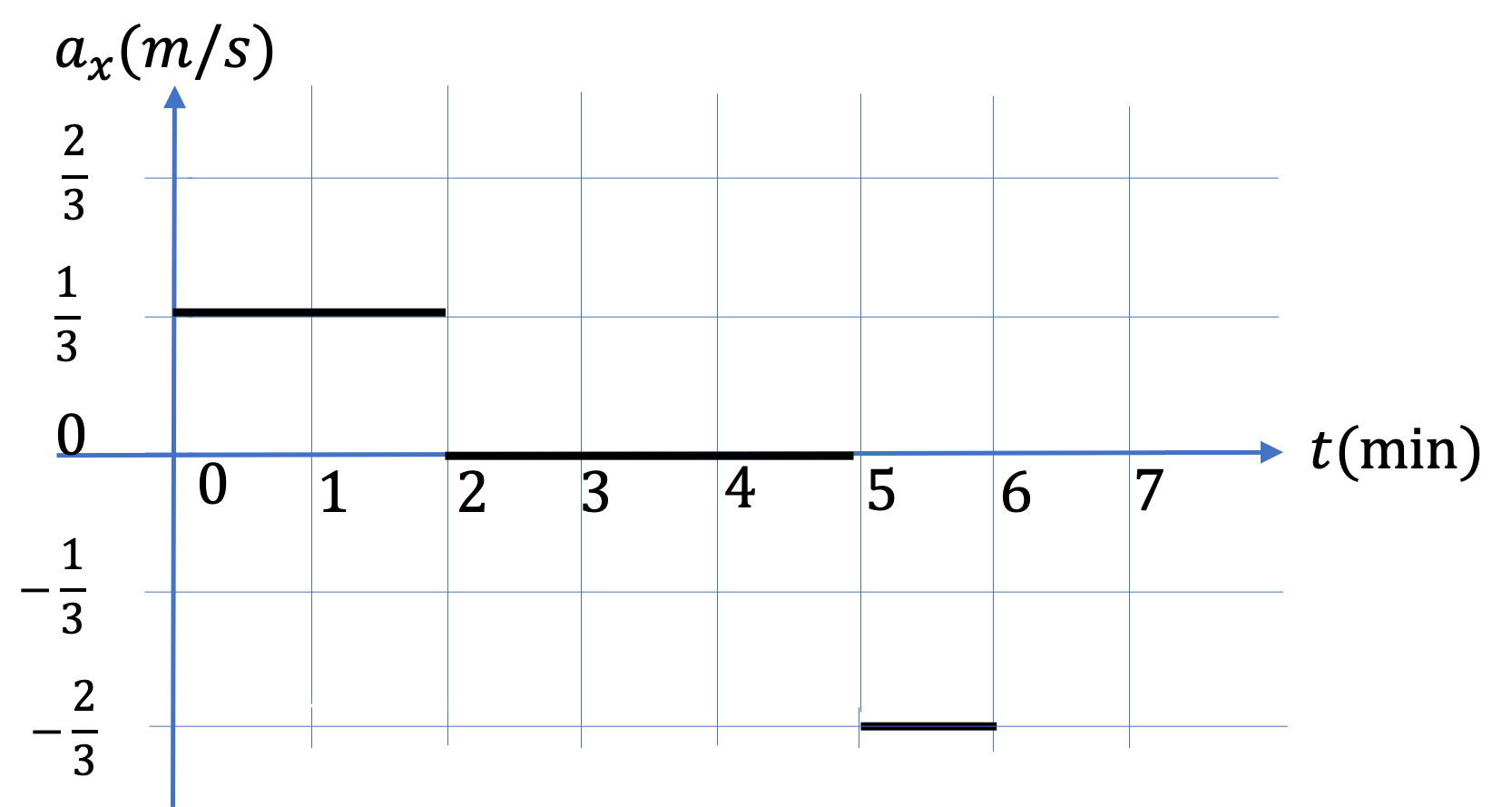
(a) and (b):
There are two constant-acceleration segments in this problem, such that final velocity and final position of the first segment is the initial velocity and initial position of the second segment. Let us denote the quantities of the first and second segments by subscripts 1 and 2, respectively.
We point positive \(x \) axis from the initial point of the first segment towards the final point where the puck comes to rest. Using this coordinate system, we have the following knowns and unknowns for segment 1.
First Segment:
Suppressing units in calculations, we list knowns and unknowns.
\begin{align*}
\amp a_1 = - 3,\ \ t_1 = ?, \\
\amp x_{1,i} = 0,\ \ v_{1,i} = 40,\ \ x_{1,f} = 50,\ \ v_{1,f} = ?,
\end{align*}
The equation \(v_f^2 = v_i^2 + 2 a x \) gives
\begin{equation*}
v_{1,f}^2 = 40^2 + 2 \times (-3) \times 50 = 1600 - 300 = 1300.
\end{equation*}
This gives
\begin{equation*}
v_{1,f} = \pm 36.1\text{ m/s}.
\end{equation*}
Since the puck is moving in the same direction as the direction of the positive \(x \) axis, the positive root is the right choice here.
\begin{equation*}
v_{1,f} = + 36.1\text{ m/s}.
\end{equation*}
Now, using \(v_f = v_i + a t\text{,}\) we get
\begin{equation*}
t = \dfrac{v_f - v_i}{a} = \dfrac{36.1 - 40}{-3} = 1.3\text{ sec}.
\end{equation*}
Second Segment:
Let us use \(t_2 \) for \(t_{2,f} - t_{2,i}\) and place another origin at \(x_{2,i}\text{.}\)
\begin{align*}
\amp a_2 = - 12,\ \ t_2 = ?, \\
\amp x_{2,i} = 0,\ \ v_{2,i} = 36.1,\ \ x_{2,f} = ?,\ \ v_{2,f} = 0,
\end{align*}
Using \(v_f = v_i + a t\text{,}\) we get \(t\)
\begin{equation*}
t_2 = \dfrac{v_{2,f} - v_{2,i}}{a_2} = \dfrac{0 - 36.1}{-12} = 3.01\text{ sec}.
\end{equation*}
Using \(x = v_i t +\dfrac{1}{2}at^2\text{,}\) we get
\begin{equation*}
x_{2,f} = 36.1\times 3.01 +\dfrac{1}{2}\times(-12) \times 3.01^2 = 54.3\text{ m}.
\end{equation*}
(a) The total distance is \(50 + 54.3 = 104.3\text{ m}\text{.}\)
(b) The total time is
\begin{equation*}
t_1 + t_2 = 1.3 + 3.01 = 4.31\text{ sec}.
\end{equation*}
44. (Calculus) Varying Acceleration During Parachute Jump.
A parachuter drops off an air plane with zero vertical speed. Suppose magnitude of acceleration of the parachuter varies linearly in time, from \(g \) at \(t=0\) to zero at \(t=\tau \text{.}\)
(a) What is the speed at an arbitrary instant \(t \) before the acceleration is zero?
(b) What is the speed at the instant \(\tau \text{?}\)
(c) How far has he fallen in time \(\tau \text{?}\)
Hint.
(a) Integrate \(a_y\text{.}\) (b) Evaluate at \(t = \tau\) . (c) Integrate \(v_y\text{.}\)
Answer.
(a) \(\dfrac{g}{2\tau}\, t^2 - g t \text{,}\) (b) \(\dfrac{1}{2} g\tau\text{,}\) (c) \(\dfrac{1}{3}\,g \tau^2\text{.}\)
Solution 1. (a)
(a) We would find velocity by integrating the acceleration, and then get the speed from the absolute value. The magnitude of acceleration drops from \(g \) to zero in time \(\tau\text{.}\) Therefore, we have the following formula for the magnitude of the acceleration at instant \(t\text{.}\)
\begin{equation*}
a(t) =
\begin{cases}
\dfrac{g}{\tau}\, |\tau - t| \amp t \le \tau\\
0 \amp t \gt \tau
\end{cases}
\end{equation*}
Let positive \(y \) axis be pointed up so that
\begin{equation*}
a_y(t) =
\begin{cases}
\frac{g}{\tau} t - g \amp t \le \tau\\
0 \amp t \gt \tau
\end{cases}
\end{equation*}
Now, we integrate this from \(t = 0\) to \(t=t\text{.}\) With \(v_y=0\) at \(t = 0\text{.}\)
\begin{equation}
v_y(t) - 0 = \int_0^{t} a_y(t)\, dt = -\dfrac{g}{2\tau}\, t^2 - g t.\tag{2.37}
\end{equation}
Therefore, speed at arbitrary instant is
\begin{equation*}
v = |\dfrac{g}{2\tau}\, t^2 - g t|.
\end{equation*}
Solution 2. (b)
(b) Speed at instant \(\tau\) will be obtained by setting \(t= \tau\) in the answer for part (a) and taking the absolute value.
\begin{equation*}
v = \dfrac{1}{2} g\tau.
\end{equation*}
Solution 3. (c)
(c) Integrating \(v_y(t) \) will give \(\Delta y\text{.}\)
\begin{equation*}
y(t) - 0 = \int_0^{\tau} v_y(t)\, dt = -\dfrac{g}{6\tau}\, \tau^3 -\dfrac{1}{2}g \tau^2 = -\dfrac{1}{3}\,g \tau^2.
\end{equation*}
The magnitude of this gives the distance fallen.
\begin{equation*}
h = |y(t)| = \dfrac{1}{3}\,g \tau^2.
\end{equation*}
45. (Calculus) Varying Acceleration and Terminal Speed.
Consider an object falling vertically. In a coordinate system with the positive \(y \) axis pointed down, the acceleration \(a_y\) has the following expression. Let \(y=0\) at \(t=0\text{.}\)
\begin{equation*}
a_y = g - \gamma v_y,
\end{equation*}
where \(g \) is acceleration due to gravity, and \(\gamma \) is a constant, called the damping constant.
(a) Show that at the instant the acceleration is zero, the speed is
\begin{equation*}
v = \dfrac{g}{\gamma}.
\end{equation*}
The speed is called the terminal speed. We will denote it by \(v_T \text{.}\)
(b) Prove that velocity at arbitrary instant \(t \) is given by
\begin{equation*}
v_y = v_T\left( 1 - e^{-\gamma\, t} \right).
\end{equation*}
(c) Prove that the \(y \) coordinate at arbitrary instant \(t \) is given by
\begin{equation*}
y = v_T\, t - \dfrac{v_T}{\gamma}\left( 1 - e^{-\gamma\, t} \right).
\end{equation*}
Hint.
(a) Set \(a_y=0\text{.}\) (b) Write \(a_y = dv_y/dt\text{,}\) then change variable to \(k = -\gamma v_y + g \) and integrate. (c) Integrate \(v_y\text{.}\)
Answer.
Already given in problem statement.
Solution 1. (a)
(a) Setting \(a_y=0\) and \(v_y = v_T \text{,}\) we imediately get the answer.
\begin{equation*}
v_T = \dfrac{g}{\gamma}.
\end{equation*}
Solution 2. (b)
(b) We express \(a_y = dv_y/dt\) and rearrange to obtain
\begin{equation*}
\dfrac{dv_y}{g - \gamma v_y} = dt.
\end{equation*}
Integrating this from \(t=0\) to \(t =t\) with \(v_y(0)=0\) and \(v_y(t)=v_y\text{,}\) we get
\begin{equation*}
\ln\left( \dfrac{| g - \gamma v_y|}{g} \right) = -\gamma t.
\end{equation*}
Since \(g\) is larger than \(\gamma v_y \text{,}\) exponentiating and then rearranging gives.
\begin{equation*}
v_y = \dfrac{g}{\gamma} \left( 1 - e^{-\gamma t}\right),
\end{equation*}
which is
\begin{equation*}
v_y = v_T\left( 1 - e^{-\gamma\, t} \right).
\end{equation*}
Solution 3. (c)
(c) Integrating \(v_y\) gives the desired answer.
\begin{equation*}
\int dy = \int v_y dt.
\end{equation*}
Use \(v_y \) from (b) and carry out the integration.
\begin{equation*}
y = v_T\, t - \dfrac{v_T}{\gamma}\left( 1 - e^{-\gamma\, t} \right).
\end{equation*}
46. Practice with a Friend: Variable Acceleration.
A runner runs on a straight track. Starting from rest, the runner runs for \(10\text{ sec}\) at a constant acceleration of \(0.4\text{ m/s}^2\text{,}\) then he decreases his acceleration to \(0.2\text{ m/s}^2\) for another \(12\text{ sec}\text{.}\) After that, he coasts for \(38\text{ sec}\) at the final speed. How far has he gone from the starting place?
47. (Calculus) Practice with a Friend: Find Distance from Acceleration Given as a Function of Time.
A car’s acceleration changes with time according to
\begin{equation*}
a(t) = 5.0\left( 1 - e^{-0.2\, t} \right).
\end{equation*}
Here unit of acceleration is \(\text{m/s}^2\text{.}\) Starting from rest at \(t=0\text{,}\) how far will the car go in \(5.0\text{ sec}\text{?}\)
48. Practice with a Friend: Ball Tossed up on an Unknown Planet.
A ball is tossed straight up on an unknown planet with an unknown speed and round trip times (ACA and BCB) at two different heights marked A and B in Figure 2.86 are observed.
With height \(H = 2\text{ m}\) between A and B, return times observed are \((ACA) = 2.8\text{ sec}\) and \((BCB) = 2.0\text{ sec}\text{.}\) From this data, find the value of \(g\text{.}\) (Don’t assume \(g=9.81\text{ m/s}^2\text{.}\))
49. Practice with a Friend: Ant Moving Half Distance In Same Time.
An ant is moving in a straight line with a variable speed. It covers the first meter in \(5\) sec, the next \(0.5\) m in \(5\) sec, the next \(0.25\) m also in \(5\) sec, and so on. That is, it covers \(\frac{1}{2}\) of the previous step in same amount of time as the last step. (a) How much distance would it travel in all? (b) How much time the ant takes to get to the final place? (c) What is the average speed of the ant?
Answer.
(a) \(2\) m; (b) \(\infty\) ; (c) \(0\text{.}\)
50. Practice with a Friend: Ultrasound Imaging from Reflection Times of the Wave.
Ultrasound imaging is based on echoes of ultrasound pulses from the reflectors in the tissue. In a particular experiment \(3.0\,\mu\text{s}\) apart echoes are heard when an ultrasound pulse if sent into the tissue. How far apart are the reflectors? Assume ultrasound travels with a speed of \(1500\,\text{m/s}\text{.}\)
Hint.
Ultrasound must go to the farthest one and return in the given time.
Answer.
\(2.25\,\text{mm}\text{.}\)
51. Practice with a Friend: Packages to be Dropped in Bins Moving on a Conveyor.
Packages from a height of \(3\,\text{m}\) are to be dropped in equally spaced bins moving at a constant speed on a conveyor belt. How fast the conveyor belt must move if the bins are \(2\,\text{m}\) apart so that packages land at the center each time?
Answer.
\(2.56\,\text{m/s}\text{.}\)
52. Practice with a Friend: An Insect Flying Between Two Moving Walls.
An insect flies at a constant speed between two moving walls that are initially a distance \(D\) meters apart and insect being near one wall. The insect goes from one wall to the other and back without losing anytime in the turn around, and does this continuously. If both the walls move right with a constant speed \(u\, (\text{m/s})\) with respect to the floor and the inssect’s speed is \(s (\text{m/s})\text{,}\) then find the distance the insect has traveled by the \(N^\text{th}\) turn. Assume that at \(t= 0\) the insect is moving to the right from its position just to the right of the left wall.
