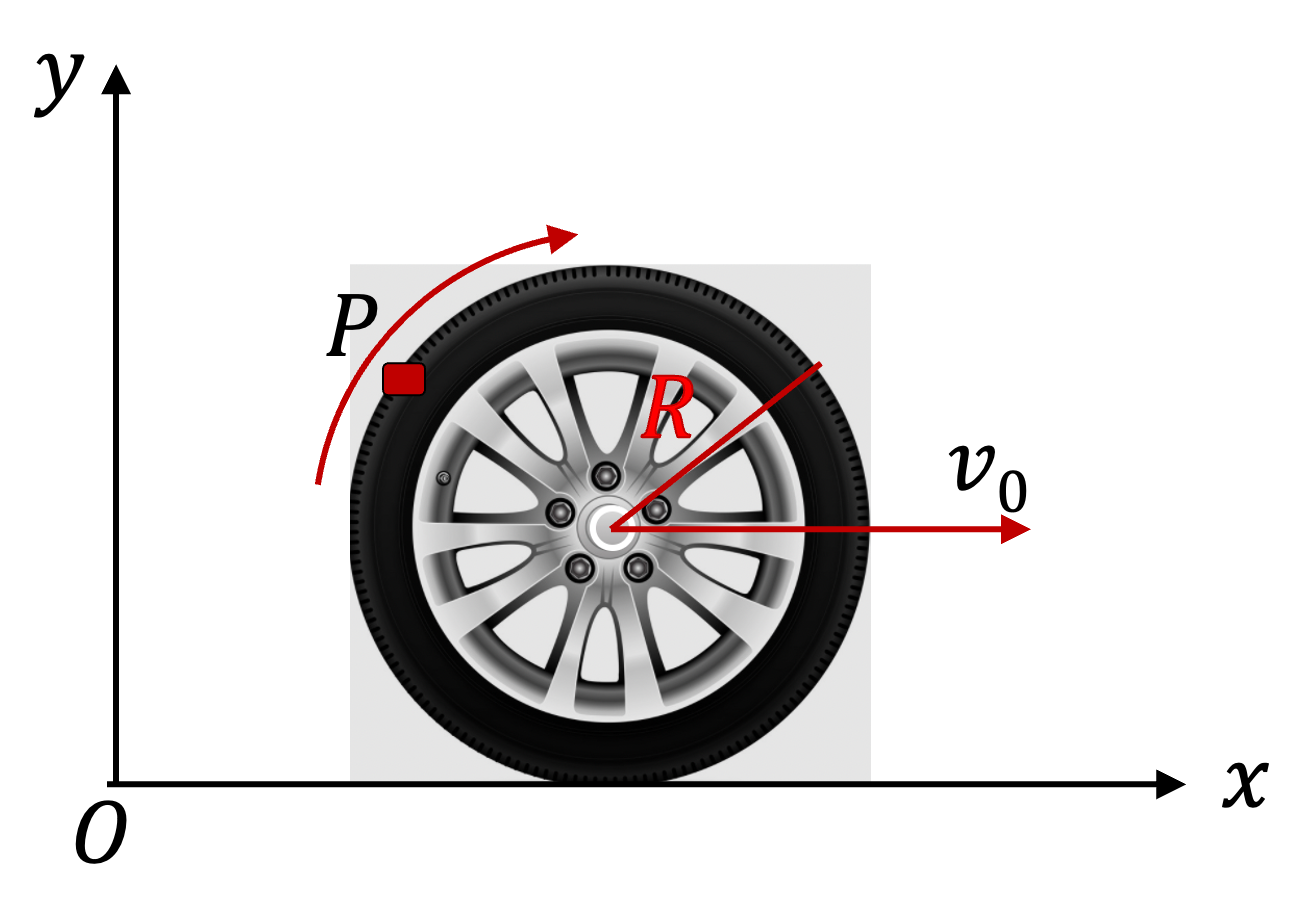
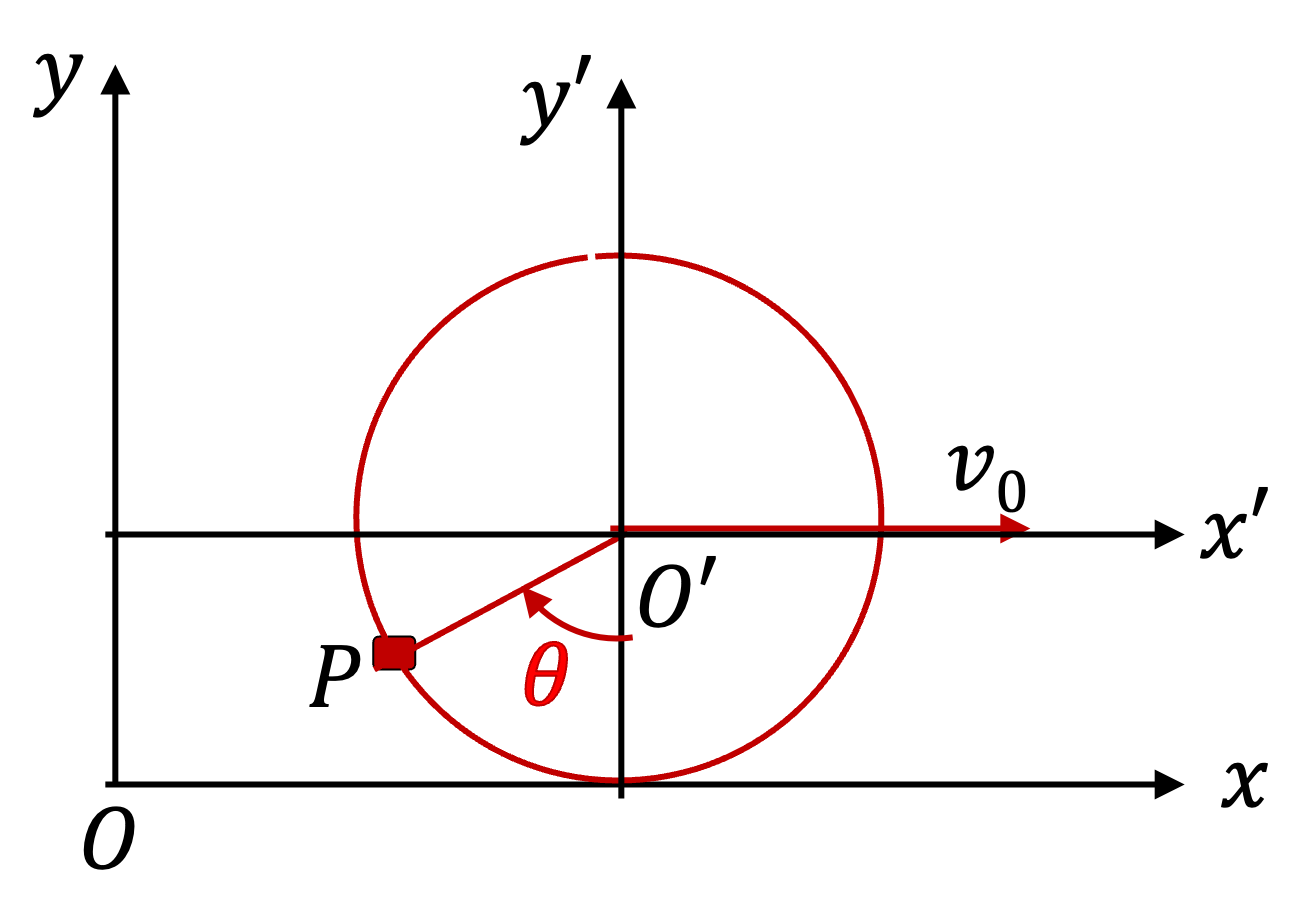
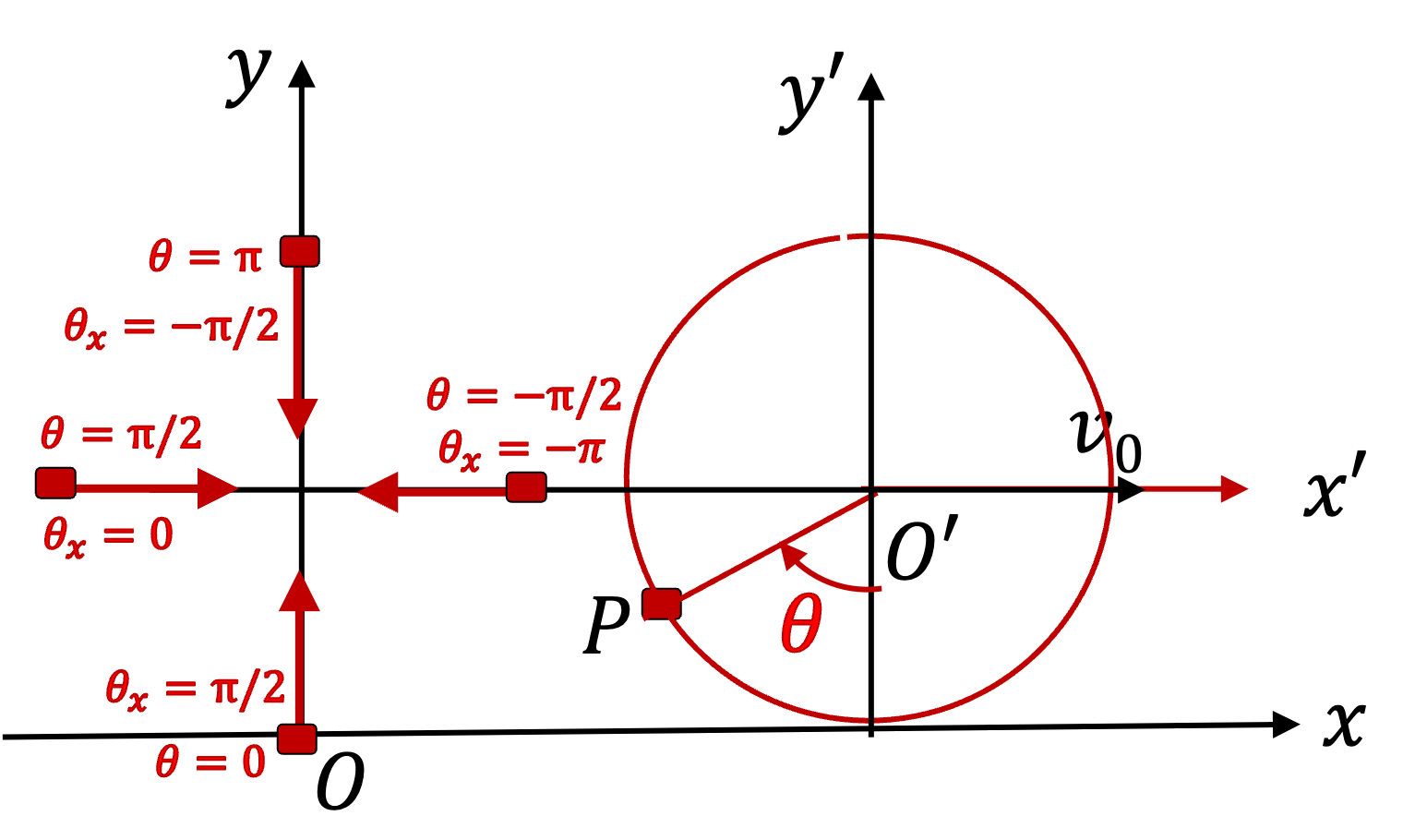
Now, that we know the components of position, we can obtain components of velocity by taking derivatives. Thus,
\begin{align*}
\amp v_x = \frac{dx}{dt} = (-R\cos\theta)\frac{d\theta}{dt} + v_0 \\
\amp v_y = \frac{dy}{dt} = (-R\sin\theta)\frac{d\theta}{dt}
\end{align*}
Since the tire is not slipping, the rate at which angle \(\theta\) changes is related to the speed with which center of the tire is moving. The tire has rotated by \(R\Delta\theta\text{,}\) its center has moved \(v_0\Delta t\text{.}\) Equating them we get
\begin{equation*}
R\Delta\theta = v_0\Delta t.
\end{equation*}
This gives
\begin{equation*}
\frac{d\theta}{dt} = \frac{v_0}{R}.
\end{equation*}
Using this, we rewrite the components of velocity as
\begin{align*}
\amp v_x = (1 -\cos\theta)\;v_0 \\
\amp v_y = (-\sin\theta)v_0.
\end{align*}
Therefore, magnitude of velocity, i.e., speed is
\begin{equation*}
v = \sqrt{v_x^2 + v_y^2} = v_0\sqrt{ 2 - 2 \cos\theta} = 2 v_0 \left| \sin(\theta/2) \right|.
\end{equation*}
Note: this tells us that the speed of pebble when touching the ground is zero (since \(\theta=0\)) and when at the very top, it is \((2\;v_0)\) (since \(\theta=\pi\)). That is, speed of the pebble in \(Oxy\) coordinate system changes as it goes around.
The direction of velocity can again be given with respect to the \(x\) axis by using arctangent.
\begin{equation*}
\theta_x = \tan^{-1}(v_y/v_x) = \tan^{-1}\left( \frac{-\sin\theta}{1 -\cos\theta} \right).
\end{equation*}
You can further simplify this expression by using double angle formulas. Try that. You should be able to express this without arctangent operation.